【datawhale学习-强化学习】2.MDP+DP

---

基于蘑菇书easyRL以及joyRL，学习整理得到。

---

MP-MRP-MDP

马尔可夫过程MP$\to$ 马尔可夫奖励过程MRP $\to$ 马尔可夫决策过程
递进关系：马尔可夫过程描述了状态之间的转移，马尔可夫奖励过程引入了奖励，而马尔可夫决策过程则进一步考虑了决策者在每个状态下选择动作的问题。

1. 马尔可夫过程（Markov Process）:

马尔可夫过程（MP）是一种随机过程，其基本特性是具有马尔可夫性质，即未来的状态只依赖于当前状态，而与过去的状态无关。

对于离散时间的马尔可夫过程，其状态转移概率满足马尔可夫性质，即未来状态只依赖于当前状态：
$$P(X_{t+1}=x_{t+1}|X_t=x_t,X_{t-1}=x_{t-1},\dots ,X_0=x_0)=P(X_{t+1}=x_{t+1}|X_t=x_t)$$

连续时间的马尔可夫过程则使用概率密度函数。

2. 马尔可夫奖励过程（Markov Reward Process）:

马尔可夫奖励过程（MRP）是马尔可夫过程的扩展，引入了奖励的概念。在马尔可夫奖励过程中，每个状态转移都伴随着一个奖励，表示在从一个状态转移到另一个状态时所获得的即时回报。这样的模型常用于描述一个代理与环境的交互，其中代理根据当前状态的奖励来决定下一步的动作。

马尔可夫奖励过程是对马尔可夫过程的扩展，引入了奖励函数 $R$。在离散时间下，其定义为：
$$R_t=\mathbb{E}[R_{t+1}|X_t=x_t]$$

其中，$R_t$是在状态 $X_t$ 处获得的奖励，$\mathbb{E}$ 表示期望。

3. 马尔可夫决策过程（Markov Decision Process）:

马尔可夫决策过程（MDP）是马尔可夫奖励过程的一个进一步扩展，引入了决策者的概念。MDP是用于描述具有决策制定者（agent）和环境之间相互作用的数学框架。在MDP中，决策制定者在每个时刻根据当前状态选择一个动作，然后从环境中获得奖励，并转移到新的状态。MDP的目标是找到一个策略，即从状态到动作的映射，使得长期累积的奖励最大化。

马尔可夫决策过程包含状态空间 $S$、动作空间 $A$、状态转移概率 $P$、奖励函数 $R$ 和折扣因子 $\gamma$。

• 状态转移概率 $P$：表示在执行动作 $a$ 后，从状态 $s$ 转移到状态 $s^{\prime }$ 的概率。
• 奖励函数 $R$：表示在执行动作 $a$ 后，从状态 $s$ 转移到状态 $s^{\prime }$ 可能获得的奖励。
• 折扣因子 $\gamma$：用于衡量未来奖励的重要性，通常取值在 $0$ 到 $1$ 之间。

对于离散时间的马尔可夫决策过程，其动作空间和状态转移概率可以表示为：
$$P(s^{\prime },r|s,a)=\mathbb{P}(S_{t+1}=s^{\prime },R_{t+1}=r|S_t=s,A_t=a)$$

通过策略 $\pi (a|s)$，表示在状态 $s$ 下选择动作 $a$ 的概率，可以定义状态值函数 $V^{\pi }$ 和动作值函数 $Q^{\pi }$：
$$V^{\pi }(s)={\mathbb{E}}_{\pi }[G_t|S_t=s]$$$$Q^{\pi }(s,a)={\mathbb{E}}_{\pi }[G_t|S_t=s,A_t=a]$$
其中 $G_t$ 是折扣累积奖励：
$$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\dots$$

MDP的名词

1. 状态（State）： 表示系统或环境可能处于的各种情况或配置。状态集合 $S$ 。

2. 动作（Action）： 代理或决策者在某个状态下可以执行的操作。动作集合 $A$ 。

3. 状态转移矩阵（State Transition Matrix）：
   在马尔可夫决策过程（MDP）中，状态转移矩阵是一个描述状态之间转移概率的矩阵。如果有 $N$ 个状态，那么状态转移矩阵 $P$ 的元素 $P_{s,s^{\prime }}$ 表示在当前处于状态 $s$ 时，下一步转移到状态 $s^{\prime }$ 的概率。状态转移矩阵通常表示为：
   $$P=\left[\begin{array}{cccc}{P}_{1,1}& P_{1,2}& \dots & P_{1,N}\\ P_{2,1}& P_{2,2}& \dots & P_{2,N}\\ ⋮& ⋮& \ddots & ⋮\\ P_{N,1}& P_{N,2}& \dots & P_{N,N}\end{array}\right]$$

4. 状态转移概率（Transition Probability）： 表示在执行某个动作后，系统从一个状态转移到另一个状态的概率。通常用 $P(s^{\prime }|s,a)$ 表示在状态 $s$ 下执行动作 $a$ 后进入状态 $s^{\prime }$ 的概率。

5. 奖励函数（Reward Function）： 描述在执行某个动作后，从一个状态转移到另一个状态可能获得的即时奖励。通常用 $R(s,a,s^{\prime })$ 表示。

6. 折扣因子（Discount Factor）： 用符号 $\gamma$ 表示，用于衡量未来奖励的重要性。折扣因子在 $0$ 到 $1$ 之间，越接近 $1$ 表示越重视未来奖励。

7. 回报（Return）：
   在马尔可夫决策过程中，回报是决策者从起始状态开始，执行一系列动作并遵循某个策略后所获得的累积奖励。回报通常用 $G_t$ 表示，在时间步 $t$ 开始的回报定义为：
   $$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\dots =\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}$$
   其中，$R_{t+k+1}$ 是在时间步 $t+k+1$ 处获得的即时奖励，$\gamma$ 是折扣因子。

8. 策略（Policy）： 表示决策者在每个状态下选择动作的规则或方案。策略通常用符号 $\pi$ 表示，可以是确定性策略（确定每个状态下选择的动作）或随机策略（在每个状态下选择动作的概率分布）。

9. 价值函数（Value Function）： 衡量状态或状态-动作对的好坏程度，用于指导决策者的行为。有状态值函数 $V(s)$ 和动作值函数 $Q(s,a)$ 两种形式。

   • 状态值函数 $V(s)$： 表示在策略 $\pi$ 下从状态 $s$ 开始的预期折扣累积奖励。
   • 动作值函数 $Q(s,a)$： 表示在策略 $\pi$ 下从状态 $s$ 执行动作 $a$ 开始的预期折扣累积奖励。

10. 时间范围（Horizon）：
    时间范围指的是在一个马尔可夫决策过程中，代理或决策者考虑未来的时间步数。

动态规划

动态规划（DP）用于解决具有重叠子问题（在解一个问题时，需要多次解相同的子问题。动态规划通过保存已解决的子问题的结果，避免重复计算）和最优子结构（如果问题的最优解所包含的子问题的解也是最优的）的问题。它将一个问题分解为一系列相互重叠的子问题，并通过存储和重复计算已解决的子问题的结果来节省计算时间，从而实现高效求解整体问题。
因为马尔可夫决策过程（MDP）具有最优子结构和重叠子问题的性质。所以能够应用于强化学习中。

状态值函数和动作值函数

当谈论状态值函数和动作值函数时，通常指的是在强化学习中，用于度量不同状态或状态-动作对的价值的两个函数。这两个函数是对于某个特定策略（行为方式）而言的。

状态值函数：

状态值函数表示在某个状态下，特定策略下所能获得的期望累积回报。对于策略 $\pi$，状态 $s$ 的值函数表示为 $V^{\pi }(s)$。具体而言，$V^{\pi }(s)$ 是从状态 $s$ 开始，按照策略 $\pi$ 行动时所获得的期望回报。

$$V^{\pi }(s)={\mathbb{E}}_{\pi }\left[G_t\mid S_t=s\right]$$

其中，$G_t$ 是从时刻 $t$ 开始的累积回报，${\mathbb{E}}_{\pi }$ 表示在策略 $\pi$ 下的期望。

动作值函数：

动作值函数表示在某个状态下，采取某个特定动作后，按照特定策略所能获得的期望累积回报。对于策略 $\pi$，状态 $s$ 中采取动作 $a$ 的值函数表示为 $Q^{\pi }(s,a)$。具体而言，$Q^{\pi }(s,a)$ 是在状态 $s$ 采取动作 $a$，然后按照策略 $\pi$ 行动时所获得的期望回报。

$$Q^{\pi }(s,a)={\mathbb{E}}_{\pi }\left[G_t\mid S_t=s,A_t=a\right]$$

其中，$G_t$ 是从时刻 $t$ 开始的累积回报，${\mathbb{E}}_{\pi }$ 表示在策略 $\pi$ 下的期望。

两者关系

1. 状态值函数 $V^{\pi }(s)$ 和动作值函数 $Q^{\pi }(s,a)$ 之间的关系：
   $$V^{\pi }(s)=\sum _a\pi (a|s)Q^{\pi }(s,a)$$

   这个关系表达了在策略 $\pi$ 下，当前状态 $s$ 的值等于在当前状态下对所有可能动作 $a$ 采取的动作值函数 $Q^{\pi }(s,a)$ 的加权和，其中权重是按照策略 $\pi$ 选择动作 $a$ 的概率。

2. 动作值函数 $Q^{\pi }(s,a)$ 和状态值函数 $V^{\pi }(s)$ 之间的关系：
   $$Q^{\pi }(s,a)={\mathbb{E}}_{\pi }\left[R_{t+1}+\gamma V^{\pi }(S_{t+1})\mid S_t=s,A_t=a\right]$$

   这个关系表达了在策略 $\pi$ 下，当前状态 $s$ 采取动作 $a$ 的动作值函数等于在执行动作 $a$ 后，根据策略 $\pi$ 转移到下一状态 $S_{t+1}$ 并获得奖励 $R_{t+1}$ 的期望值加上未来折现的状态值函数 $V^{\pi }(S_{t+1})$。

• 状态值函数 $V^{\pi }(s)$ 衡量的是在某个状态下策略的期望回报。
• 动作值函数 $Q^{\pi }(s,a)$ 衡量的是在某个状态下采取某个动作后的期望回报。

状态&动作值函数的贝尔曼方程

推导：状态值函数➡贝尔曼方程

通过考虑状态值函数与下一个状态值函数之间的关系来推导。使用贝尔曼方程可以表示状态值函数之间的递归关系，具体形式如下：

$$V^{\pi }(s)={\mathbb{E}}_{\pi }\left[G_t\mid S_t=s\right]$$

其中，$G_t$ 是从时刻 $t$ 开始的累积回报，${\mathbb{E}}_{\pi }$ 表示在策略 $\pi$ 下的期望。

贝尔曼方程将状态值函数与下一时刻的状态值函数联系起来。具体可以将 $G_t$ 展开为当前奖励 $R_{t+1}$ 加上未来的累积回报：

$$V^{\pi }(s)={\mathbb{E}}_{\pi }\left[R_{t+1}+\gamma G_{t+1}\mid S_t=s\right]$$

其中，$\gamma$ 是折扣因子，控制对未来回报的重视程度。
将 $G_{t+1}$ 进一步展开为下一个时刻的状态值函数：
$$V^{\pi }(s)={\mathbb{E}}_{\pi }\left[R_{t+1}+\gamma V^{\pi }(S_{t+1})\mid S_t=s\right]$$
这就是状态值函数的贝尔曼方程。它表示在策略 $\pi$ 下，当前状态 $s$ 的值等于当前时刻获得的奖励 $R_{t+1}$ 加上折扣因子乘以下一状态 $S_{t+1}$ 的值的期望。

贝尔曼方程

马尔可夫决策过程（MDP）具有最优子结构和重叠子问题的性质，这是因为MDP的值函数满足贝尔曼方程（动态规划方程），这一方程本身就包含了最优子结构和重叠子问题的特性。

状态值函数的贝尔曼方程

对于状态值函数 $V^{\pi }(s)$ 来说，贝尔曼方程的形式如下：

$$V^{\pi }(s)=\sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)\left[r+\gamma V^{\pi }(s^{\prime })\right]$$

这个方程表示，在策略 $\pi$ 下，当前状态 $s$ 的值等于当前状态下采取所有可能动作 $a$ 的值的期望。具体来说：

• $V^{\pi }(s)$：在策略 $\pi$ 下，从状态 $s$ 开始的累积回报的期望值。

• ${\sum }_a\pi (a|s)$：对所有可能的动作 $a$ 求和，按照策略 $\pi$ 选择动作 $a$ 的概率。

• ${\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)$：对所有可能的下一状态 $s^{\prime }$ 和奖励 $r$ 求和，表示在当前状态 $s$ 采取动作 $a$ 后，转移到下一状态 $s^{\prime }$ 且得到奖励 $r$ 的概率。

• $\left[r+\gamma V^{\pi }(s^{\prime })\right]$：在当前状态 $s$ 采取动作 $a$ 后，得到奖励 $r$ 并按照策略 $\pi$ 转移到下一状态 $s^{\prime }$ 的累积回报。这个值乘以 $\gamma$ 表示对未来回报的折现。

动作值函数的贝尔曼方程：

对于动作值函数 $Q^{\pi }(s,a)$ 来说，贝尔曼方程的形式如下：

$$Q^{\pi }(s,a)=\sum _{s^{\prime },r}p(s^{\prime },r|s,a)\left[r+\gamma \sum _{a^{\prime }}\pi (a^{\prime }|s^{\prime })Q^{\pi }(s^{\prime },a^{\prime })\right]$$

这个方程表示，在策略 $\pi$ 下，当前状态 $s$ 采取动作 $a$ 的值等于在转移到下一状态 $s^{\prime }$ 且得到奖励 $r$ 的概率为 $p(s^{\prime }|s,a)$ 时，累积回报的期望值。具体来说：

• $Q^{\pi }(s,a)$：在策略 $\pi$ 下，从状态 $s$ 开始，在采取动作 $a$ 后的累积回报的期望值。

• ${\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)$：对所有可能的下一状态 $s^{\prime }$ 和奖励 $r$ 求和，表示在当前状态 $s$ 采取动作 $a$ 后，转移到下一状态 $s^{\prime }$ 且得到奖励 $r$ 的概率。

• $\left[r+\gamma {\sum }_{a^{\prime }}\pi (a^{\prime }|s^{\prime })Q^{\pi }(s^{\prime },a^{\prime })\right]$：在当前状态 $s$ 采取动作 $a$ 后，得到奖励 $r$ 并按照策略 $\pi$ 转移到下一状态 $s^{\prime }$ 的累积回报。这个值乘以 $\gamma$ 表示对未来回报的折现。

---

在强化学习中，动态规划（Dynamic Programming）是一种基于状态值函数或动作值函数的迭代方法，用于求解马尔可夫决策过程（MDP）中的最优策略。动态规划方法分为两类：策略评估和策略改进。

动态规划方法

1. 策略评估（Policy Evaluation）：

策略评估的目标是计算给定策略下的状态值函数或动作值函数。它通过迭代计算值函数，直到收敛为止。这一过程使用贝尔曼方程（Bellman Equation）来更新值函数。

• 状态值函数$V^{\pi }$的更新：
  $$V^{\pi }(s)\leftarrow \sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma V^{\pi }(s^{\prime })]$$

• 动作值函数$Q^{\pi }$ 的更新：
  $$Q^{\pi }(s,a)\leftarrow \sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma \sum _{a^{\prime }}\pi (a^{\prime }|s^{\prime })Q^{\pi }(s^{\prime },a^{\prime })]$$

这个过程会持续进行迭代，直到值函数收敛到真实值函数。

2. 策略改进（Policy Improvement）：

策略改进的目标是在已经计算得到的值函数的基础上，进一步改进策略。这一过程基于贪婪策略（Greedy Policy）选择能够最大化值函数的动作。

• 贪婪策略 ${\pi }^{\prime }(s)={\text{argmax}}_a{Q}^{\pi }(s,a)$

策略改进将当前的策略更新为更优的策略，然后进行下一轮的策略评估和策略改进，迭代进行直到策略不再改变为止。最终，该过程得到了最优策略和相应的值函数。

迭代

策略迭代（Policy Iteration）： 策略迭代是一种结合策略评估和策略改进的方法，通过反复进行策略评估和策略改进的迭代，最终得到最优策略。

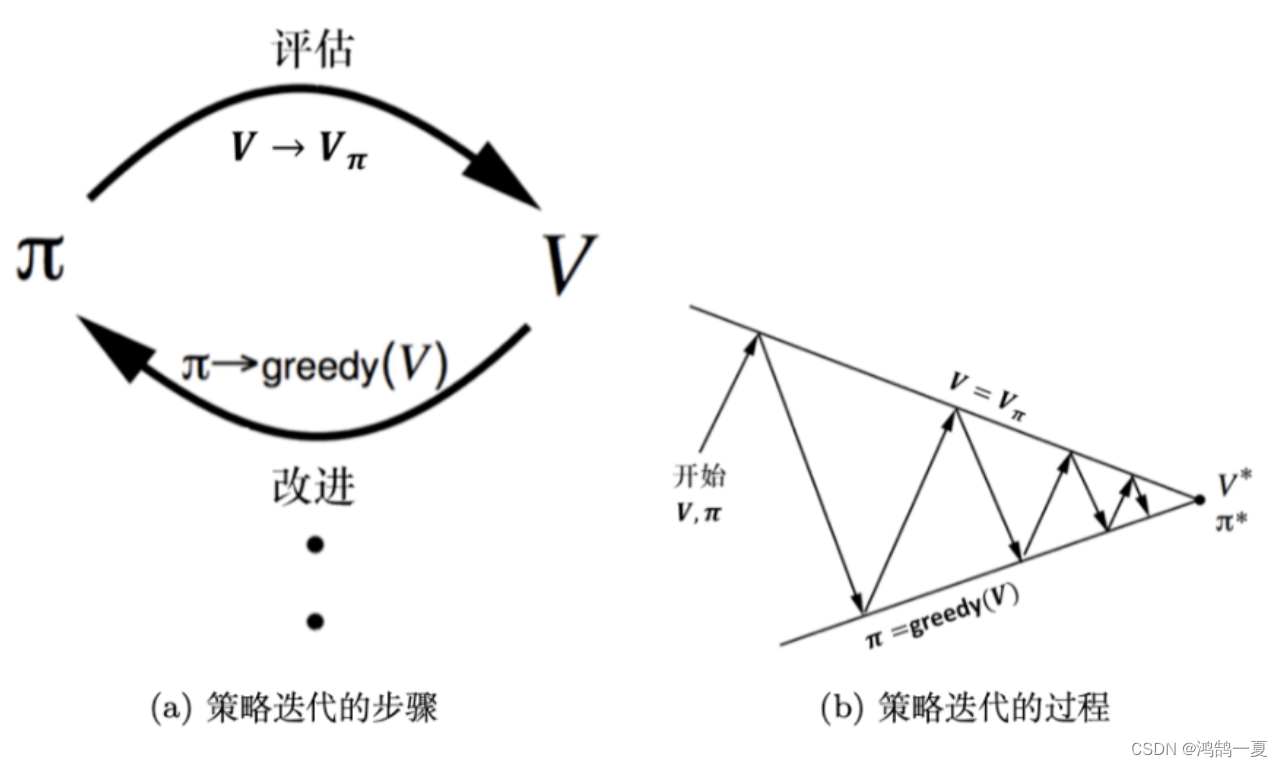
值迭代（Value Iteration）： 值迭代是一种单步同时更新所有状态的值函数的方法，通过迭代计算值函数，最终得到最优值函数，从而得到最优策略。

对比策略迭代和值迭代

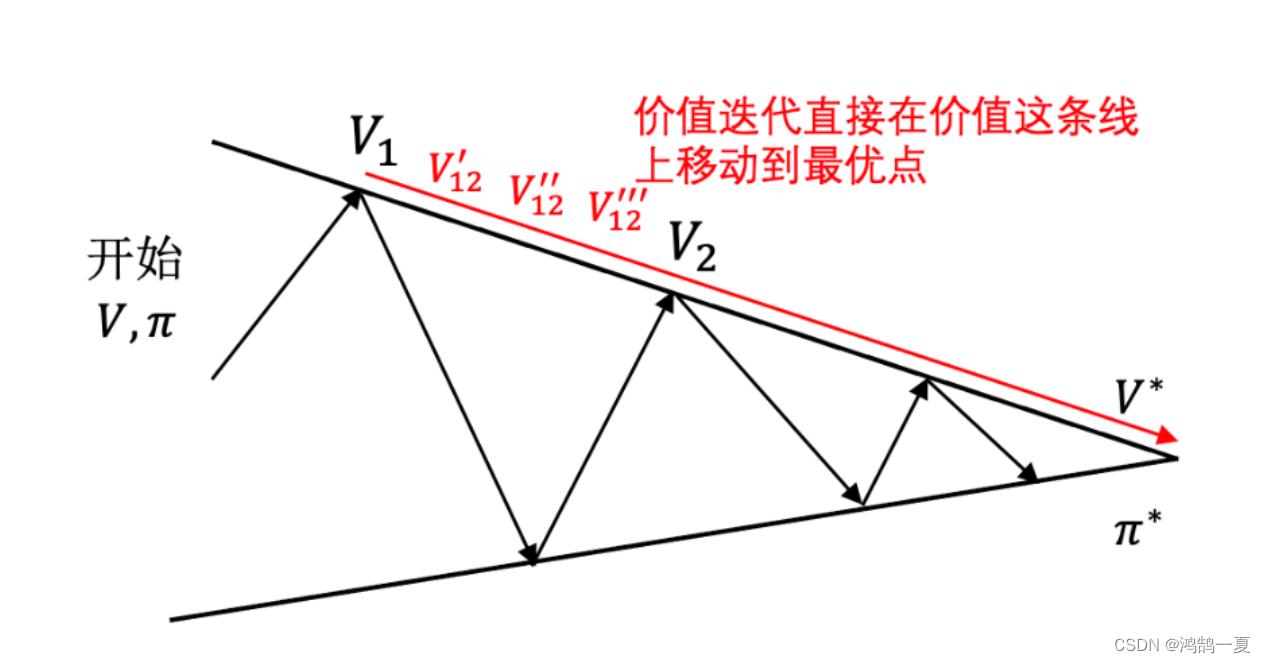
总结：

1. 策略评估（Policy Evaluation）：

   • 目标： 计算给定策略下的状态值函数（$V^{\pi }$）或动作值函数（$Q^{\pi }$）。
   • 方法： 通过迭代或解线性方程组等方式，更新值函数，直到收敛为止。

2. 策略改进（Policy Improvement）：

   • 目标： 在已经计算得到的值函数的基础上，进一步改进策略。
   • 方法： 贪婪地选择能够最大化值函数的动作，形成新的策略。

3. 策略迭代（Policy Iteration）：

   • 方法： 交替进行策略评估和策略改进，直到策略不再改变。策略迭代保证最终收敛到最优策略和最优值函数。
   • 步骤：
     1. 初始策略 ${\pi }_0$.
     2. 迭代进行策略评估，计算 $V^{{\pi }_i}$.
     3. 迭代进行策略改进，得到新的策略 ${\pi }_{i+1}$.
     4. 重复步骤2和步骤3，直到策略不再改变。

4. 值迭代（Value Iteration）：

   • 目标： 直接计算最优值函数（$V^{\ast }$或$Q^{\ast }$）。
   • 方法： 通过迭代更新值函数，直到收敛。值迭代的每一步都是通过贝尔曼最优方程进行更新。
   • 步骤：
     1. 初始化值函数 $V_0$.
     2. 迭代进行值函数更新，计算 $V_{i+1}$.
     3. 重复步骤2，直到 $V_i$ 收敛。