动态规划思想——最优二叉搜索树问题（附完整的代码）

问题：

最优二叉搜索树问题的问题提出是，设S={x1, x2, ..., xn}是一个由n个关键字组成的线性有序集，(a0, b1, a1, ..., bn, an) 为集合S的存取概率分布，表示有序集S的二叉搜索树利用二叉树的节点存储有序集中的元素。在二叉搜索树中搜索一个元素x。在二叉搜索树的内部结点中找到x的概率为bj；在二叉搜索树的叶结点中确定x的概率为ai。最优二叉搜索树问题要求找出搜索成本最低的二叉搜索树。设n=3，b(1:3)={0.5,0.1,0.05}，a(1:4)={0.15,0.1,0.05,0.05}。

 

需求：采用动态规划算法求该最优二叉搜索树，将算法编程实现

❤ (ɔˆз(ˆ⌣ˆc)“玥”——乃古上神珠也。见者好运连连，点个关注，咱们来玥方长！

(ง •̀_•́)ง加油😁😁😁

目录

❤ (ɔˆз(ˆ⌣ˆc)“玥”——乃古上神珠也。见者好运连连，点个关注，咱们来玥方长！

一、概念

二、问题描述

三、实现算法代码

四、运行结果

 总结

---

 

一、概念

• 二叉搜索树：在二叉树中，对任意的节点X其左子树的所有节点都不大于X.key，其右子树的所有节点都不小于X.key。满足此条件的二叉树称为二叉搜索树。对二叉搜索树进行中序遍历将会得到一个单调递增的数列。
• 最优二叉树：在二叉树中，不同的节点都有不同的访问频率。为了减少查找某个节点所需要遍历的次数，通过将访问频率最高的节点放在离根节点近的位置，这样就可以减少平均遍历次数。最优二叉树又称赫夫曼树。
• 最优二叉搜索树：就是满足二叉搜索树性质的最优二叉树。

二、问题描述

现在给定一组有序节点的查找概率，以及查找失败的概率。关键字k1,k2,k3,...,kn的查找的概率分别为p1,p2,p3,...,pn. 对于查找失败的伪关键字，有n+1个分别为：d0,d1,d2,d3,...,dn. 其分别对于的查找概率为：q0,q1,q2,...,qn。假设现在有五个节点，每个节点的概率为p1,p2,...,p5。qi表示伪关键字di的概率，分别为q0,q1,q2,...,q5。如下表：

声明： 本部分内容转载自：动态规划之最优二叉搜索树（算法导论） - 走看看

 

三、实现算法代码

class BinarySearchTree
{
    /**
     * 仅供参考，学习所用
     * author:来玥方长
     * time:2022-5-23
     * @param a  叶子结点
     * @param b  内部结点
     * @param m  搜索成本
     * @param w  存取概论
     */
    public static void optimalBinarySearchTree(double []a,double []b,
    double [][]m,int [][]s,double [][]w)
    {
        int n=b.length-1;
        for(int i=0;i<=n;i++) //初始化
        {
            w[i+1][i]=a[i];
            m[i+1][i]=0;
        }
        for(int r=0;r<n;r++) //r=0,1,2分别对应有r个内部结点的最优二叉树
        {
            for(int i=1;i<=n-r;i++)
            {
                int j=i+r;
                w[i][j]=w[i][j-1]+a[j]+b[j];
                m[i][j]=m[i][i-1]+m[i+1][j];
                s[i][j]=i;
                for(int k=i+1;k<=j;k++)
                {
                    double t=m[i][k-1]+m[k+1][j];
                    if(t<m[i][j])
                    {
                        m[i][j]=t;
                        s[i][j]=k;
                    }
                }
                m[i][j] +=w[i][j];
            }
        }
        /**
         * 输出结果
         */
        System.out.println("m[i][j]=");
        for(int i=1;i<=n+1;i++){
            for(int j=0;j<=n;j++){
                System.out.print(m[i][j]+"\t");}
            System.out.println();
        }
        System.out.println("w[i][[j]=");
        for(int i=1;i<=n+1;i++){
            for(int j=0;j<=n;j++){
                System.out.print(w[i][j]+"\t");}
            System.out.println();
        }
        System.out.println("s[i][j]=");
        for(int i=1;i<=n+1;i++){
            for(int j=0;j<=n;j++){
                System.out.print(s[i][j]+"\t");}
            System.out.println();
        }
        System.out.println("所构造的最优二叉搜索树最低的搜索成本为"+m[1][n]);
    }

    public static void main(String[]args)
    {
        double b[] = {0,0.5,0.1,0.05};  //内部结点
	    double a[] = {0.15,0.1,0.05,0.05}; //叶子结点
        int n=a.length+2;
        double m[][]=new double[n][n];
        int s[][]=new int[n][n];
        double w[][]=new double[n][n];
        optimalBinarySearchTree(a, b, m, s, w);
    }
}

 

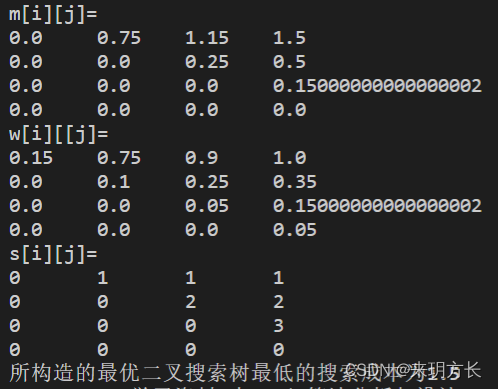
四、运行结果

 

 

 总结

路漫漫其修远兮，吾将上下而求索！！！