AcWing 数学知识

质数

模板：

// 试除法判断质数
bool is_prime(int x)
{
    if (x < 2) return false;
    //只需枚举一部分 使得 i<= x / i, 时间复杂度为√n
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
            return false;
    return true;
}

// 试除法分解质因数
void divide(int n)
{
    for (int i = 2; i <= n / i; i++)
    {
        if (n % i == 0)
        {
            int cnt = 0;
            while (n % i == 0)
            {
                n /= i;
                cnt++;
            }
            printf("%d %d\n", i, cnt);
        }
    }
    
    //本身就是质数
    if (n > 1) printf("%d %d\n", n, 1);
    printf("\n");
}

// 

试除法判定质数

代码：

#include<iostream>
using namespace std;
int n;

bool is_prime(int x)
{
    if (x == 1) return false;
    for (int i = 2; i <= x / i; i++)
    {
        if (x % i == 0) return false;
    }
    
    return true;
}

int main()
{
    scanf("%d", &n);
    while (n--)
    {
        int a;
        scanf("%d", &a);
        printf(is_prime(a) ? "Yes\n" : "No\n");
    }
    return 0;
}

分解质因数

代码：

#include<iostream>
using namespace std;

void divide(int n)
{
    for (int i = 2; i <= n / i; i++)
    {
        if (n % i == 0)
        {
            int cnt = 0;
            while (n % i == 0)
            {
                n /= i;
                cnt++;
            }
            printf("%d %d\n", i, cnt);
        }
    }
    
    //本身就是质数
    if (n > 1) printf("%d %d\n", n, 1);
    printf("\n");
}

int main()
{
    int n;
    scanf("%d", &n);
    
    while (n--)
    {
        int a;
        scanf("%d", &a);
        divide(a);
    }
    
    return 0;
}

筛质数

思路：
筛法求质数，有两种方式：

• 埃氏筛法
• 线性筛法

埃氏筛法
埃氏筛法每次筛掉质数的倍数（大于等于2倍），这样最后剩下的就全是质数。$st[i]$为$false$时，表示为质数。

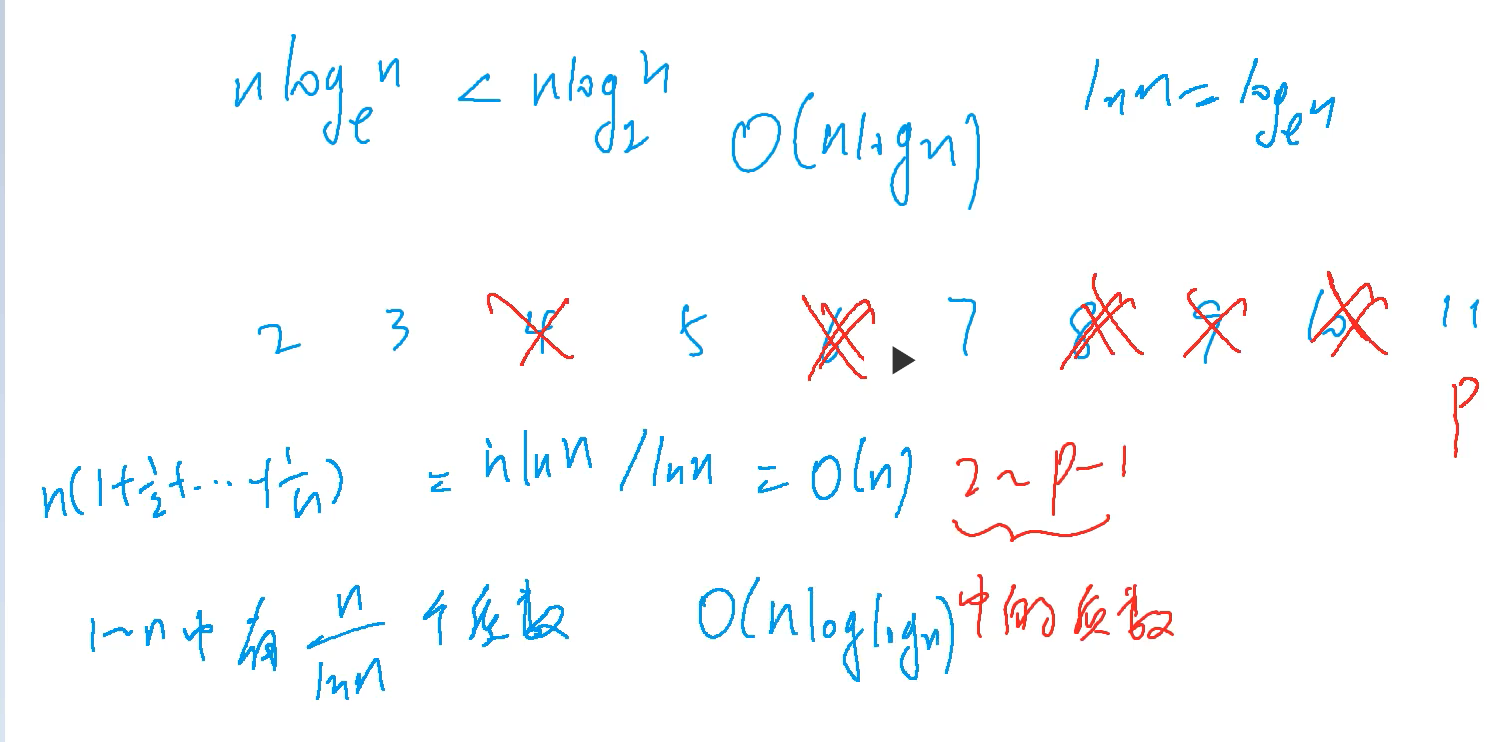
埃氏筛法代码：

#include<iostream>
using namespace std;

const int N = 1000010;
bool st[N];
int primes[N];
int cnt;

void get_primes(int n)
{
    for (int i = 2; i <= n; i++)
    {
        if (!st[i]) primes[cnt++] = i;
        for (int j = i + i; j <= n; j += i) st[j] = true;
    }
}

int main()
{
    int n;
    cin >> n;
    get_primes(n);
    cout << cnt << endl;
    
    return 0;
}

线性筛法
线性筛法保证$n$只会被最小质因子筛掉。

• i % primes[j] == 0，primes[j]是i的最小质因子，primes[j]是primes[j] * i的最小质因子。
• i % primes[j] != 0，primes[j]小于i的最小质因子，primes[j]是primes[j] * i的最小质因子。

bool st[N];
int primes[N];
int cnt;

void get_primes(int n)
{
    for (int i = 2; i <= n; i++)
    {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] <= n / i; j ++) 
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
            
    }
}

线性筛法代码：

#include<iostream>
using namespace std;

const int N = 1000010;
bool st[N];
int primes[N];
int cnt;

void get_primes(int n)
{
    for (int i = 2; i <= n; i++)
    {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] <= n / i; j ++) 
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
            
    }
}

int main()
{
    int n;
    cin >> n;
    get_primes(n);
    cout << cnt << endl;
    
    return 0;
}

约数

试除法求约数

代码：

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int n;

void get_divisors(int a)
{
    vector<int> res;
    for (int i = 1; i <= a / i; i++)
    {
        if (a % i == 0)
        {
            res.push_back(i);
            // 防止平方根多次出现
            if (i != a / i) res.push_back(a / i);
        }
    }
    
    //从大到小排序
    sort(res.begin(), res.end());
    
    for (int t : res) printf("%d ", t);
    printf("\n");
    
}

int main()
{
    scanf("%d", &n);
    while (n--)
    {
        int a;
        scanf("%d", &a);
        get_divisors(a);
    }
    return 0;
}

约数个数

思路：
给定一个数$N$，$p_i$为$N$的质约数，则可以表示为:
$$N=p_1^{{\alpha }_1}\times p_2^{{\alpha }_2}\times p_3^{{\alpha }_3}\times ...\times p_k^{{\alpha }_k}$$
$N$的每一个约数$d_i$，可以表示为:
$$d_i=p_1^{{\beta }_1}\times p_2^{{\beta }_2}\times p_3^{{\beta }_3}\times ...\times p_k^{{\beta }_k}$$
其中，$0\le {\beta }_i\le {\alpha }_i$， ${\beta }_i$的选法有$0\sim {\alpha }_i$，共有$({\alpha }_i+1)$种选法 ，根据排列组合原理，约数个数为：
$$({\alpha }_1+1)\times ({\alpha }_2+1)\times ({\alpha }_3+1)\times ...\times ({\alpha }_k+1)$$

依次遍历$a_i$，求$a_i$的质因数以及每个质因数的个数，可以用哈希表保存结果

代码：

#include<iostream>
#include<unordered_map>
using namespace std;

const int mod = 1e9 + 7;


int main()
{
    int n;
    cin >> n;
    unordered_map<int, int> primes;
    while (n--)
    {
        int x;
        cin >> x;
        for (int i = 2; i <= x / i; i++)
        {
            while (x % i == 0)
            {
                x /= i;
                primes[i]++;
            }
        }
        if (x > 1) primes[x]++;
    }
    
    long long res = 1;
    
    for (auto prime : primes) 
    	res = res * (prime.second + 1) % mod;
    
    cout << res << endl;
    
    return 0;
}

约数之和

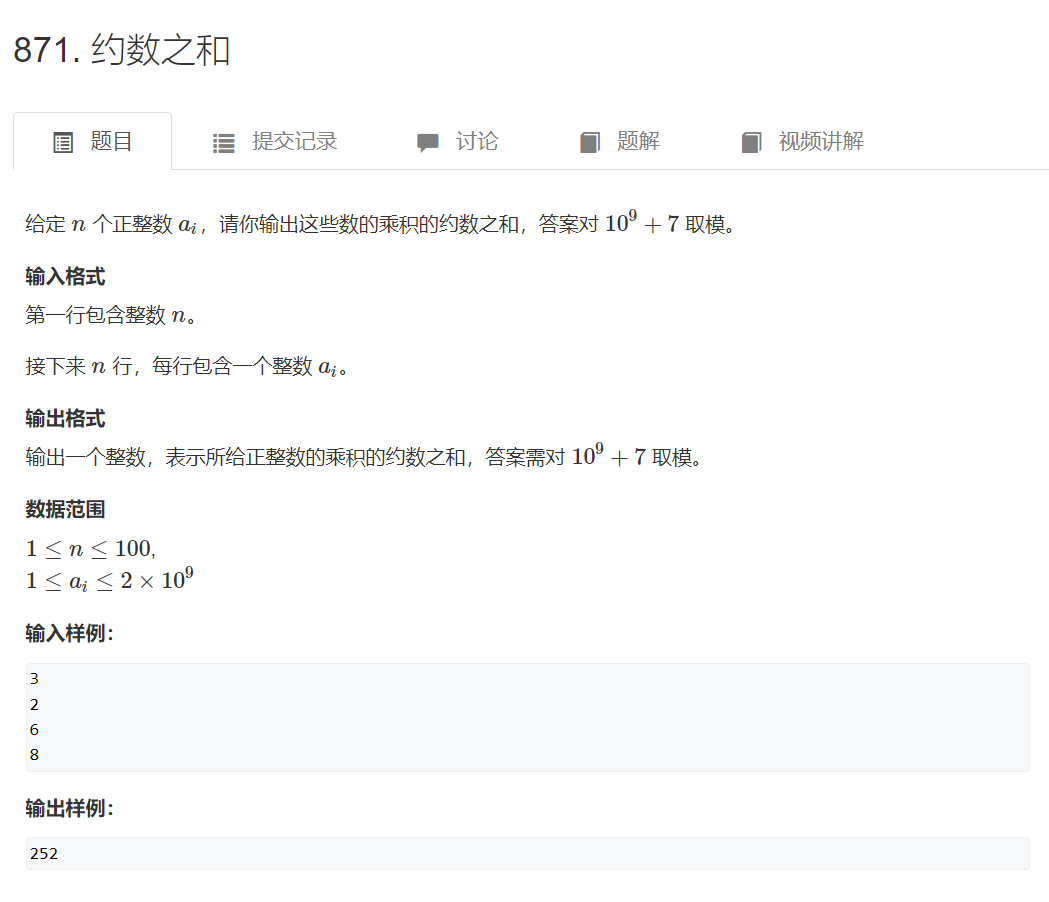
思路：
根据约数个数的思路，约数之和为$$d_1+d_2+d_3+...+d_k①$$
其中， $$d_i=p_1^{{\beta }_1}\times p_2^{{\beta }_2}\times p_3^{{\beta }_3}\times ...\times p_k^{{\beta }_k}②$$
约数之和为$$(p_1^0+p_1^1+p_1^2...+p_1^{{\alpha }_1})...(p_k^0+p_k^1+p_k^2...+p_k^{{\alpha }_k})$$
展开可得式①，展开的每一项均为$d_i$

$(p_i^0+p_i^1+p_i^2...+p_i^{{\alpha }_1})$可以按照下面的方式进行推导：
$t_0=1$
$t_1=t_0\times p+1=p+1$
$t_2=t_1\times p+1=p^2+p+1$
…
$t_{{\alpha }_i}=t_{{\alpha }_i-1}\times p+1=p^{{\alpha }_i}+p^{{\alpha }_i-1}+...+p+1$，
最后计算$\prod _{i=1}^n{t}_{{\alpha }_i}$，即为约数之和。

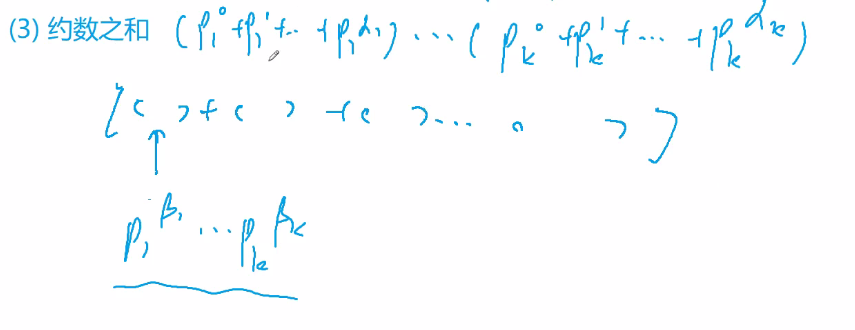
代码：

#include<iostream>
#include<unordered_map>
using namespace std;

const int mod = 1e9 + 7;


int main()
{
    int n;
    cin >> n;
    unordered_map<int, int> primes;
    while (n--)
    {
        int x;
        cin >> x;
        for (int i = 2; i <= x / i; i++)
        {
            while (x % i == 0)
            {
                x /= i;
                primes[i]++;
            }
        }
        if (x > 1) primes[x]++;
    }
    
    long long res = 1;
    
    for (auto prime : primes) 
    {
        long long t = 1;
        int p = prime.first, a = prime.second;
        while (a--) t = (t * p + 1) % mod;
        res = res * t % mod;
    }
    
    cout << res << endl;
    
    return 0;
}

最大公因数

思路：
欧几里得算法，辗转相除法。
代码：

#include<iostream>
using namespace std;

int gcd(int m, int n)
{
    return m % n == 0 ? n : gcd(n, m % n);
}

int main()
{
    int n;
    cin >> n;
    while (n--)
    {
        int a, b;
        cin >> a >> b;
        cout << gcd(a, b) << endl;
    }
    return 0;
}

欧拉函数

欧拉函数

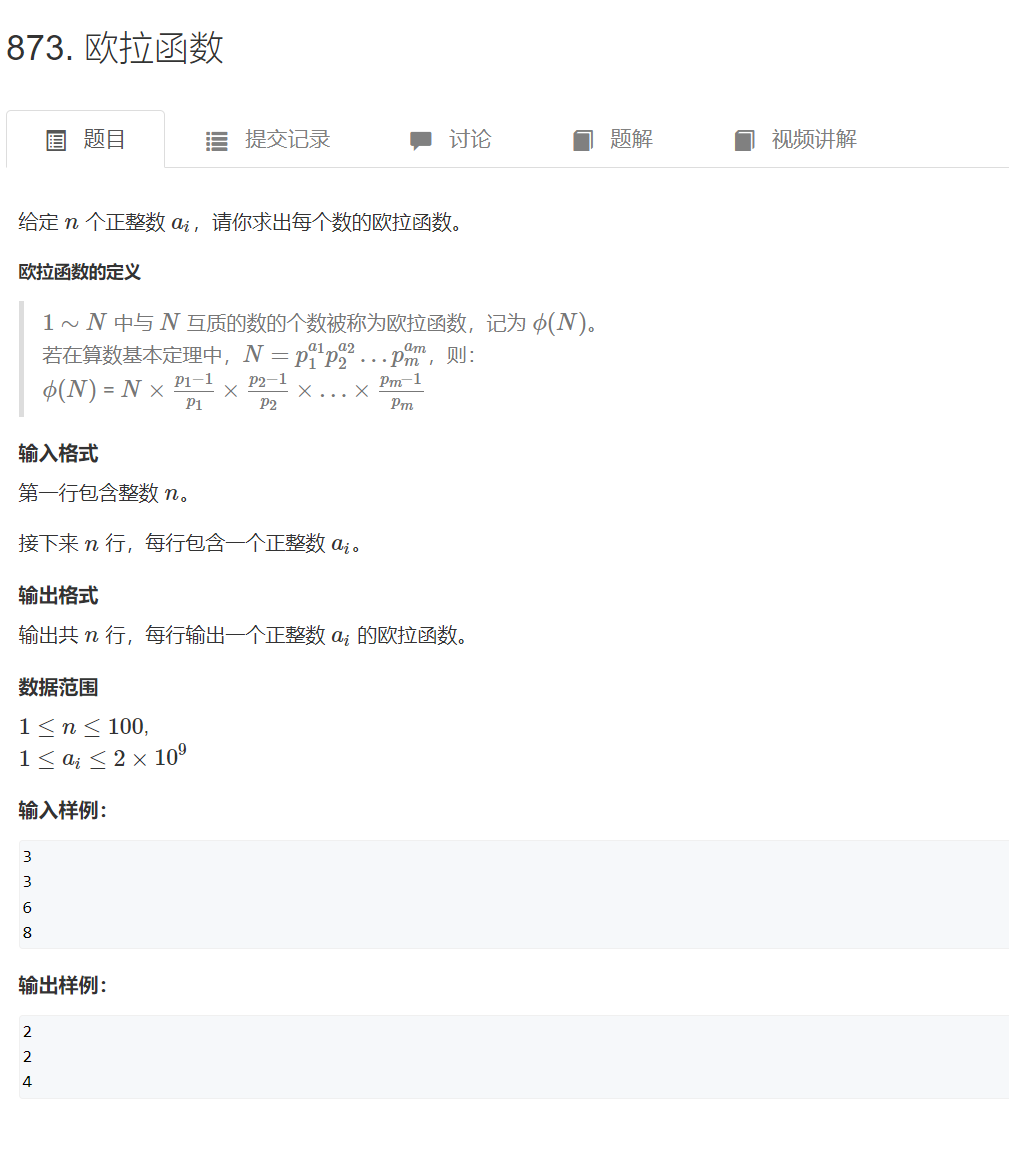
思路：
互质是公约数只有1的两个整数。在算数基本定理中，$N=p_1^{{\alpha }_1}\times p_2^{{\alpha }_2}\times p_3^{{\alpha }_3}\times ...\times p_m^{{\alpha }_m}$，根据欧拉函数的定义：$$\varphi (N)=N\times \frac{p_1-1}{p_1}\times \frac{p_2-1}{p_2}\times ...\times \frac{p_m-1}{p_m}$$
只需求得$N$的质因数$p_i$即可，可以用到分解质因数的方法。
代码：

#include<iostream>
using namespace std;


int main()
{
    int n;
    cin >> n;
    while (n--)
    {
        int x;
        cin >> x;
        int res = x;
        for (int i = 2; i <= x / i; i++)
        {
        	// 分解质因数
            if (x % i == 0)
            {
                res = res / i * (i - 1);
                while (x % i == 0) x /= i;
            }
        }
        // 最后的质因数
        if (x > 1) res = res / x * (x - 1);
        
        cout << res << endl;
    }
    return 0;
}

筛法求欧拉函数

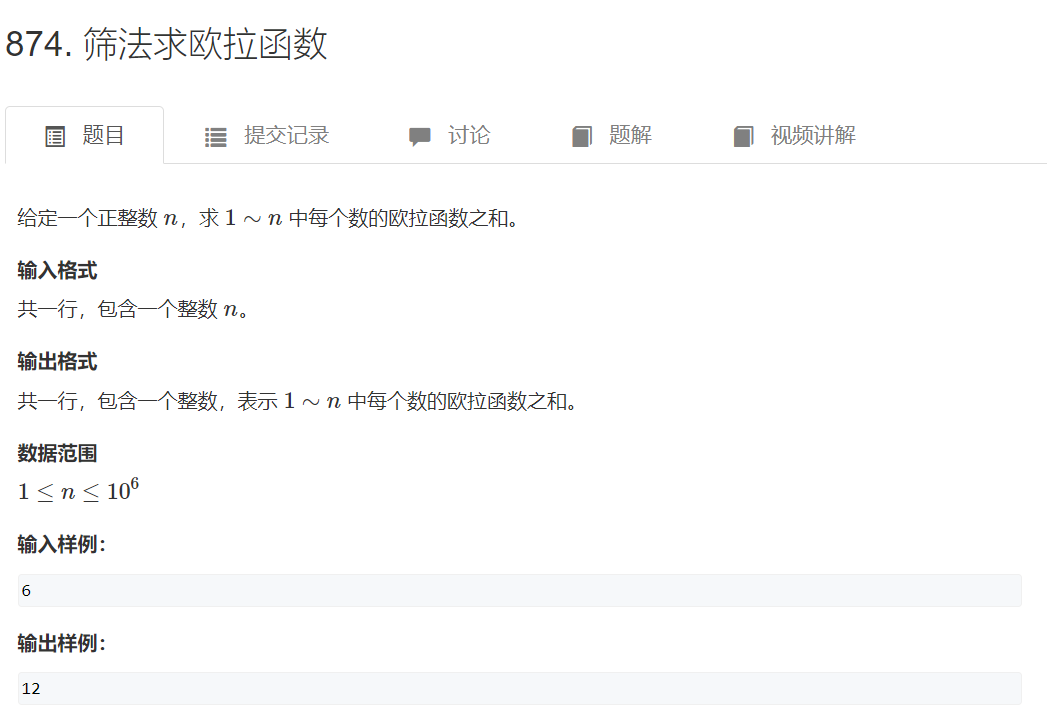
思路：
在用线性筛法求质因数的过程中，可以同时求出很多东西，比如某个数的欧拉函数。$1\sim N$中与$N$互质的数的个数即为$N$的欧拉函数，记作$\varphi (N)$。

• 若$N$为质数，则$\varphi (N)=N-1$
• 若$N$不为质数，$N$只会被最小的质因数给筛掉。
  记$p_j$为$N$的质因子，枚举$2\sim N$，记作$i$。
  • 若 $i\mathrm{mod}{p}_j=0$，则$p_j$为$p_j\times i$的最小质因子，根据欧拉函数的计算公式:$$\varphi (p_j\times i)=(p_j\times i)\times \frac{p_1-1}{p_1}\times \frac{p_2-1}{p_2}\times ...\times \frac{p_k-1}{p_k}$$ $p_1\sim p_k$均为 $i$的质因子， p j ∈ { p 1 , . . . , p k } p_j \in \{p_1,...,p_k\} pj​∈{p1​,...,pk​}。
    观察$i\times \frac{p_1-1}{p_1}\times \frac{p_2-1}{p_2}\times ...\times \frac{p_k-1}{p_k}$，可以用$\varphi (i)$表示，则$\varphi (p_j\times i)=p_j\times \varphi (i)$
  • $i\mathrm{mod}{p}_j\ne 0$，$p_j$小于$i$的最小质因子，则$p_j$是$p_j\times i$的最小质因子
    $$\begin{array}{rl}\varphi (p_j\times i)& =(p_j\times i)\times \frac{p_1-1}{p_1}\times ...\times \frac{p_j-1}{p_j}\times ...\times \frac{p_k-1}{p_k}\\ & =(i\times \frac{p_1-1}{p_1}\times \frac{p_2-1}{p_2}\times ...\times \frac{p_k-1}{p_k})\times (p_j\times \frac{p_j-1}{p_j})\\ & =\varphi (i)\times (p_j-1)\end{array}$$
    这样，便能遍历一次，求出$1\sim N$内所有欧拉函数之和，这就是筛法求欧拉函数。

欧拉定理，若$a$与$n$互质，则$a^{\varphi (n)}\equiv 1(modn)$
证明：
$1\sim n$中与$n$互质的数为
$$a_1,a_2,a_3...,a_{\varphi (n)}$$
每个数$\times a$，得
$$a{a}_1,a{a}_2,a{a}_3,...,a{a}_{\varphi (n)}$$
每个数都与$n$互质，在模$n$的概念下，两组数可看作相同的，则有下式：
$$\begin{array}{rl}{a}_1{a}_2{a}_3...a_{\varphi (n)}& \equiv a{a}_{1}a{a}_{2}a{a}_3...a{a}_{\varphi (n)}(modn)\\ a^{\varphi (n)}& \equiv 1(modn)\end{array}$$

特例： 费马定理
若$p$为质数，则$a^{\varphi (p)}\equiv 1(modp)$，即$a^{p-1}\equiv 1(modp)$

代码：

#include<iostream>
using namespace std;

typedef long long ll;

const int N = 1000010;
int primes[N], phi[N], cnt;
bool st[N];

ll get_eulers(int n)
{
    ll res = 0;
    phi[1] = 1;
    
    for (int i = 2; i <= n; i++)
    {
        if (!st[i]) primes[cnt++] = i, phi[i] = i - 1;
        for (int j = 0; primes[j] <= n / i; j++)
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0)
            {
                phi[primes[j] * i] = phi[i] * primes[j];
                break;
            }
            phi[primes[j] * i] = phi[i] * (primes[j] - 1);
        }
    }
    
    for (int i = 1; i <= n; i++) res += phi[i];
    
    return res;
}

int main()
{
    int n;
    cin >> n;
    cout << get_eulers(n) << endl;
    return 0;
}

快速幂

快速幂

思路：
快速幂的思想是将指数$k$看作二进制数之和这样便可以在$O(logk)$的复杂度中求得结果。则推出下式
$$\begin{array}{rl}k& =2^i+...+2^j+...+2^{\log k}\\ a^k& =a^{2^i}...a^{2^j}...a^{2^{\log k}}\end{array}$$
又知
$$\begin{array}{rl}{a}^{2^0}& =a\\ a^{2^1}& =a^{2^0\times 2}=(a^{2^0}{)}^2\\ ...& \\ a^{2^{\log k}}& =a^{2^{(\log k)-1}\times 2}=(a^{2^{(\log k)-1}}{)}^2\end{array}$$
若$k$第$i$位为$1$，则结果$\times a^{2^i}modp$，同时$k$右移一位，底数平方得$a^{2^{i+1}}$ ，$modp$，继续计算下一位。
代码

#include<iostream>
using namespace std;

typedef long long ll;

int q_pow(int a, int b, int p)
{
    int res = 1 % p;
    while (b)
    {
        if (b & 1) res = (ll) res * a % p;
        b >>= 1;
        a = (ll) a * a % p;
    }
    return res;
}

int main()
{
    int n;
    scanf("%d", &n);
    
    while (n--)
    {
        int a, b, p;
        scanf("%d%d%d", &a, &b, &p);
        printf("%d\n", q_pow(a, b, p));
    }
    
    return 0;
}

快速幂求逆元

思路：
若整数$b$ ，$m$ 互质，并且对于任意的整数 $a$，如果满足 $b|a$，则存在一个整数 $x$，使得 $a/b\equiv a\times x(modm)$，则称$x$ 为 $b$ 的模 $m$ 乘法逆元，记为 $b^{-1}(modm)$。
$$\begin{array}{rl}a/b& \equiv a\times x(modm)\\ a/b\times b& \equiv a\times b\times x(modm)\\ b\times x& \equiv 1(modm)\end{array}$$
又根据费马定理，$b^{m-1}\equiv 1(modm)$，则$b\times x=b^{m-1}$，$x=b^{m-2}$，若整数$b$ ，$m$ 互质，则存在$b$的乘法逆元。

代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
int n;

int qmi(int a, int b, int p)
{
    int res = 1 % p;
    while (b)
    {
        if (b & 1) res = (LL) res * a % p;
        b >>= 1;
        a = (LL) a * a % p;
    }
    return res;
}

int main()
{
    scanf("%d", &n);
    int a, p;
    while (n -- )
    {
        scanf("%d%d", &a, &p);
        // 如果a%p不等于0，若a<p，由p为质数，a,p互质。若a>p,p不等整除a，a,p互质
        if (a % p) printf("%d\n", qmi(a, p - 2, p));
        else puts("impossible");
    }
    return 0;
}

扩展欧几里得算法

扩展欧几里得算法

思路：
裴蜀定理: 对任何整数$a$、$b$，存在整数$x$、$y$，使得$ax+by=(a,b)$， $(a,b)$表示$a$、$b$的最大公因数，令$d=(a,b)$。
若$b=0$，则$d=a$，$x=1$，$y=0$
由数学定理知，$(a,b)=(b,amodb)$。$a$、$b$交换顺序后，则有
$$\begin{gathered} (amodb)x+by=d \\ (amodb)=a-\lfloor \frac{a}{b}\rfloor b \\ (a-\lfloor \frac{a}{b}\rfloor b)x+by=d \\ ax+(y-\lfloor \frac{a}{b}\rfloor x)b=d \end{gathered}$$
根据公式看到，与$b$位置相同的参数的系数对应的为$y$。

代码：

#include<iostream>
using namespace std;

/**
int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}
*/

int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    
    int d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

int main()
{
    int n;
    scanf("%d", &n);
    while (n--)
    {
        int a, b, x, y;
        scanf("%d%d", &a, &b);
        exgcd(a, b, x, y);
        printf("%d %d\n", x, y);
    }
    return 0;
}

线性同余方程

思路：
$\because ax\equiv b(\mathrm{mod}m)，\exists y\in Z$,使得：$ax-my=b$。令$y=-y$,则$ax+my=b$，令$d=(a,m)$，并且$d|b$。
用拓展欧几里得算法求解，$ax+my=d$，$x$、$y$扩大 $\frac{b}{d}$ 倍，即可化为$ax+my=b$。
输出答案必须在 $int$ 范围之内，计算出来的$x$可能超过限制，又
$$ax\mathrm{mod}m=(a\ast (x\mathrm{mod}m))\mathrm{mod}m$$
保险起见，最后的$x\mathrm{mod}m$。
代码：

#include<iostream>
using namespace std;

/**
int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}
*/

int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    
    int d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

int main()
{
    int n;
    scanf("%d", &n);
    while (n--)
    {
        int a, b, m, x, y;
        scanf("%d%d%d", &a, &b, &m);
        int d = exgcd(a, m, x, y);
        if (b % d) puts("impossible");
        else printf("%d\n", (long long)b / d * x % m);
    }
    return 0;
}

中国剩余定理

表达整数的奇怪方式

思路：
先引入中国剩余定理：
用现代数学的语言来说明的话，中国剩余定理给出了以下的一元线性同余方程组：
$$(S):\{\begin{array}{l}x\equiv a_1(\mathrm{mod}{m}_1)\\ x\equiv a_2(\mathrm{mod}{m}_2)\\ x\equiv a_3(\mathrm{mod}{m}_3)\\ ...\\ x\equiv a_n(\mathrm{mod}{m}_n)\end{array}$$
中国剩余定理说明：假设整数$m_1,m_2,...,m_n$两两互质，则对任意的整数：$a_1,a_2,...,a_n$，方程组 $(S)$有解，并且通解可以用如下方式构造得到：

令$M=m_1\times m_2\times m_3\times ...\times m_n=\prod _{i=1}^n{m}_i$，令 M i = M m i , ∀ i ∈ { 1 , 2 , . . . , n } M_i= \cfrac {M}{m_i}, \forall i \in \{1,2,...,n\} Mi​=mi​M​,∀i∈{1,2,...,n}，设$M_i^{-1}$为$M_i$模$m_i$的逆元。

方程组$(S)$的通解形式为：
$$\begin{array}{rl}x& =a_1{M}_1^{-1}{M}_1+a_2{M}_2^{-1}{M}_2+...+a_n{M}_n^{-1}{M}_n+kM\\ & =kM+\sum _{i=1}^n{a}_i{M}_i^{-1}{M}_i,k\in \mathbb{Z}\end{array}$$
进行验证，等式右边对 $m_i$ 取模，除了 $a_i{M}_i^{-1}{M}_i$ 之外的所有项都包含因数 $m_i$，取模结果为0。根据逆元的定义 $M_i^{-1}{M}_i$ 对 $m_i$ 取模结果为1，则$a_i{M}_i^{-1}{M}_i$对$m_i$取模结果为 $a_i$ ,证明 $x$ 确实是 一元线性同余方程组的解。

但本题中给的条件并没有说明$m_i$是互质的，因此不能用上述的方式求得通解。

换一种方式证明：
$$(S):\{\begin{array}{l}x\equiv a_1(\mathrm{mod}{m}_1)\\ x\equiv a_2(\mathrm{mod}{m}_2)\\ x\equiv a_3(\mathrm{mod}{m}_3)\\ ...\\ x\equiv a_n(\mathrm{mod}{m}_n)\end{array}$$
考虑前两个方程：
$$\{\begin{array}{l}x\equiv a_1(\mathrm{mod}{m}_1)\\ x\equiv a_2(\mathrm{mod}{m}_2)\end{array}$$
对方程组进行等价变形：
$$\{\begin{array}{l}x=k_1{a}_1+m_1\\ x=k_2{a}_2+m_2\end{array}$$
联立两个等式，消去$x$，得：
$$\begin{array}{rl}{k}_1{a}_1+m_1& =k_2{a}_2+m_2\\ k_1{a}_1-k_2{a}_2& =m_2-m_1\end{array}$$

$k_1$、$k_2$ 有解等价于 $(a1,a2)|(m_2-m_1)$，令 $d=(a1,a2)$

$k_1$、$k_2$ 通解为：

$$\{\begin{array}{l}{k}_1=k_1+k\frac{a_2}{d}\\ k_2=k_2+k\frac{a_1}{d}\end{array}$$
其中 $k\in \mathbb{Z}$，将 $k_1$ 待入 $x$中，得：

$$\begin{array}{rl}x& =k_1{a}_1+m_1\\ & =(k_1+k\frac{a_2}{d})a_1+m_1\\ & =k_1{a}_1+k\frac{a_1{a}_2}{d}+m_1\\ & =(k_1{a}_1+m_1)+k[a_1,a_2]\end{array}$$
把 $[a1,a2]$ 看作 $a_1$，$k_1{a}_1+m_1$ 看作 $m_1$，得方程的一般形式为：

$$\begin{array}{rl}x& =\underset{更新后的m_1}{\underbrace{k_1{a}_1+m_1}}+k\underset{更新后的a_1}{\underbrace{[a1,a2]}}\\ & =k_1{a}_1+m_1\end{array}$$
则经过$n-1$次迭代，可以将$n$个方程合并为一个方程，$m_1$可以视作$x_1$，最后的 $m_1$就是所求的解。

代码：

#include <iostream>
using namespace std;

typedef long long ll;

ll exgcd(ll a, ll b, ll &x, ll &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    ll d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

int main()
{
    int n;
    cin >> n;
    
    ll a1, m1;
    cin >> a1 >> m1;
    
    for (int i = 0; i < n - 1; i++)
    {
        ll a2, m2, k1, k2;
        cin >> a2 >> m2;
        ll d = exgcd(a1, a2, k1, k2);
        // d | m2 - m1表示有解，否则输出 -1
        if ((m2 - m1) % d)
        {
            puts("-1");
            return 0;
        }
        
        // 此时k1是 k1 * a1 + k2 * a2 = d的解,所以要乘上(m2-m1) / d
        k1 *= (m2 - m1) / d; 
        ll t = a2 / d;
        // 模 t 是因为 k1 = k1 + kt, k1是不断迭代的结果，取模保证k1取比较小的值
        k1 = (k1 % t + t) % t;
        // 更新 m1, m1不断迭代，可以看作方程的解
        m1 = a1 * k1 + m1;
        // 更新a1，a1,a2,...,an的最小公倍数
        a1 = a1 * a2 / d;
    }
    
    cout << (m1 % a1 + a1) % a1<< endl;
    
    return 0;
}

高斯消元

高斯消元解线性方程组

思路：

推导过程与线性代数求方程组的过程一样，主要就是通过初等行变换将增广矩阵变化为最简行阶梯型矩阵。比较系数矩阵与增广矩阵的秩，以及与未知数个数的关系，判断解的情况。在这里就不赘述了，代码中所需要注意的细节在注释里标注的很详细。

代码：

#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;

const int N = 110;
const double eps = 1e-6;
int n;
double a[N][N];

int gauss()
{
    int c, r;
    
    // 表示当前行， r表示当前列
    for (c = 0, r = 0; c < n; c++)
    {
        int t = r;
        // 找到每一行第一个非零元素绝对值最大的行
        for (int i = r; i < n; i++)
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;
        // 当前列第一个元素值为0 则跳至下一列
        if (fabs(a[t][c]) < eps) continue;
        
        // 将绝对值最大的行换到最顶端 最顶端即当前行r
        for (int i = c; i <= n; i++) swap(a[t][i], a[r][i]);
        // 将当前行的首位变成1 当前行的每一个数都除以首位的值 
        // 逆序保证每一项都除以首位的值，否则除首项外每一项都除以的是1
        for (int i = n; i >= c; i--) a[r][i] /= a[r][c];
        // 用当前行将下面所有的列首项消成0
        for (int i = r + 1; i < n; i++)
        {
            if (fabs(a[i][c]) > eps)
            {
                // 逆序保证每一项都除以首位的值，否则初首项外都除以的是1
                for (int j = n; j >= c; j--)
                    a[i][j] -= a[r][j] * a[i][c];
            }
        }
        
        r++;
    }
    
    // 系数矩阵的秩小于未知数的个数n：
    // 	1. 系数矩阵的秩小于增广矩阵的秩，无解
    // 	2. 系数矩阵的秩等于增广矩阵的秩，无穷解
    if (r < n)
    {
        // 系数矩阵的秩小于增广矩阵的秩，无解
        for (int i = r; i < n; i++)
            if (fabs(a[i][n]) > eps)
                return 2;
        
        // 系数矩阵的秩等于增广矩阵的秩，无穷解
        return 1;
    }
    
    // 倒着把答案推出来
    // 系数矩阵的秩等于未知数的个数n，唯一解
    for (int i = n - 1; i >= 0; i -- )
        for (int j = i + 1; j < n; j ++ )
            a[i][n] -= a[i][j] * a[j][n];
    
    return 0;
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n + 1; j++)
            cin >> a[i][j];
    
    int t = gauss();
    if (t == 0)
    {
        for (int i = 0; i < n; i++) 
            // 防止出现 -0.00
            printf("%.2lf\n", fabs(a[i][n]) < eps ? 0 : a[i][n]);
    }
    else if (t == 1) puts("Infinite group solutions");
    else puts("No solution");
    
    return 0;
}

高斯消元解异或线性方程组

思路：

高斯消元解异或方程组的方法如下：

代码：

#include <iostream>
using namespace std;

const int N = 110;
int a[N][N];
int n;

int gauss()
{
    int r, c;
    for (r = c = 0; c < n; c++)
    {
        // 找一个非0行
        int t = r;
        for (int i = r; i < n; i++)
            if (a[i][c])
            {
                t = i;
                break;
            }
        
        // 当前列找不到非0行,下一列
        if (!a[t][c]) continue;
        
        // 交换到最顶端
        for (int i = c; i <= n; i++) swap(a[t][i], a[r][i]);
        // 把下面行的清0
        for (int i = r + 1; i < n; i++)
            // 下面行首个元素为1，才能异或消掉
            if (a[i][c])
                for (int j = n; j >= c; j--)
                    a[i][j] ^= a[r][j];
                    
        r++;
    }
    
    if (r < n)
    {
        for (int i = r; i < n; i++)
            if (a[i][n]) 
                return 2;
        return 1;
    }
    
    for (int i = n - 1; i >= 0; i--)
    {
        for (int j = i + 1; j < n; j++)
            // x ^ a[i][j]a[j][n] = a[i][n]
            // x ^ a[i][j]a[j][n] ^ a[i][j]a[j][n] = a[i][n] ^ a[i][j]a[j][n]
            // x ^ (a[i][j]a[j][n] ^ a[i][j]a[j][n]) = a[i][n] ^ a[i][j]a[j][n]
            // x ^ 0 = a[i][n] ^ a[i][j]a[j][n]
            a[i][n] ^= a[i][j] & a[j][n];
    }
    
    return 0;
}

int main()
{
    cin >> n;
    
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n + 1; j++)
            cin >> a[i][j];
            
    int res = gauss();
    
    if (res == 0)
    {
        for (int i = 0; i < n; i++) printf("%d\n", a[i][n]);
    }
    else if (res == 1) puts("Multiple sets of solutions");
    else puts("No solution");
    
    return 0;
}

求组合数

求组合数 I

思路：
根据组合数的原理，${\complement }_m^n={\complement }_{m-1}^n+{\complement }_{m-1}^{n-1}$，对于$a、b\in [1,2000]$，$b\le a$，只需在$O(a^2)$的时间复杂度内，就可以预处理出所有的组合数，再依次处理每一次的询问，也就是打表。
代码：

#include <iostream>
using namespace std;

const int N = 2010, mod = 1e9 + 7;
int c[N][N];

int main()
{
    for (int i = 0; i < N; i++)
        for (int j = 0; j <= i; j++)
        {
            if (!j) c[i][j] = 1;
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
        }
    
    int n;
    scanf("%d", &n);
    while (n--)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        printf("%d\n", c[a][b]);
    }
    
    return 0;
}

求组合数Ⅱ

思路：

当$a、b$范围特别大时，此时不适合用上面预处理出所有组合数的方式进行求解。根据组合数的公式${\complement }_m^n=\frac{m!}{n!(m-n)!}$，可以通过预处理$m!$、$n!$、$(m-n)!$，再根据求组合数的公式进行计算，时间复杂度为 $O(N\log mod)$ 。

值得注意的是，除以一个数并取模可以转化为乘该数的逆元，再预处理阶乘的同时，也计算阶乘的逆元。记 $f(i)=i!$ ，$p=1000000007$，$p$ 为质数 ，$f(i{)}^{-1}$ 为 $f(i)$ 模 $p$ 的乘法逆元。$f(0)=f(0{)}^{-1}=1$ ，当 $i\ge 1$ 时， 可得递推关系式为：
$$\{\begin{array}{l}f(i)=f(i-1)\times i\mathrm{mod}p\\ f(i{)}^{-1}=f(i-1{)}^{-1}\times i^{-1}\mathrm{mod}p\end{array}$$
接着依次处理每次询问即可。

代码：

#include <iostream>
using namespace std;

typedef long long ll;

const int N = 100010, mod = 1e9 + 7;
// 阶乘以及阶乘的逆元
int fac[N], infac[N];

int qmul(int a, int b, int p)
{
    int res = 1;
    while (b)
    {
        if (b & 1) res = (ll)res * a % p;
        b >>= 1;
        a = (ll)a * a % mod;
    }
    return res;
}

int main()
{
    // 预处理0的阶乘，以及0的阶乘模 mod 的逆元
    fac[0] = infac[0] = 1;
    for (int i = 1; i < N; i++)
    {
        fac[i] = (ll)fac[i - 1] * i % mod;
        infac[i] = (ll)infac[i - 1] * qmul(i, mod - 2, mod) % mod;
    }

    int n;
    scanf("%d", &n);

    while (n--)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        // 两个相乘之后就开始取模，防止超过范围
        printf("%d\n", (ll)fac[a] * infac[b] % mod * infac[a - b] % mod);
    }
    return 0;
}

求组合数Ⅲ

思路：
对于非负整数$a$、$b$，质数 $p$ ，可以用$Lucas$ 定理来求组合数。$Lucas$ 定理求组合数的公式为：
$${\complement }_a^b={\complement }_{(a\mathrm{mod}p)}^{(b\mathrm{mod}p)}\ast {\complement }_{\lfloor a/p\rfloor }^{\lfloor b/p\rfloor }$$
代码：

#include <iostream>
using namespace std;

typedef long long ll;

int p;

int qmul(int a, int b)
{
    int res = 1;
    while (b)
    {
        if (b & 1) res = (ll) res * a % p;
        a = (ll) a * a % p;
        b >>= 1;
    }
    return res;
}

// 朴素法求组合数
int c(int a, int b)
{
    int res = 1;
    for (int i = 1, j = a; i <= b; i++, j--)
    {
        res = (ll) res * j % p;
        res = (ll) res * qmul(i, p - 2) % p;
    }
    return res;
}

int lucas(ll a, ll b)
{
    if (a < p && b < p) return c(a, b);
    return (ll) lucas(a % p, b % p) * lucas(a / p, b / p) % p;
}

int main()
{
    int n;
    cin >> n;
    
    while (n--)
    {
        ll a, b;
        cin >> a >> b >> p;
        cout << lucas(a, b) << endl;
    }
    
    return 0;
}

求组合数Ⅳ

思路：

本题要求输出组合数的真实结果，朴素方法来求组合数的公式为：

$${\complement }_m^n=\frac{m!}{n!(m-n)!}$$

要用到乘法和除法，下面给出一种优化方式，可以仅用乘法求得组合数。

对于非负整数 $a$、$b$，$p_i$为$a$的质因数，则有：

$$a!=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}...p_k^{{\alpha }_k}$$

接下来求 $p_i$ 的个数，设 $f(a,p)$ 为 $a!$ 中质因子 $p$ 的个数 ，则有下面的结论：

$$\begin{array}{rl}f(a,p)& =\lfloor \frac{a}{p}\rfloor +\lfloor \frac{a}{p^2}\rfloor +\lfloor \frac{a}{p^3}\rfloor +...\\ & =p的倍数+p^2的倍数+p^3的倍数+...\end{array}$$

举例验证：$8!=1\times 2\times 3\times 4\times 5\times 6\times 7\times 8$ ，求其中 $2$ 的个数。

• 含 $2$ 的一次方的有 $2、4、6、8$ 四个$2$ 。
• 含 $2$ 二次方有 $4、8$ ，但 $4、8$ 中 $2$ 的一次方已经记过一次了，所以只加二次方中的两个 $2$ 。
• 含 $2$ 三次方有 $8$ ，但 $8$ 中 $2$ 的一次方已经记过一次了，所以只加三次方中的一个 $2$ 。

同理可类推到 $p^k$ 它的幂次中的前 $k-1$ 个 $p$，在计算 $p^1\sim p^{k-1}$ 次数中都已经算过一次。

${\alpha }_i$ 为 分子 $a!$ 中 质因数 $p_i$ 的个数，减去 分母中 $b!(a-b)!$ 中 质因数 $p_i$ 的个数，得 ${\alpha }_i^{\prime }$ 再把所有的质因数相乘，得到的结果就是组合数：

$${\complement }_a^b=\prod _{i=1}^k{p}_i^{{\alpha }_i^{\prime }}$$

代码：

#include <iostream>
#include <vector>

using namespace std;

const int N = 5010;
int primes[N], cnt, sum[N];
bool st[N];

void get_primes(int n)
{
    for (int i = 2; i <= n; i++)
    {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] <= n / i; j++)
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

// 获取n！中p质因子的个数
int get(int n, int p)
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}

// 高精度乘法
vector<int> mul(vector<int> &a, int b)
{
    vector<int> res;
    int t = 0;
    for (int i = 0; i < a.size() || t; i++)
    {
        if (i < a.size()) t += a[i] * b;
        res.push_back(t % 10);
        t /= 10;
    }
    
    // 去掉前导0
    while (res.size() > 1 && res.back() == 0) res.pop_back();
    return res;
}



int main()
{
    int a, b;
    cin >> a >> b;
    
    get_primes(a);
    
    for (int i = 0; i < cnt; i++)
    {
        int p = primes[i];
        sum[i] = get(a, p) - get(b, p) - get(a - b, p);
    }
    
    vector<int> res;
    res.push_back(1);
    
    for (int i = 0; i < cnt; i++)
        for (int j = 0; j < sum[i]; j++)
            res = mul(res, primes[i]);
            
    for (int i = res.size() - 1; i >= 0; i--) printf("%d", res[i]);

    
    return 0;
}

满足条件的01序列

思路：

将寻找满足条件的长度为 $2n$ 的序列的问题，转化为在直角坐标系中，从原点 $(0,0)$ 出发到 $(n,n)$ 的路径，一个路径对应一个 $01$ 序列。假设向右走记为 $0$ ，向上走记为 $1$ 。满足条件的序列要求前缀中 $0$ 的个数不少于 $1$ 的个数，即任意时刻向右走的步数大于向上走的步数， 路径经过的任意一点的坐标 $(x,y)$ 满足 $x\ge y$ ，所以路径都在直线 $y=x$ 上及以下， 不满足条件的路径都会穿过直线 $y=x+1$ ，分析见如下示例：

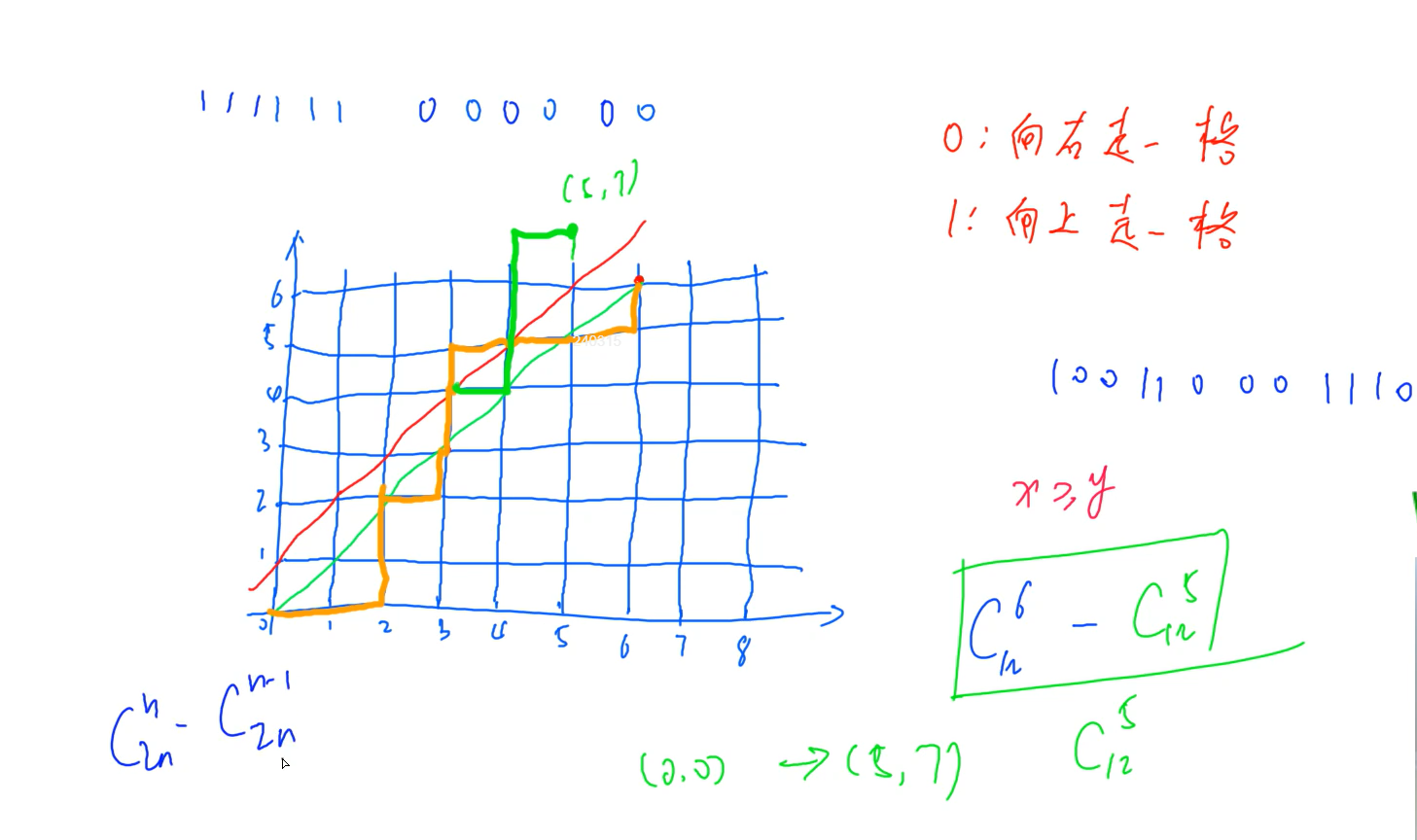
以 $n=6$ 的情况进行分析，将不符合条件的路径在直线 $y=x+1$ 上方的部分以直线 $y=x+1$ 为对称轴做轴对称图形，由几何关系知，终点一定会到达 $(5,7)$ 。到达 $(6,6)$ 的路径总数为 ${\complement }_{12}^6$，不符合条件的路径总数等于 到达 $(5,7)$ 的路径总数，值为 ${\complement }_{12}^5$ ，所以符合条件的路径总数为 ${\complement }_{12}^6-{\complement }_{12}^5$ ，将这一结论推广，得满足条件的长度为 $2n$ 的序列的总数为：

$$\begin{array}{rl}{\complement }_{2n}^n-{\complement }_{2n}^{n-1}& =\frac{(2n)!}{n!n!}-\frac{(2n)!}{(n-1)!(n+1)!}\\ & =\frac{(2n)!(n+1)}{(n+1)!n!}-\frac{(2n)!n}{(n+1)!n!}\\ & =\frac{(2n)!}{(n+1)!n!}\\ & =\frac{1}{n+1}\frac{(2n)!}{n!n!}\\ & =\frac{1}{n+1}{\complement }_{2n}^n\end{array}$$

$\frac{1}{n+1}{\complement }_{2n}^n$ 也就是卡塔兰数 $(Catalannumber)$ 。

代码：

#include <iostream>
using namespace std;

typedef long long ll;

const int mod = 1e9 + 7;

int qmul(int a, int k)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (ll) res * a % mod;
        k >>= 1;
        a = (ll) a * a % mod;
    }
    return res;
}

int main()
{
    int n;
    cin >> n;
    
    int a = 2 * n, b = n;
    int ans = 1;
    
    for (int i = 1, j = a; i <= b; i++, j--)
    {
        ans = (ll) ans * j % mod;
        ans = (ll) ans * qmul(i, mod - 2) % mod;
    }
    
    ans = (ll)ans * qmul(n + 1, mod - 2) % mod;
    
    cout << ans << endl;
    
    return 0;
}

容斥原理

能被整除的数

思路：

首先，从一个例子引入容斥原理：

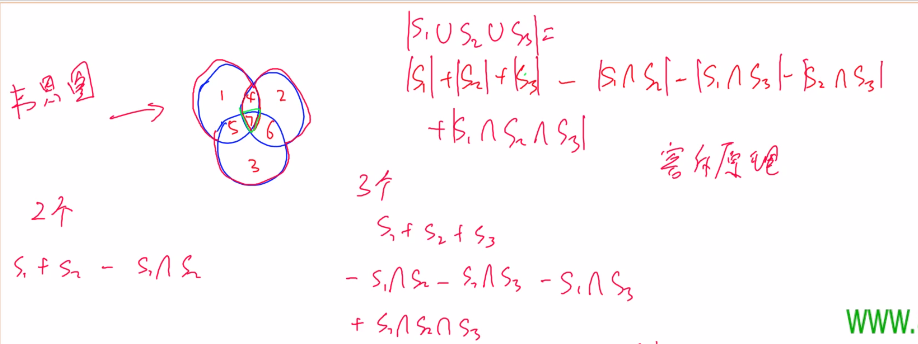
本题求解的思路与上一个例子中求解面积的思路类似，假设 $S_i$ 为 $1\sim n$ 中能被 $p_i$ 整除的数的集合，则 $|S_i|$ 表示集合 $S_i$ 的元素个数，且 $|S_i|=\lfloor \frac{n}{p}\rfloor$ ， $1\sim n$ 中能被 $p_i$ 、$p_j$整除的数的集合表示为 $S_i\cap S_j$ ，$|S_i\cap S_j|=\lfloor \frac{n}{p_i{p}_j}\rfloor$ ，推广得：

$1\sim n$ 中能被 $p_i$ 、$p_j$ 、$p_k$ … 整除的数的集合表示为 $S_i\cap S_j\cap S_k...$ ，$|S_i\cap S_j\cap S_k...|=\lfloor \frac{n}{p_i{p}_j{p}_j...}\rfloor$ 。$|S_i\cup S_j...\cup S_n|$ 表示 $1\sim n$ 中能被 $p_i$ 、$p_j$ 、$p_k$ … 中至少一个数整除的数的个数，最终的结果为：

$$|S_i\cup S_j...\cup S_n|=\sum _i|S_i|-\sum _{i,j}|S_i\cap S_j|+\sum _{i,j,k}|S_i\cap S_j\cap S_k|+...+(-1{)}^{n-1}\sum _{i,j,k...n}|S_i\cap S_j\cap S_k...\cap S_n|$$

由组合计数的原理知，一共有 $2^n-1$ 个集合，时间复杂度为 $O(2^n)$ ，可以枚举一个 $n$ 位的二进制数，第 $m$ 位为 $1$ 表示包括这个集合，二进制数中 $1$ 的个数为奇数时，系数为 $1$ ，否则为 $-1$ 。

代码：

#include <iostream>
using namespace std;

typedef long long ll;

const int N = 20;
int p[N];

int main()
{
    int n, m;
    cin >> n >> m;
    
    int ans = 0;
    
    for (int i = 0; i < m; i++) cin >> p[i];
    
    for (int i = 1; i < 1 << m; i++)
    {
        // t为质因数的乘积， cnt为i中1的个数。
        int t = 1, cnt = 0;
        for (int j = 0; j < m; j++)
        {
            if (i >> j & 1) 
            {
                cnt++;
                // 质数乘积大于n, 就不用再考虑了
                if ((ll)t * p[j] > n)
                {
                    t = -1;
                    break;
                }
                t *= p[j];
            }
        }
        
        if (t != -1)
        {
            if (cnt % 2) ans += n / t;
            else ans -= n / t;
        }
    }
    
    cout << ans << endl;
    
    return 0;
}

博弈论

Nim游戏

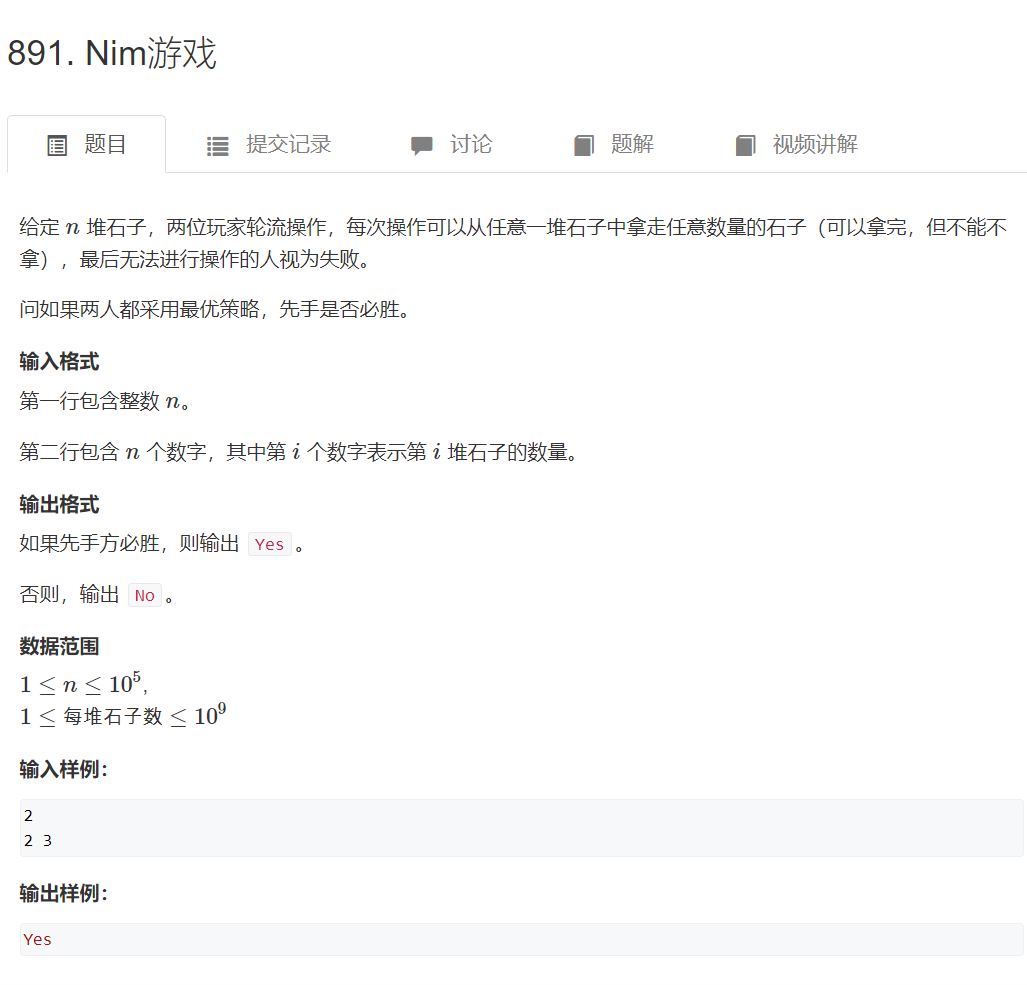
思路：

给定 $N$ 堆物品，第i堆物品有 $A_i$ 个。两名玩家轮流行动，每次可以任选一堆，取走任意多个物品，可把一堆取光，但不能不取。取走最后一件物品者获胜。两人都采取最优策略，问先手是否必胜。

我们把这种游戏称为 NIM 博弈。把游戏过程中面临的状态称为局面。整局游戏第一个行动的称为先手，第二个行动的称为后手。若在某一局面下无论采取何种行动，都会输掉游戏，则称该局面必败。
所谓采取最优策略是指，若在某一局面下存在某种行动，使得行动后对面面临必败局面，则优先采取该行动。同时，这样的局面被称为必胜。我们讨论的博弈问题一般都只考虑理想情况，即两人均无失误，都采取最优策略行动时游戏的结果。

NIM博弈不存在平局，只有先手必胜和先手必败两种情况。

定理： NIM博弈先手必胜，当且仅当 $A_1\oplus A_2\oplus \dots \oplus A_n\ne 0$

为方便证明，引入两种状态：

• 先手必胜状态：通过变换可以变为必败状态的状态，$A_1\oplus A_2\oplus \dots \oplus A_n\ne 0.$
• 先手必败状态：通过变换不可以变为必败状态的状态，$A_1\oplus A_2\oplus \dots \oplus A_n=0.$

先手必胜状态:

假设 $A_1\oplus A_2\oplus \dots \oplus A_n=x\ne 0$，$x$ 的二进制表示中最高位 $1$ 在第 $k$ 位，$A_1,A_2...A_n$ 中 必然有一个数 $A_i$ 的第 $k$ 位为 $1$ ，则有 $A_i\oplus x<A_i$，从第 $i$ 堆中拿走 $A_i-(A_i\oplus x)$个，得第 $i$ 堆中剩余个数:
$$A_i^{\prime }=A_i-(A_i-(A_i\oplus x))=A_i\oplus x$$

接下来的状态：

$$\begin{array}{rl}{A}_1\oplus A_2\oplus ...\oplus A_i^{\prime }...\oplus A_n& =A_1\oplus A_2\oplus ...\oplus A_i\oplus x...\oplus A_n\\ & =A_1\oplus A_2\oplus \dots \oplus A_n\oplus x\\ & =x\oplus x\\ & =0\end{array}$$

可以变为必败状态，因此处于先手必胜状态的先手在理想状态下必胜。

先手必败状态：

假设 $A_1\oplus A_2\oplus \dots \oplus A_n=x=0$，经过理想变换得第 $i$ 堆中剩余个数 $A_i^{\prime }$ 。

接下来的状态：

$$\begin{array}{rl}{A}_1\oplus A_2\oplus ...\oplus A_i^{\prime }...\oplus A_n& =0\\ & =A_1\oplus A_2\oplus ...\oplus A_i...\oplus A_n\end{array}$$

得 $A_i^{\prime }=A_i$ ，又 $A_i^{\prime }\ne A_i$ ，矛盾，因此先手必败状态无法通过变换变为必败状态，因此处于先手必败状态的先手在理想状态下必败。

代码

#include <iostream>
uisng namespace std;

int main()
{
    int n, res = 0;
    scanf("%d", &n);
    
    while (n--)
    {
        int x;
        scanf("%d", &x);
        res ^= x;
    }
    
    puts(res ? "Yes" : "No");
        
    return 0;
}

台阶-Nim游戏

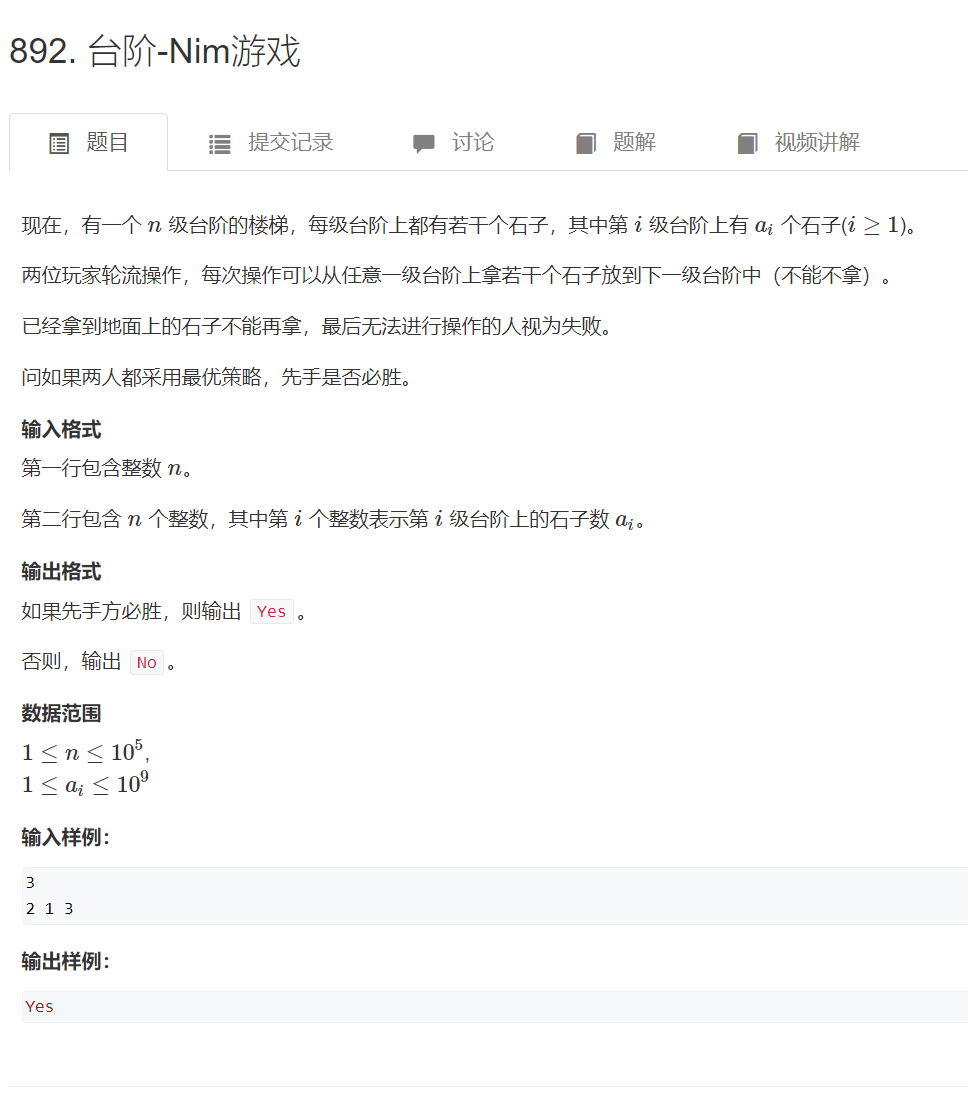
思路：

台阶 Nim 游戏一种可行的解法是判断奇数台阶石子数异或值不等于0，则先手必胜。在此状态下，先手总有办法通过变换使奇数台阶石子数异或值等于0，此时，如果后手拿了奇数台阶的石子，先手可以通过移动其他奇数台阶的石子使奇数台阶石子数异或值等于0，如果后手拿了偶数台阶的石子，先手可以通过移动相同数量的石子使奇数台阶石子数异或值等于0，因此先手必胜。

对样例进行验证：

第一步先手可将3号台阶的1个石子移动到2号台阶，此时奇数台阶石子数异或值等于0，后手接下来有三种走法：

• 拿2号台阶的石子放到1号台阶，先手下一步可以将相同数量的石子放到地面，奇数台阶石子数异或值等于0
• 拿1号台阶的石子放到地面，先手可将相同数量的石子从3号台阶放到2号台阶，奇数台阶石子数异或值等于0
• 拿3号台阶的石子放到2号台阶，先手可将相同数量的石子从1号台阶放到地面，奇数台阶石子数异或值等于0

因此，只要一开始奇数台阶石子数异或和不等于0，先手总能通过移动石子使奇数台阶石子数异或和等于0，因此先手必胜。

代码：

#include <iostream>
using namespace std;

int main()
{
    int n, res = 0;
    scanf("%d", &n);
    
    for (int i = 1; i <= n; i++)
    {
        int x;
        scanf("%d", &x);
        if (i % 2) res ^= x;
    }
    
    puts(res ? "Yes" : "No");
    return 0;
}

集合-Nim游戏

思路：

与上题不同的是，每次拿取的石子数量是有限制的，包含于集合 $S$ 中。从当前状态拿取不同的石子接下来的状态是可以追溯可以枚举的，可以看作从当前状态可以用箭头指向多个状态，类似于有向图，因此本题也是一个有向图游戏问题。

有向图游戏：

给定一个有向无环图，图中有一个唯一的起点，在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动，每次可以移动一步，无法移动者判负。该游戏被称为有向图游戏。

任何一个公平组合游戏都可以转化为有向图游戏。具体方法是，把每个局面看成图中的一个节点，并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。

为了便于分析有向图游戏问题，引入两个概念：

• $Mex$ 运算
• $SG$ 函数

$Mex$ 运算:

设 $S$ 表示一个非负整数集合。定义 $mex(S)$ 为求出不属于集合 $S$ 的最小非负整数的运算，即：

m e x ( S ) = m i n { x } mex(S) = min\{x\} mex(S)=min{x}, $x$ 属于自然数，且 $x$ 不属于 $S$。

$SG$函数：

在有向图游戏中，对于每个节点 $x$ ，设从 $x$ 出发共有 $k$ 条有向边，分别到达节点 $y1,y2,\dots ,yk$ ，定义 $SG(x)$ 为 $x$ 的后继节点 $y1,y2,\dots ,yk$ 的 $SG$ 函数值构成的集合再执行 $mex(S)$ 运算的结果，即：

S G ( x ) = m e x ( { S G ( y 1 ) , S G ( y 2 ) , … , S G ( y k ) } ) SG(x) = mex(\{SG(y1), SG(y2), …, SG(yk)\}) SG(x)=mex({SG(y1),SG(y2),…,SG(yk)})

特别地，整个有向图游戏 $G$ 的 $SG$ 函数值被定义为有向图游戏起点 $s$ 的 $SG$ 函数值，即 $SG(G)=SG(s)$ 。

定理：
有向图游戏的某个局面必胜，当且仅当该局面对应节点的 $SG$ 函数值大于0。
有向图游戏的某个局面必败，当且仅当该局面对应节点的 $SG$ 函数值等于0。

下面举个例子更好理解：

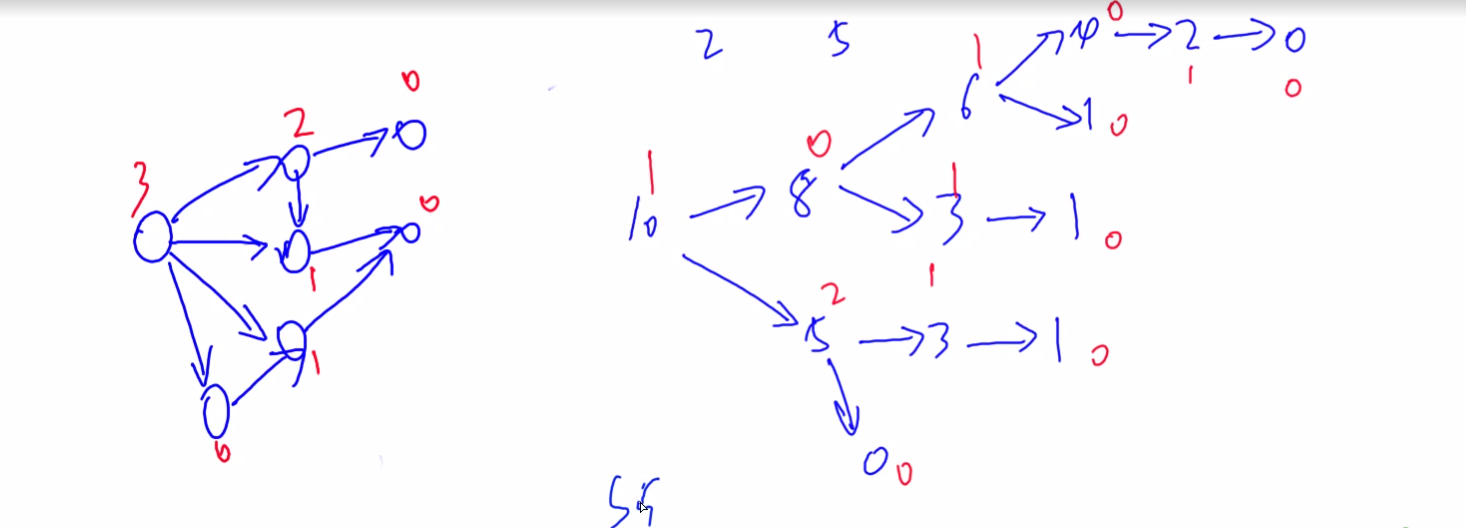
有向图游戏的和的 $SG$ 函数值等于它包含的各个子游戏 $SG$ 函数值的异或和，即：
$$SG(G)=SG(G_1)\oplus SG(G_2)\oplus \dots \oplus SG(G_m)$$

证明过程与上题类似。

对于有向图问题计算 $SG$ 值问题可以用到记忆化搜索，保证每个节点最多只遍历一次，时间复杂度为 $O(nk)$ 。

代码：

#include <iostream>
#include <cstring>
#include <set>
using namespace std;

const int N = 110, M = 10010;

// s表示数字集 f[i]表示数量为i的石子的sg值
int s[N], f[M];
int n, k;

int sg(int x)
{
    if (f[x] != -1) return f[x];
    
    set<int> S;
    for (int i = 0; i < k; i++)
        if (x >= s[i]) S.insert(sg(x - s[i]));
    
    for (int i = 0; ; i++)
        if (!S.count(i))
            return f[x] = i;
}

int main()
{
    cin >> k;
    for (int i = 0; i < k; i++) cin >> s[i];
    
    memset(f, -1, sizeof f);
    
    int res = 0;
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        int x;
        cin >> x;
        res ^= sg(x);
    }
    
    puts(res ? "Yes" : "No");
    
    return 0;
}

拆分-Nim游戏

思路：

假设一个局面为 $a_i$ ，根据题意可以拆分为两个局面，设为 $(b_i,b_j)...$，且 $|a_i|>|b_i|\ge |b_j|$，根据有向图游戏的性质，$sg(a_i)=sg(b_i)\oplus sg(b_j)$，局面 $a_i$ 可以分为 $|a_i{|}^2$ 种不同的局面，局面 $a_i$ 划分的所有局面的 $sg$ 值异或起来的值就是 $sg(a_i)$，最后的结果为：

$$sg(a)=sg(a_1)\oplus sg(a_2)\oplus sg(a_2)\oplus ...\oplus sg(a_n)$$

若 $sg(a)\ne 0$ ，先手必胜，否则必败。

代码：

#include <iostream>
#include <cstring>
#include <set>
using namespace std;

const int N = 110;
int f[N];

int sg(int x)
{
    if (f[x] != -1) return f[x];
    
    set<int> s;
    
    for (int i = 0; i < x; i++)
        for (int j = 0; j <= i; j++)
            s.insert(sg(i) ^ sg(j));
            
    for (int i = 0; ; i++)
    {
        if (!s.count(i))
            return f[x] = i;
    }
}

int main()
{
    int n, res = 0;
    cin >> n;
    
    memset(f, -1, sizeof f);
    
    for (int i = 0; i < n; i++)
    {
        int x;
        cin >> x;
        res ^= sg(x);
    }
    
    puts(res ? "Yes" : "No");
    
    return 0;
    
}