插值(Interpolation)

最新推荐文章于 2024-04-22 21:00:47 发布
最新推荐文章于 2024-04-22 21:00:47 发布
阅读量645 收藏 1
点赞数
分类专栏： 数模 文章标签： 学习 Powered by 金山文档
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_51831223/article/details/128760172
版权

插值

当数据不足以支撑分析时，可使用插值，“模拟产生”一些新的但又比较靠谱的值来满足需求。

对于给定的(n+1)个插值节点,,,和对应的函数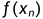值,,,进行插值。

拉格朗日插值(Lagrange interpolation)

n次Lagrange插值多项式

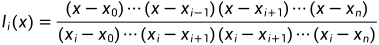
牛顿插值(Newton's interpolation)

k阶差商

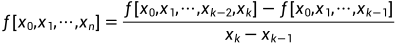
n次牛顿插值多项式

牛顿插值法的计算过程具有继承性。牛顿插值法每次插值只和前n项的值有关，这样每次只要在原来的函数上添加新的项，就能够产生新的函数。

拉格朗日插值和牛顿插值均存在龙格现象（Runge phenomenon）。高次插值会产生龙格现象，即在两端处波动极大,产生明显的震荡。a problem of oscillation at the edges of an interval that occurs when using polynomial interpolation with polynomials of high degree over a set of equispaced interpolation points. 在不熟悉曲线运动趋势的前提下，不要轻易使用高次插值。

拉格朗日插值和牛顿插值仅仅要求插值多项式在插值节点处与被插函数有相等的函数值，而这种插值多项式却不能全面反映被插值函数的性态。在许多实际问题中，不仅要求插值函数与被插值函数在所有节点处有相同的函数值，它也需要在一个或全部节点上插值多项式与被插函数有相同的低阶甚至高阶的导数值。

分段三次Hermite插值（Piecewise Cubic Hermite Interpolating Polynomial）

数值分析：插值与拟合 - 简书 (jianshu.com)

三次样条插值（Cubic spline data interpolation ）

Cubic spline Interpolation - GeeksforGeeks

清风数学建模笔记

weixin_51831223
关注
  • 0
    点赞
  • 踩
  • 1
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
数学建模常见算法：插值算法
smlyor的博客
10-04 7840
数学建模常用算法：插值算法
常用的三种插值算法
热门推荐
知识搬运工的博客
05-27 10万+
在做数字图像处理时，经常会碰到小数象素坐标的取值问题，这时就需要依据邻近象素的值来对该坐标进行插值。比如做图像的几何校正，也会碰到同样的问题。 1、最近邻插值法（Nearest Neighbour Interpolation） 这是最简单的一种插值方法，不需要计算，在待求象素的四邻象素中，将距离待求象素最近邻的像素灰度赋给待求象素。设为待求象素坐标(x+u,y+v) ...
数学建模中的插值问题
最新发布
2401_83703893的博客
04-22 276
长，而且极易碰到天花板技术停滞不前！**
几种常见的插值方法
南城以北的博客
08-09 8540
插值和拟合的区别在于插值方法可以确保通过已知数据点，因此在这些点上的结果是准确的，但在已知数据点之外的区域可能不准确；而拟合方法是找到一个整体的近似描述，可以在已知数据点之外的区域进行预测或估计，但结果可能有一定的误差。插值可以被认为是拟合的一种方法。
4.1 插值概念与基础理论
tang7mj的博客
04-21 3700
插值是数值分析中重要的概念之一，主要用于根据已知数据点构造一个函数，使得该函数在这些数据点上与给定函数或数据完全一致或者足够接近。插值多项式的唯一性：给定一组数据点，对于一次或更高次的插值多项式，是否存在唯一的解，或者说该解是否唯一？插值多项式的存在性：对于一组数据点，是否存在一个次数不超过给定值的插值多项式？插值多项式的构造：如何构造插值多项式，通常采用的是拉格朗日插值或牛顿插值方法？插值误差的估计：如何估计插值多项式的误差，通常采用的是拉格朗日余项或牛顿余项公式？
科学计算概论 07_插值 Interpolation.zip-综合文档
05-19
《科学计算概论 07_插值 Interpolation》是一个关于科学计算中插值方法的专题，主要探讨了如何在给定数据点之间构建连续函数，以近似地代表这些点之间的关系。插值是数值分析中的核心概念，广泛应用于各种科学与工程...
科学计算概论-chap07_插值 Interpolation-综合文档
05-22
《科学计算概论》是关于计算方法的基础教材，其中第7章主要讲解了插值（Interpolation）这一重要概念。插值是数值分析中的核心内容，它涉及到如何通过已知的一组离散数据点来构造一个函数，使得该函数在这些数据点上...
interpolation_Arcpy_批量插值_
10-03
`interpolation_Arcpy_批量插值_`这个标题表明我们将探讨如何使用Python中的`arcpy`模块进行批量的空间插值操作。`arcpy`是Esri公司开发的Geoprocessing工具包，它提供了与ArcGIS Desktop和ArcGIS Pro交互的接口，...
interpolation.zip_Chebyshev_chebyshev插值_interpolation matlab
07-15
3个插值方法matlab代码,monomial的,lagrange的,chebyshev的
interpolation.rar_buriedzpm_插值
07-14
本程序“interpolation.rar_buriedzpm_插值”专注于两种插值技术：分段线性插值和朗格朗日插值。这两种方法都有其独特的应用场景和优势，下面我们将详细探讨它们。 首先，我们来理解分段线性插值。分段线性插值是将...
数值计算基础（三）插值篇
staywithmoon的博客
03-12 1335
概要：文章介绍了插值的概念和三种插值方法（Lagrange 插值、Newton 插值、Hermite 插值、三次样条插值） 1 插值 1.1 插值目的 函数的插值与逼近是研究用简单函数为各 种离散数据建立连续的数学模型；为各种 非有理函数提供好的逼近，使它们既能达 到精确度要求又使计算量尽可能小。 1.2 插值定义 在函数y=f(x) 定义区间 a,b 的一系列节点 x0, x1,….xn处测得函数值 y0=f(x0)，y1=f(x1)，yn=f(xn) 由此构造一个简单易算的近似函数P(x)，满足 P(x
一些插值法及理解
zhangyue_lala的博客
03-21 6万+
插值法就是一个从已知点近似计算未知点的近似计算方法，即构造一个多项式函数，使其通过所有已知点，然后用求得的函数预测位置点。下面记录几种最近学到的插值法以及它们的试用条件及优缺点，简单说一下自己对于插值多项式构造的理解。 1.Lagrange插值法 2.Newton插值法 3.Neville插值法 4.分段线性插值法 5.条样插值法
插值法
Hello World
12-09 2万+
1、问题提出：生产实践中往往出现的问题是，给出一批离散样点，要求作出一条通过这些点的光滑曲线，以便满足设计要求或者进行加工，反映在数学上，即已知函数在一些点上的值，寻求它的分析表达式。因为由函数的表格形式不能直接得出表中未列点处的函数值，也不便于研究函数的性质；此外虽然有些函数有表达式，但因式复杂，不易计算和进行理论分析，也需要构造一个简单函数来近似它。 解决方法： （1）插值法——给出函数f(x)的一些样点值，选定一个便于计算的函数形式，如多项式、分式线性函数及三角多项式等，要求它通过已知样点，由此确定.
第三讲 插值算法
qq_63767210的博客
08-11 3862
第三讲 插值算法
插值方法总结
vicky_white的博客
05-11 1万+
插值方法总结 转自 ： https://blog.csdn.net/jia_zhengshen/article/details/11802147 “牛眼”现象现象是某些偏大或偏百小的数据在插值过程中,所形成的以插值点为圆度心的圈状现象。造成问这一现象的原因是插值区域监测井分布不均匀,而IDW插值过程中仅答以距离为权重,忽略了方位专等其他因素的影响,所以插值结果会与属实测值有较大偏差. 1、最邻近元法 　　这是最简单的一种插值方法，不需要计算，在待求象素的四邻象素中，将距离待求象素最近...
Matlab中插值函数汇总和使用说明
yongqing2010的专栏
09-26 8715
转载http://blog.sciencenet.cn/blog-457143-679275.html Matlab中插值函数汇总和使用说明 MATLAB中的插值函数为interp1，其调用格式为：  yi= interp1(x,y,xi,'method')            其中x，y为插值点，yi为在被插值点xi处的插值结果；x,y为向量， 'meth
【图像处理】详解 最近邻插值、线性插值、双线性插值、双三次插值
闻韶
04-28 3万+
插值 (Interpolation)，通常指内插，既是离散数学名词，也是图像处理术语，二者的联系十分密切。作为图像放缩 (Scale) 的手段，常见的传统插值方法有：最近邻插值 (Nearest Neighbour Interpolation)、线性插值(Linear Interpolation)、双线性插值 (Bilinear Interpolation)、双三次插值 (Bicubic interpolation) 等乃至更高阶的线性插值方法。
pandas.interpolate中spline（三次样条插值法）的用法
Suiiiii的博客
03-01 9394
from pandas import read_csv from pandas import datetime from matplotlib import pyplot num_of_order = 3 def parser(x): return datetime.strptime('190'+x, '%Y-%m') series = read_csv('shampoo.csv',h...
interpolation
06-03
interpolation（插值）是指在数据点之间进行估计或者预测。在可视化中，插值可以用于平滑曲线或图像、填充缺失数据等。 在 Python 中，matplotlib 和 seaborn 库中的许多绘图函数都提供了 interpolation 参数，可用于控制插值方法。常用的插值方法包括： - ‘nearest’：最近邻插值，即使用最近的数据点作为估计值。 - ‘linear’：线性插值，即使用两个最近的数据点之间的线性关系进行估计。 - ‘cubic’：三次样条插值，即使用三次多项式拟合数据点来进行估计。 - ‘spline’：样条插值，是一种平滑的插值方法，可以使用一条平滑的曲线来拟合数据点。 下面是一个使用插值方法绘制函数图像的示例代码： ```python import numpy as np import matplotlib.pyplot as plt # 生成 x 和 y 数据 x = np.linspace(0, 2*np.pi, 21) y = np.sin(x) # 绘制原始数据的散点图 plt.scatter(x, y, color='r') # 绘制插值曲线 x_new = np.linspace(0, 2*np.pi, 100) y_new = np.interp(x_new, x, y) plt.plot(x_new, y_new, color='b', linestyle='--', linewidth=2, label='interpolation') # 显示图像 plt.legend() plt.show() ``` 在上面的代码中，使用 np.interp() 函数对原始数据进行插值，生成新的 x 和 y 数据，然后使用 plot() 函数绘制插值曲线。在 plot() 函数中，linestyle 参数设置线条样式，linewidth 参数设置线条宽度，label 参数设置图例标签。最后使用 legend() 函数添加图例，show() 函数显示图像。 您可以根据需要修改插值方法和其他参数，生成符合您需求的图像。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值