2021年hznu寒假集训第九天 最短路入门

2021年hznu寒假集训第九天

最短路相关概念

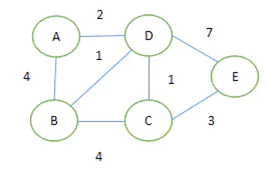
Floyd

我们定义一个数组 dis[k][x][y] ，表示只允许经过结点 V1 到 Vk ，结点 x 到结点 y 的最短路长度。

很显然， dis[n][x][y] 就是最终结点 x 到结点 y 的最短路长度。

dis[0][x][y] 是 x 与 y 的边权，或者 0 ，或者 inf （当 x 与 y 间有直接相连的边的时候，为它们的边权；当 x = y 的时候为零，因为到本身的距离为零；当 x 与 y 没有直接相连的边的时候，为 inf ）

dis[k][x][y] = min(dis[k-1][x][y], dis[k-1][x][k]+dis[k-1][k][y]) （ dis[k-1][x][y] 为不经过 k 点的最短路径，而 dis[k-1][x][k]+dis[k-1][k][y] 为经过了 k 点的最短路）。

上面两行都显然是对的，所以说这个做法空间是 O(𝑁^3) ，我们需要依次增加问题规模（ 从 1 到 n ），判断任意两点在当前问题规模下的最短路。

for (k = 1; k <= n; k++) {
	for (i = 1; i <= n; i++) {
	     for (j = 1; j <= n; j++) {
	            dis[k][i][j] = min(dis[k - 1][i][j], dis[k - 1][i][k] + dis[k - 1][k][j]);     
	     }   
	 } 
}

因为第一维对结果无影响，我们可以发现数组的第一维是可以省略的，于是可以直接改成 dis[x][y] = min(dis[x][y], dis[x][k]+dis[k][y]) 。

for (k = 1; k <= n; k++) {
	for (i = 1; i <= n; i++) {
	    for (j = 1; j <= n; j++) {
			dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
			}
	}
}

时间复杂度为 O(N^3) ，空间复杂度为 O(N^3) 。
用来求任意两个结点之间的最短路的。
复杂度比较高，但是常数小，容易实现。
适用于任何图，不管有向无向，边权正负，但是最短路必须存在（不能有个负环）。

Dijkstra

只适用于非负权图，但是时间复杂度非常优秀。也是用来求单源最短路径的算法。
主要思想是，将结点分成两个集合：已确定最短路长度的，未确定的。
一开始第一个集合里只有 S (源点)。
然后重复这些操作：
1.对那些刚刚被加入第一个集合的结点的所有出边执行松弛操作。
2.从第二个集合中，选取一个最短路长度最小的结点，移到第一个集合中。
对那些刚刚被加入第一个集合的结点的所有出边执行松弛操作。
从第二个集合中，选取一个最短路长度最小的结点，移到第一个集合中。
直到第二个集合为空，算法结束。

板子一、

板子二、

void dijkstra(int s) {
	memset(d, 0x3f, sizeof(d));
	memset(vis, 0, sizeof(vis));
	d[s] = 0;
	while (1) {
		int k=-1,minn=0x3f3f3f3f;
		for (int j = 1;j <= n;j++) {
			if (!vis[j] && d[j] < minn) {
				k = j;
				minn = d[j];
			}
		}
		if (k==-1)return;
		vis[k] = 1;
		for (int j = 1;j <= n;j++) {
			d[j] = min(d[j], d[k] + mp[k][j]);	
		}
	}
}

两种板子本质上都是d[j] = min(d[j], d[k] + mp[k][j])
第二个板子的好处是加一个d[0]的点不会影响到原算法的执行，因为k的赋值是-1，而第一个板子的问题是x的赋值是0.
这个问题在昂贵的聘礼就可以体现。

SPFA

虽然在大多数情况下 SPFA 跑得很快，但其最坏情况下的时间复杂度为 O( NM ) ，将其卡到这个复杂度也是不难的，所以要谨慎使用（在没有负权边时最好使用 Dijkstra 算法，在有负权边且题目中的图没有特殊性质时，若 SPFA 是标算的一部分，题目不应当给出 Bellman-Ford 算法无法通过的数据范围）。

这时候来一个SPFA已死就很好玩。
在非负边权的图中，随手卡 SPFA 已是业界常识。在负边权的图中，不把 SPFA 卡到最慢就设定时限是非常不负责任的行为，随便搞个网格图，菊花图就可，当然，二者结合就更棒了。而卡到最慢就意味着 SPFA 和传统 Bellman Ford 算法的时间效率类似，而后者的实现难度远低于前者。
著名的几种优化纯粹是为了把这块内容补充的详尽一点，来源矢口乎

LLL 优化：每次将入队结点距离和队内距离平均值比较，如果更大则插入至队尾。
Hack：向 1 连接一条权值巨大的边，这样 LLL 就失效了。

SLF 优化：每次将入队结点距离和队首比较，如果更大则插入至队尾。
Hack：使用链套菊花的方法，在链上用几个并列在一起的小边权边就能欺骗算法多次进入菊花。

SLF 带容错：每次将入队结点距离和队首比较，如果比队首大超过一定值则插入至队尾。
Hack：如果边权之和很小的话似乎没有什么很好的办法，因为令边权之和为 ，那么令容错值为 W^1/2，总复杂度似乎接近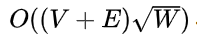
。我不确定这个复杂度对不对，但是 SPFA 确实在边权和小的时候跑得蛮不错的。所以卡法是卡 SLF 的做法，并开大边权，总和最好超过10¹²。

mcfx 优化：在第[L,R]次访问一个结点时，将其放入队首，否则放入队尾。通常取L=2,R=V^1/2 。
Hack：网格图表现优秀，但是菊花图表现很差。
P.S. 此优化与 SLF 带容错一起使用有更好的效果，可以使所需要的边权上升许多。
SLF + swap：每当队列改变时，如果队首距离大于队尾，则交换首尾。

这个 SLF 看起来很弱，但却通过了所有 Hack 数据。而且，非常难卡。

BellMan-Ford

与Dijkstra的区别
bellman可以用于负环，dijkstra不行。
bellman在不存在负环的情况下，进行了n-1次所有边的更新操作后每个节点的最短距离都确定了，再用所有边去更新一次不会改变结果。而如果存在负环，最后再更新一次会改变结果。原因是之前是假定了起点的最短距离是确定的并且是最短的，而又负环的情况下这个假设不再成立。
如果卡最大复杂度的情况下，BellMan的时间复杂度会很高，而dijkstra却不会受到太大的影响。
Dijkstra的本质是贪心，每次在剩余节点中找到离起点最近的节点放到队列中，并用来更新剩下的节点的距离，再将它标记上表示已经找到到它的最短路径，以后不用更新它了。这样做的原因是到一个节点的最短路径必然会经过比它离起点更近的节点，而如果一个节点的当前距离值比任何剩余节点都小，那么当前的距离值一定是最小的。

Bellman-ford的算法解析及优化

最短路的几个算法都是通过第三个点形成的两条边距离来取代原来from->to边的距离。

const int inf=0x3f3f3f;
const int N=10000;
int v[N],u[N],w[N];//起点，终点，权值
int dis[N];//和dijkstra大差不差
int m,n;//边数，点数
memset(dis,inf,sizeof dis);
dis[1]=0;
//核心代码
int bak[N];
for(int k = 1; k <= n - 1; k++){//因为在一个含有 n 个顶点的图中，任意两个顶点之间的最短路径最多包含 n - 1边
	for (int i = 1; i <= n; i++) bak[i] = dis[i]; //记录当前dis值
    for(int i = 1; i <= m; i++)//将每一条边都松弛一遍，每个dis都更新一下
        if(dis[v[i]] > dis[u[i]] + w[i])
            dis[v[i]] = dis[u[i]] + w[i];
	int check=0;
	for(int i=1;i<=n;i++){
		if (bak[i] != dis[i]) {
    	        check = 1;
            	break;
	}
	if (!check) break; //提前跳出循环
}
//检测负权回路
int flag = 0;

for(int i = 1; i <= m; i++)
   if(dis[v[i]] > dis[u[i]] + w[i]) 
       flag = 1;
if(flag == 1)
   printf("此图是负权回路");