1246：膨胀的木棍——二分+数学

【题目描述】
当长度为L的一根细木棍的温度升高n度，它会膨胀到新的长度L’=(1+n*C)*L，其中C是热膨胀系数。

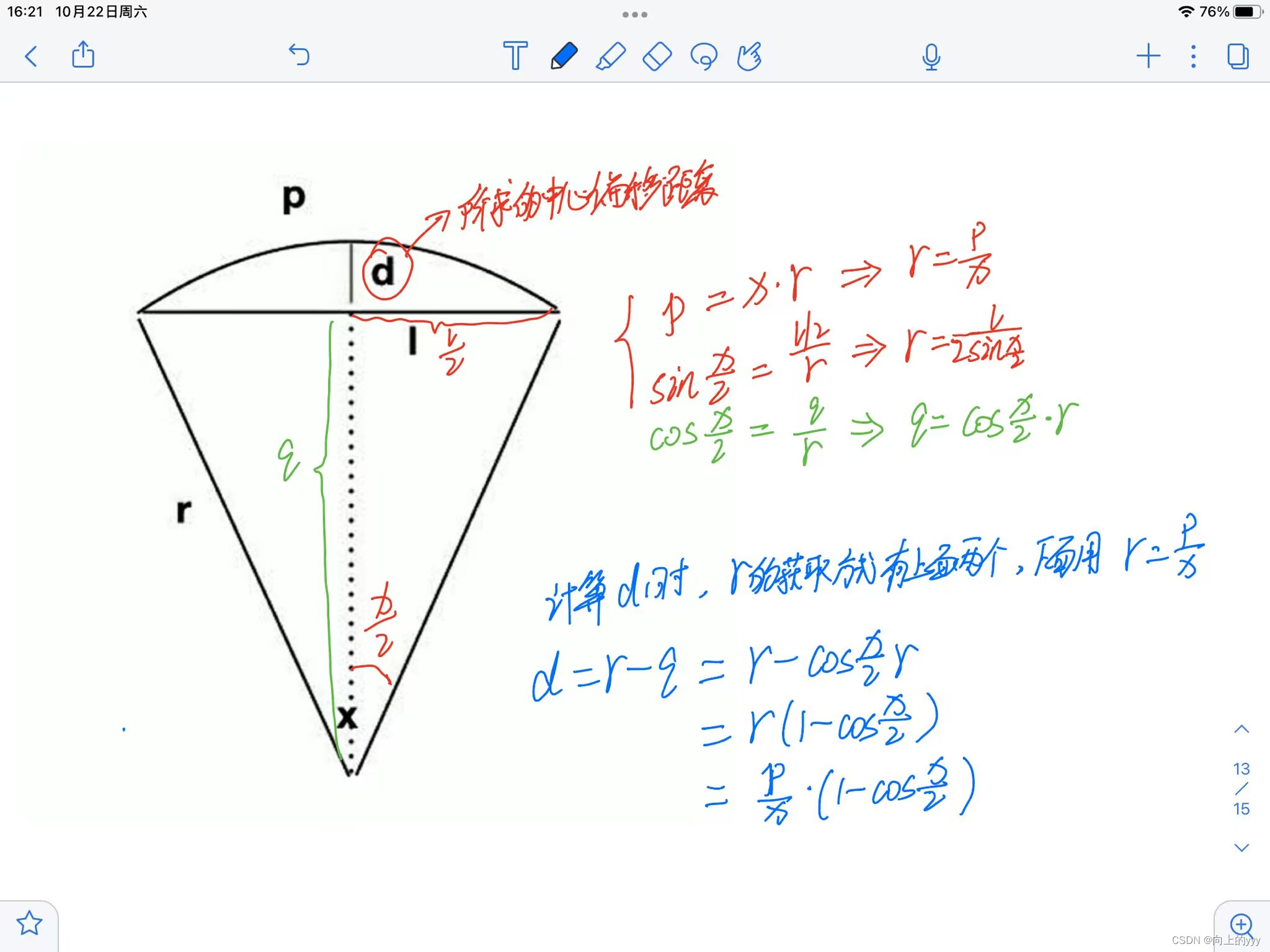
当一根细木棍被嵌在两堵墙之间被加热，它将膨胀形成弓形的弧，而这个弓形的弦恰好是未加热前木棍的原始位置。

你的任务是计算木棍中心的偏移距离。

【输入】
三个非负实数：木棍初始长度（单位：毫米），温度变化（单位：度），以及材料的热膨胀系数。

保证木棍不会膨胀到超过原始长度的1.5倍。

【输出】
木棍中心的偏移距离（单位：毫米），保留到小数点后第三位。

【输入样例】
1000 100 0.0001
【输出样例】
61.329

分析

1. 此题就是二分圆心角x，弧长等于x*r，圆心角x影响弧长的大小，通过枚举的圆心角，求得弧长与题目公式求得的弧长进行比较判断；
2. r的表示方式有两种，最后求d时用的r是用r=p/x，用这样表示r=l/(2sin(x/2))，会出现测试点过不去，可能是多次精度运算，精度丢失了；但是在枚举圆心角x求弧长时，r用的是l/(2sin(x/2))，因为这时候是求圆心角为x时弧长的pp，就不能用刚开始算好的弧长p来验证圆心角；
3. 还有就是二分时候while的条件，起初用的0.0001，因为答案说精确到三位，但有测试点wa了，然后试着多精确点，所以二分题部分测试点过不去，可以试着改 while条件的<= ，以及精度，以及l和r的取值；

#include<bits/stdc++.h>

using namespace std;
double l, n, c, p, d;
double PI = acos(-1);// π

//当圆心角为x时，所求的弧长
double calPP(double x) {
    double r = l / (2 * sin(x / 2));//半径
    double pp = r * x;//圆心角为x时的弧长
    return pp;
}

int main() {
    std::ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> l >> n >> c;
    p = (1 + n * c) * l;//弧长

    //枚举圆心角x，最小为0，最大为π
    double left = 0, right = PI, x;
    while (right - left >= 0.0000000001) {
        //圆心角x
        x = left + (right - left) / 2;
        //x下的弧长
        double pp = calPP(x);//pp = x*r
        //pp与题目公式求得的弧长p进行判断处理
        if (pp >= p) {
            //pp=x*r，pp大了说明x太大了
            right = x;
        } else {
            //x小了
            left = x;
        }
    }
    //d=p/x*(1-cos(x/2))  用r=p/x
    printf("%.3lf", p / x * (1 - cos(x / 2)));
    //d=(l/(2*sin(x/2)))*(1-cos(x/2)),用这样表示r=l/(2*sin(x/2))，会出现测试点过不去，可能是多次精度运算，精度丢失了
    //printf("%.3lf", (l / (2 * sin(x / 2))) * (1 - cos(x / 2)));
    return 0;
}