【2023考研数学二考试大纲】

I 考试科目

高等数学、线性代数

II考试形式和试卷结构

一、试卷满分及考试时间

试卷满分为150分，考试时间为180分钟

二、答题方式

答题方式为闭卷、笔试

三、试卷内容结构

高等教学 约80%
线性代数 约20%

四、试卷题型结构

单项选择题10小题，每小题5分，共50分
填空题6小题，每小题5分，共30分
解答题（包括证明题）6小题，共70分

III考查内容

【高等数学】

一、函数、极限、连续

【考试内容】

函数的概念及表示法
函数的有界性、单调性、周期性和奇偶性
复合函数、反函数、分段函数和隐函数
基本初等函数的性质及其图形
初等函数
函数关系的建立
数列极限与函数极限的定义及其性质
函数的左极限与右极限
无穷小量和无穷大量的概念及其关系
无穷小量的性质及无穷小量的比较
极限的四则运算
极限存在的两个准则：单调有界准则和夹逼准则
两个重要极限：

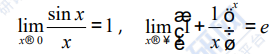
函数连续的概念
函数间断点的类型
初等函数的连续性
闭区间上连续函数的性质

【考试要求】

1. 理解函数的概念，掌握函数的表示法，并会建立应用问题的函数关系。
2. 了解函数的有界性、单调性、周期性和奇偶性。
3. 理解复合函数及分段函数的概念，了解反函数及隐函数的概念。
4. 掌握基本初等函数的性质及其图形，了解初等函数的概念。
5. 理解极限的概念，理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系。
6. 掌握极限的性质及四则运算法则。
7. 掌握极限存在的两个准则，并会利用它们求极限，掌握利用两个重要极限求极限的方法。
8. 理解无穷小量、无穷大量的概念，掌握无穷小量的比较方法，会用等价无穷小量求极限。
9. 理解函数连续性的概念（含左连续与右连续），会判别函数间断点的类型。
10. 了解连续函数的性质和初等函数的连续性，理解闭区间上连续函数的性质（有界性、最大值和最小值定理、介值定理），并会应用这些性质。

二、一元函数微分学

【考试内容】

导数和微分的概念
导数的几何意义和物理意义
函数的可导性与连续性之间的关系
平面曲线的切线和法线
导数和微分的四则