【写在前面:本专栏系列文章即为《算法设计与分析》学习过程中大实验的实验报告和实验代码,实验报告原文和源代码均已上传。有兴趣的小伙伴可以订阅专栏哦~】
目录
一、实验目的
1. 掌握分治法的基本思想
基本思想:即将一个规模为n的问题分解为k个规模为m的相互独立且与原问题解法相同的子问题,然后将子问题的解合并得到原问题的解。
2. 掌握相关问题的分治算法
(1) 第k小元素问题
(2) 大整数乘法问题
3. 验证、巩固和补充课堂讲授的理论知识。
二、实验内容
1. 第k小元素问题
从n个数中查找第k小元素
2.大整数乘法问题
采用分治法实现两个十进制大整数的乘法。
三、实验结果及分析
主要包括算法设计思路,详细设计、调试分析、运行结果以及算法的时间复杂度分析等。
1.算法设计
(1)第k小元素问题
使用快速排序中所采用的分划方法,以主元为基准,将一个表划分成左右两个子表,左子表中的所有元素均小于或等于主元,而右子表中的元素均大于或等于主元。设原表长度为n,假定经过一趟分划,分成两个左右子表,其中左子表是主元及其左边元素的子表,设其长度为p,右子表是主元右边元素的子表。那么,若k=p,则主元就是第k小元素;否则若k<p,第k小元素必定在左子表中,需求解的子问题成为在左子表中求第k小元素;若k>p,则第k小元素必定在右子表中,需求解的子问题成为在右子表中求第k-p小元素。
(2)大整数乘法问题
记X,Y是两个n为的十进制大整数。将X,Y根据位数截成两部分,即:
X=x1*10(n/2)+x0;Y=y1*10(n/2)+y0。
此时
X*Y=(x1*10(n/2)+x0)*(y1*10(n/2)+y0)=(x1*y1)*10(n/2)*2+(x1*y0)
2.思路分析
(1)第k小元素
Step 1选择选择一个元素(通常为第一个元素)作为标兵,然后通过两个指针进行遍历,遍历的方式如:i从左往右,j从右往左。当下标为i的元素值大于标兵时,i即停止移动;当下标为j的元素值小于标兵时,j即停止移动;然后调换i和j的元素位置。然后再重复上述步骤直到i>j停止。停止后调换标兵和j所指元素。第一遍结束。
Step 2第一遍结束之后,可以把标兵元素放在对应的位置上。
Step 3循环step1&step2直到标兵+1所在的位置即为第k小元素的位置。
(2)大整数乘法
Step 1将输入的两个大整数根据数位长度切分为四个大整数;
Step 2将得到的四个大整数根据计算公式调用计算函数进行计算,当输入到函数中的数字只有一位时计算返回;
Step 3逐层返回计算。
3.核心代码
(1)第K小元素
void Swap(int a,int b){
int tmp;
tmp=l[a];
l[a]=l[b];
l[b]=tmp;
}
int Partition(int left,int right){
while(left<=right){
int i=left,j=right+1;
do{
do i++; while(l[i]<l[left]);
do j--; while(l[j]>l[left]);
if(i<j) Swap(i,j);
}while(i<j);
Swap(left,j);
return j;
}
}
int Select(int k,int a,int b){
if(b<=0||k>b||k<=0) return -1;
int left=a,right=b,j;
l[b]=INFTY;
do{
j=rand()%(right-left+1)+left;
Swap(left,j);
j=Partition(left,right);
if(k==j+1) return l[j];
else if(k<j+1) right=j;
else left=j+1;
}while(left<=right);
}(2)大整数乘法
long long mutipy(long long a,long long b,int num){
int s;
if((a>0&&b>0)||(a<0&&b<0)) s=1;
else s=-1;
a=(a>0)?a:-a ;
b=(b>0)?b:-b ;
if(num==0) return 0;
else if(num==1){
return s*a*b;
}
else{
long long A=a/(int)pow(10,(int)(num/2));
long long B=a%(int)pow(10,(int)(num/2));
long long C=b/(int)pow(10,(int)(num/2));
long long D=b%(int)pow(10,(int)(num/2));
long long AC=mutipy(A,C,(int)(num/2));
long long BD=mutipy(B,D,(int)(num/2));
long long ABCD=mutipy((A-B),(D-C),(int)(num/2))+AC+BD;
return s*(long long)(AC*pow(10,(int)(num/2)+(int)(num/2))+ABCD*pow(10,(int)(num/2))+BD);
}
}4.测试样例设计
(1)第k小元素问题
测试样例1
| 输入 | 6 5 2 9 12 8 10 3 |
| 输出 | 8 |
测试样例2
| 输入 | 8 4 2 9 1 6 7 3 10 3 |
| 输出 | 3 |
(2)大整数乘法
测试样例1
| 输入 | 9486543 47698536 |
| 输出 | 452494212801048 |
测试样例2
| 输入 | 456123 456987 |
| 输出 | 208442281401 |
5.运行结果(截图)
(1)第k小元素
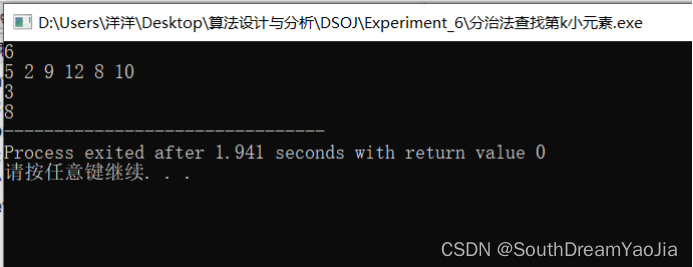

(2)大整数乘法
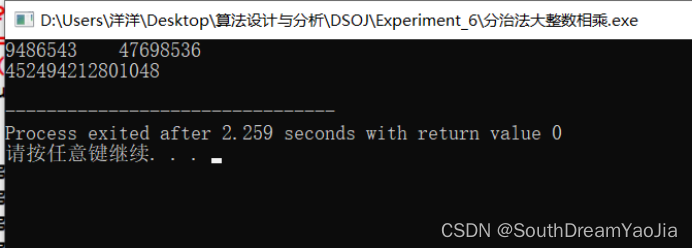
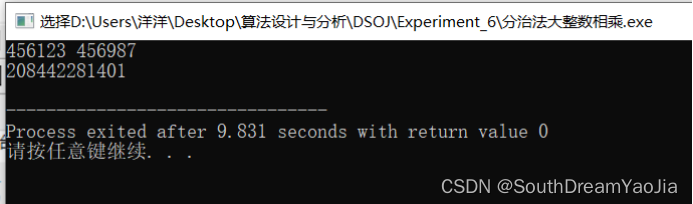
6.难点分析
(1)Point1
Partion函数实现:置换i和j的值发生错误。
Partion函数和Swap函数中经常需要更改数组的值,因此使用全局数组以减少数组的传递。
(2)Point2
大整数切分完之后返回值的处理不清楚。
7.算法时间复杂度分析
(1)第k小元素
Partition()函数中以i和j遍历每个元素,时间复杂度为O(n)。
Select()函数时间复杂度为O(n)。
(2)大整数乘法
mutipy()函数时间复杂度为:
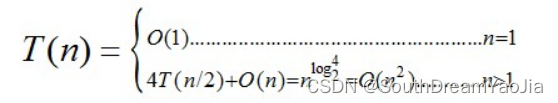
四、总结
通过此次的实验,对分治法的算法思想有了更深的了解,也就是把一个复杂的问题分成两个或多个相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。同时,因为需要分解原问题并合并子问题的解,因此需要使用递归的方式进行分解与合并。因此在熟练运用分治法之前更应该要熟练掌握递归的知识。
























 3137
3137











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










