信息论与编码2 期末复习-线性码

线性码

定义

如果C∈V(n,q)是V(n,q)的一个子空间,则称C为一个q元线性码.如果C是V(n,q)的一个k维子空间,则称C为一个q元[n,k] 线性码.进一步,如果C的最小距离是d,则称C为一个q元[n,k,d]线性码.

例：

对任意一个线性码C,零向量都为其一个码字.
q元[n, k,d]线性码自然是一个q元(n,qk,d)码. 但反过来不一定成立
例：

线性码的一个非常重要的性质是它的最小距离与最小重量相等.
设C是一个码字,则d( C)=W( C).

生成矩阵

设C是一个q元[n,k|线性码。将C的一组基作为行向量构成一个k x n矩阵G。G称为线性码C的生成矩阵.

例如：

一个线性码C的生成矩阵的行向量的任意线性组合都是C的码字。反过来,C的任意一个码字也都可以表示为生成矩阵G的行向量的一个线性组合。
由于线性码C的基不是唯一一的，所以线性码C的生成矩阵也不唯一.

标准生成矩阵(码的等价)

码的变换：
设G1和G2是GF(g)上 的两个k x n矩阵，并且Rank(G1) = Rangk(G2)= k。如果可以通过一系列下述变换将G1变换成G2，则G1和G2生成的q元[n,k]线性码一定是等价的。

• (R1)重新排列行向量
• (R2)将某一行乘以一个非零元素
• (R3)将某一行乘以一个非零元素，然后加到另一行
• (C1)重新排列列向量
• (C2)将某一列乘以一个非零元素

标准生成矩阵：
设G是一个q元[n, k]线性码的生成矩阵。则通过一系列(R1)(R2)(R3)(C1)(C2)类型的变换，一定可以将G变换成型如($I_k$| A)的矩阵，其中$I_k$是一个k x k阶单位矩阵。A是一个k x (n- k)阶矩阵。
型如($I_k$| A)的生成矩阵为标准型生成矩阵。
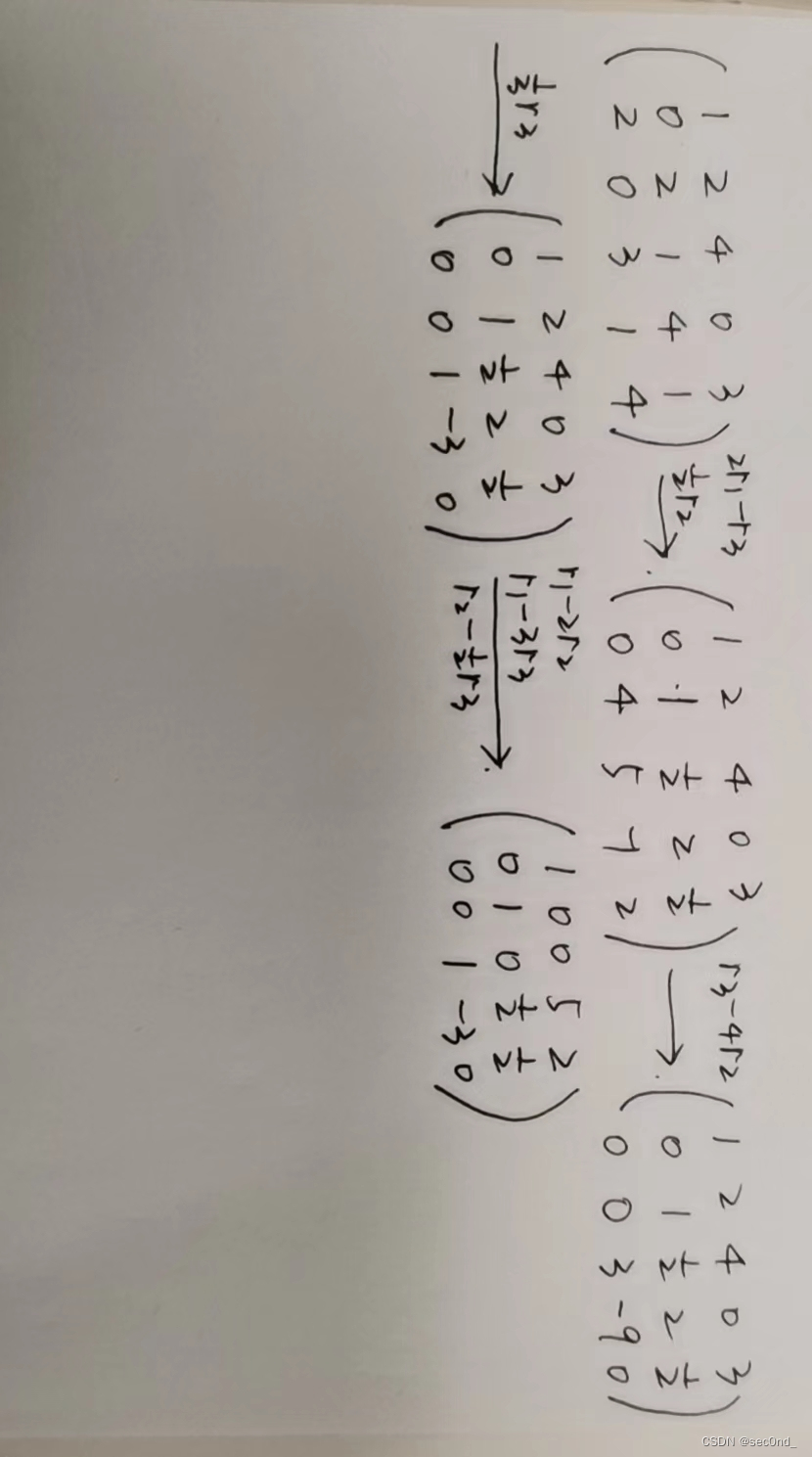
例如：（这个题我也变不对，找了位数学专业的同学帮忙变的，还差一步将列变成整数，乘以分母的最小公倍数即可）

编码

设C是一个q元[n,k]线性码，G为生成矩阵.C中的每个码字都是G的行向量的线性组合，即C= {uG|u∈V(k, q)}.

在这里补充下矩阵的乘法：

标准阵译码

例如：

信息位(K)有两位，m=00，01，10，11，许用码字为信息组m乘以生成矩阵G，C=00000，01101，10111，11010
也可以通过生成矩阵G，每行即是一个码字，相加也为码字，零码字也为码字

伴随式有2^(n-k) =2³=8个，所以标准阵有8行。

校验矩阵

对于一个q元[n,k]线性码C，如果生成矩阵为标准型G=($I_k$|A),则其校验矩阵为
H=(-A^T|$I_{(}n-k)$).
例：

伴随式译码

设C是一个q元[n,k]线性码，其校验矩阵为H。对任意y∈V(n,q)，称yH^T为y的伴随。记为s(y)。

伴随式译码方法：
一个q元[n,k]线性码C的伴随式译码方法描述如下:

1. 设y是在信道接收端收到的向量,计算y的伴随式S(y)
2. 在伴随式列表中找到S(y)所对应的陪集元代表a
3. 将y译为码字y-a