目录
投资案例
模型假设:
①每种投资是否收益是相互独立的
②在短时期内所购买的各种资产(如股票,证券等)不进行买卖交易,即在买入后就不再卖出
③在投资的过程中,无论盈利与否必须先付交易费
④在短时期内所给出的平均收益率、损失率和交易的费率不变
单目标线性规划:
其中r表示平均收益率,q表示风险损失率,p为交易费费率,x为投资金额。
clear all
clc
f=-[0.05,0.075,0.153,0.434,0.224,0.005,0.106,0.351,...
0.281,0.309,0.339,0.067,0.033,0.323,0.049,0.074]'; %目标向量
A=zeros(15,15);
a=[0.42,0.54,0.6,0.42,0.012,0.39,0.68,0.3343,0.533,0.4,0.31,0.055,0.46,0.053,0.23];
B=diag(a,0);
a=zeros(15,1);
A=[a,B]; %不等式左端的系数矩阵
aeq=[1,1.021,1.032,1.06,1.015,1.076,1.034,1.056,1.031,...
1.027,1.029,1.051,1.057,1.027,1.045,1.076];
beq=[1];
lb=zeros(16,1);
i=1;
for k=0.01:0.04:0.62
b=[k,k,k,k,k,k,k,k,k,k,k,k,k,k,k]';
[x,fval,exitflag,options,output]=linprog(f,A,b,aeq,beq,lb);
x
y(i)=-fval
i=i+1;
end
k=0.01:0.04:0.62;
plot(k,y);
xlabel('风险');
ylabel('收益');
title('风险收益图(n=15)') 
销售案例
clear all clc c=[-10 -9]; A=[6 5;10 20;1 0]; b=[50;160;8]; Aeq=[]; beq=[]; vlb=[0;0]; vub=[]; [x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub) 结果: x = 2.8571 6.5714 fval = -87.7143








 文章展示了使用线性规划方法解决投资和销售问题的实例。在投资案例中,探讨了基于平均收益率、风险损失率和交易费用的单目标线性规划,通过调整风险参数生成风险收益图。在销售案例中,优化了产品组合以最大化利润。
文章展示了使用线性规划方法解决投资和销售问题的实例。在投资案例中,探讨了基于平均收益率、风险损失率和交易费用的单目标线性规划,通过调整风险参数生成风险收益图。在销售案例中,优化了产品组合以最大化利润。
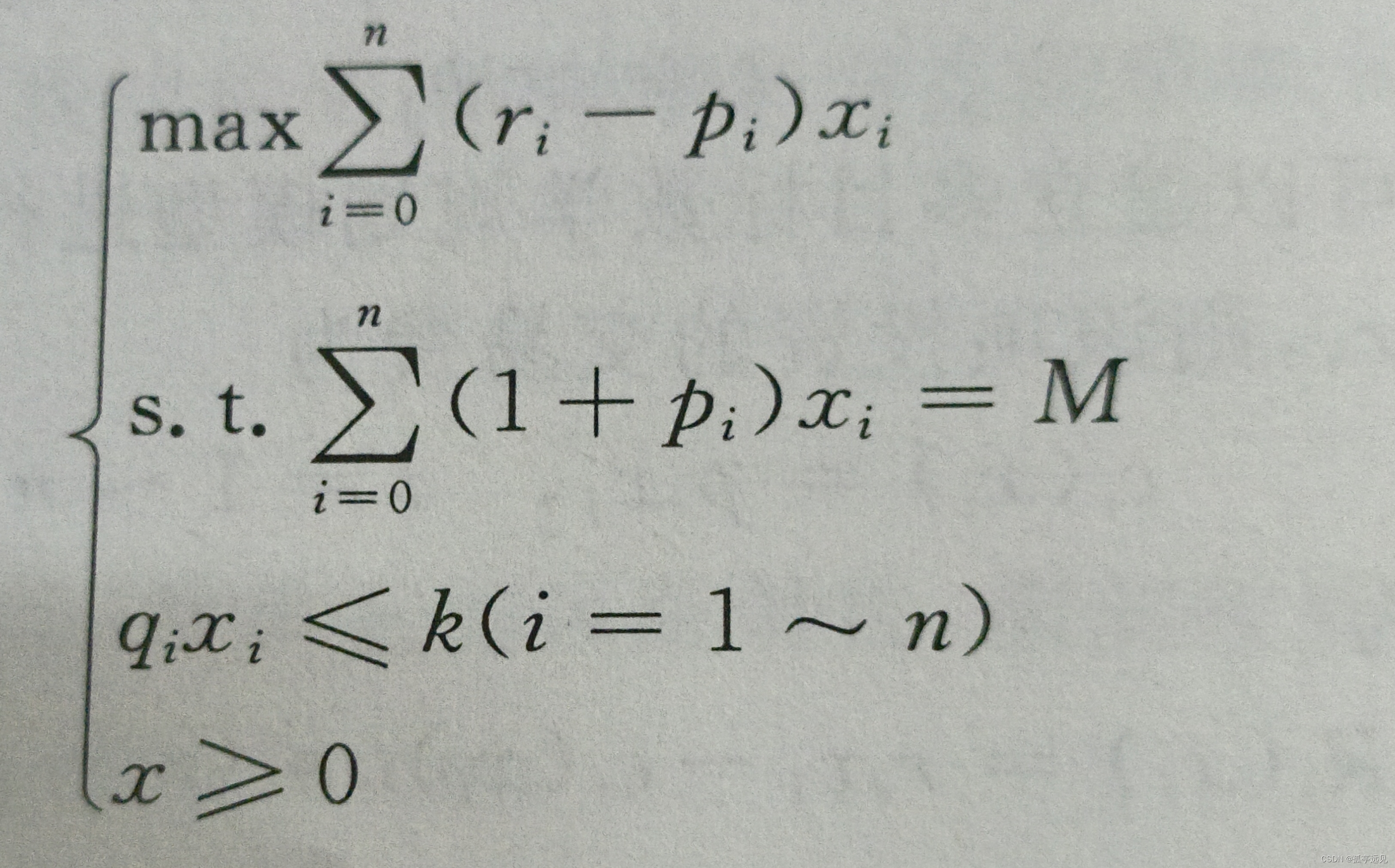
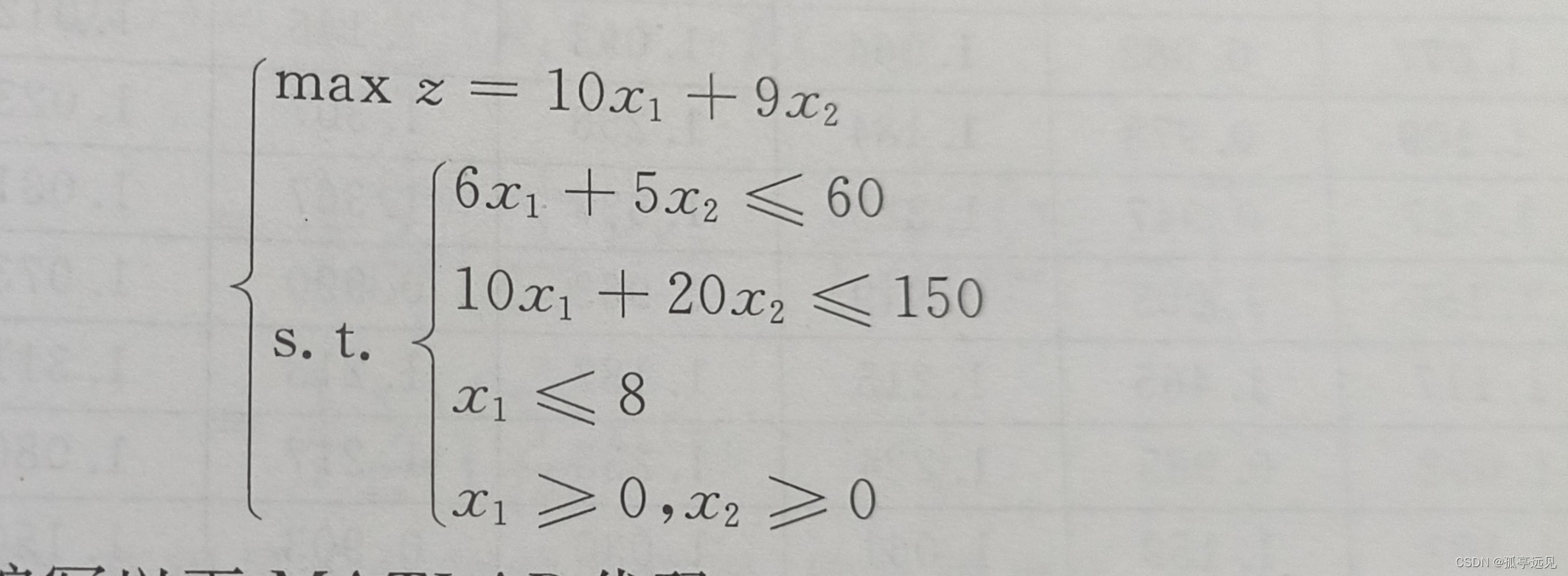

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








