集成学习与强化学习：Bagging, Boosting, GBDT及其应用-CSDN博客

本文链接：https://blog.csdn.net/weixin_52733693/article/details/127866409

5.1 集成学习算法简介

学习目标

了解什么是集成学习
了解集成学习中的boosting和bagging

1 什么是集成学习

某投资方想投资一家公司A，但他还不知道它的业绩。所以他想有人给他提意见，看看这家公司的股票价格是否每年增长6%以上。

集成学习通过建立几个模型来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自作出预测。这些预测最后结合成组合预测，因此优于任何一个单分类的做出预测。

2 生活中的集成学习

1.买东西找别人推荐

2.唱歌比赛投票

每个人的视角不同、经历不同、给出的决策背后的原因不同

3 复习：机器学习的两个核心任务

任务一：如何优化训练数据 —> 主要用于解决欠拟合问题
任务二：如何提升泛化性能 —> 主要用于解决过拟合问题

4 集成学习中boosting和Bagging

**Bagging中每个训练集互不相关，也就是每个基分类器互不相关，而Boosting中训练集要在上一轮的结果上进行调整，也使得其不能并行计算

**
Bagging中预测函数是均匀平等的，但在Boosting中预测函数是加权的

从算法来看，Bagging关注的是多个基模型的投票组合，每一个基模型相对复杂一些，Bagging可以降低方差；而Boosting采用的策略是在每一次学习中都减少上一轮的偏差。

5 小结

什么是集成学习【了解】
- 通过建立几个模型来解决单一预测问题
机器学习两个核心任务【知道】
- 1.解决欠拟合问题
  - 弱弱组合变强
  - boosting
- 2.解决过拟合问题
  - 互相遏制变壮
  - Bagging

5.2 Bagging和随机森林

学习目标

知道Bagging集成原理
知道随机森林构造过程
知道什么是包外估计
知道RandomForestClassifier的使用
了解bagging集成的优点

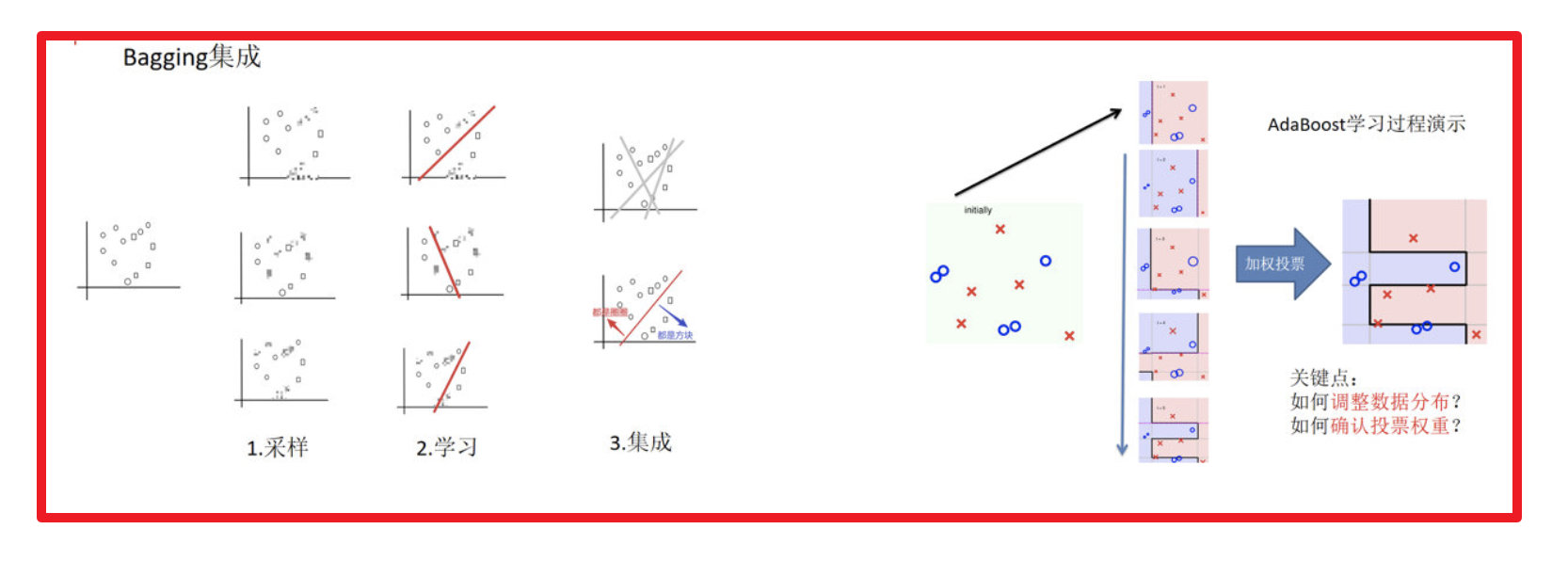
1 Bagging集成原理

Bagging

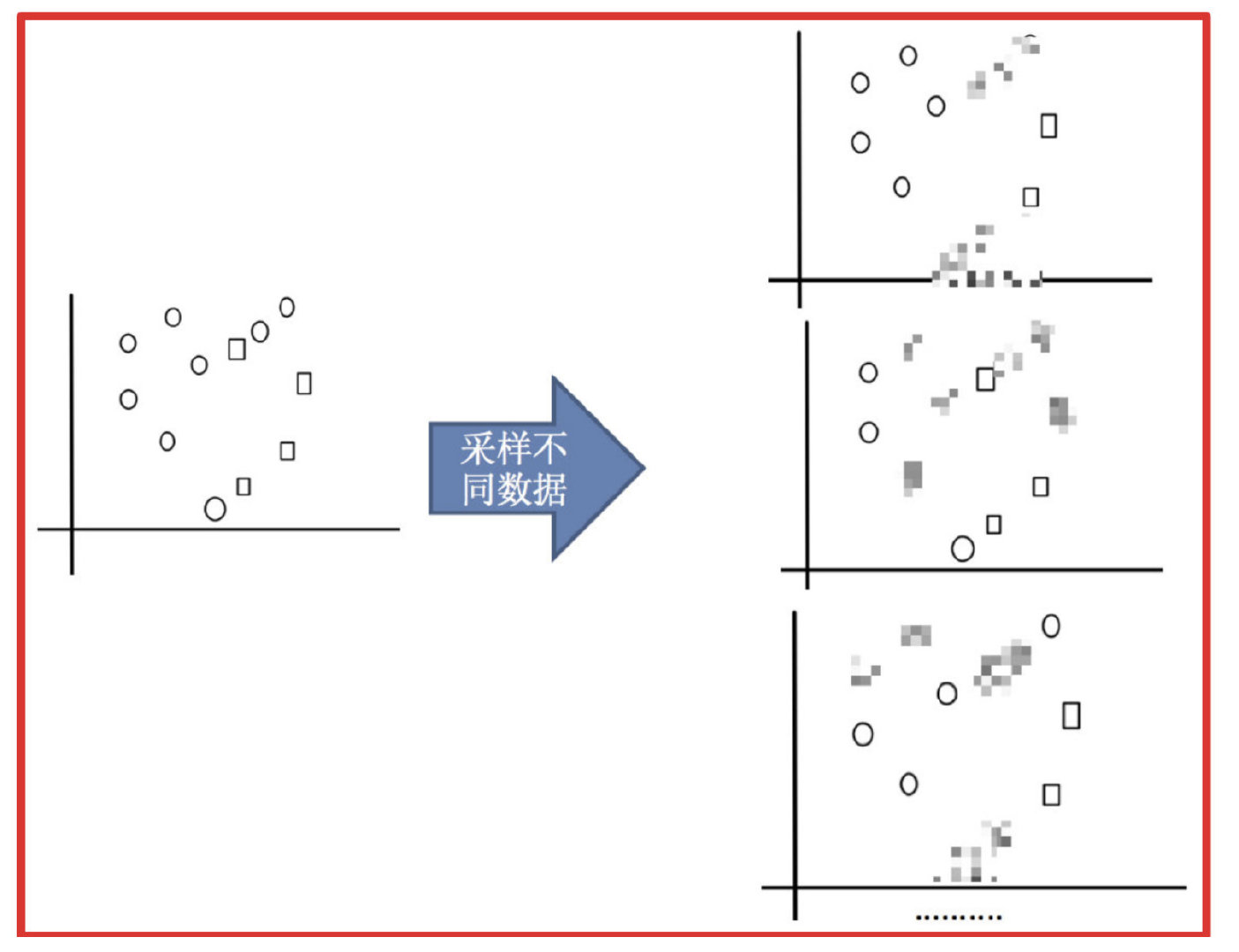
Bagging是bootstrap aggregating的简写。先说一下bootstrap，bootstrap也称为自助法，它是一种有放回的抽样方法。

在Bagging方法中，利用bootstrap方法从整体数据集中采取有放回抽样得到N个数据集，在每个数据集上学习出一个模型，最后的预测结果利用N个模型的输出得到，具体地：分类问题采用N个模型预测投票的方式，回归问题采用N个模型预测平均的方式。

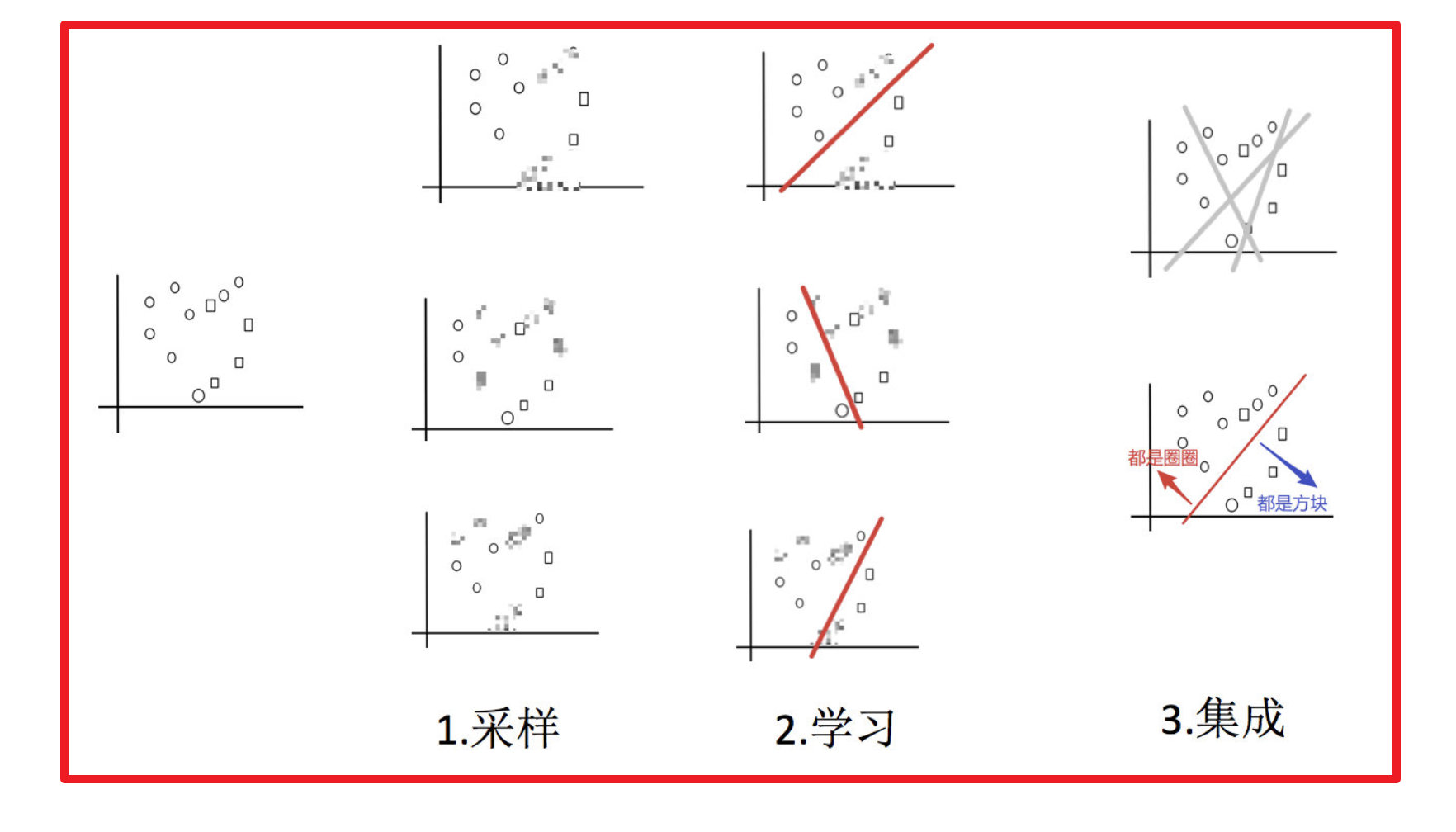
例：

目标：把下面的圈和方块进行分类

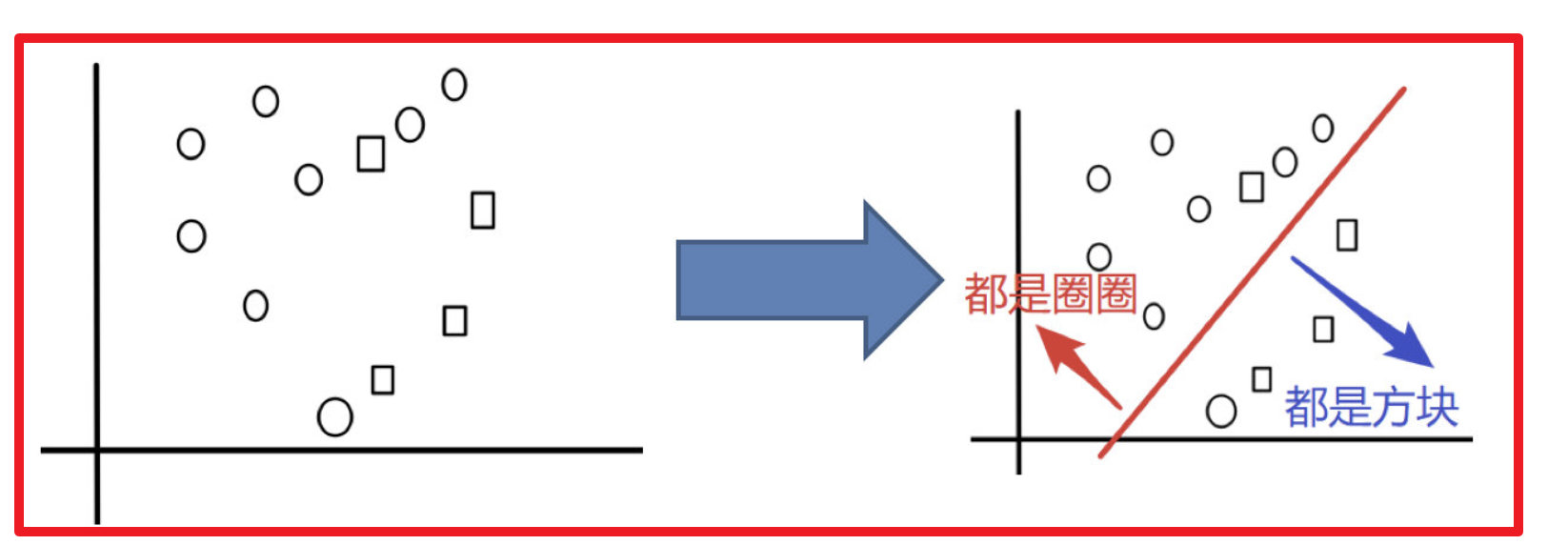
实现过程：

采样不同数据集

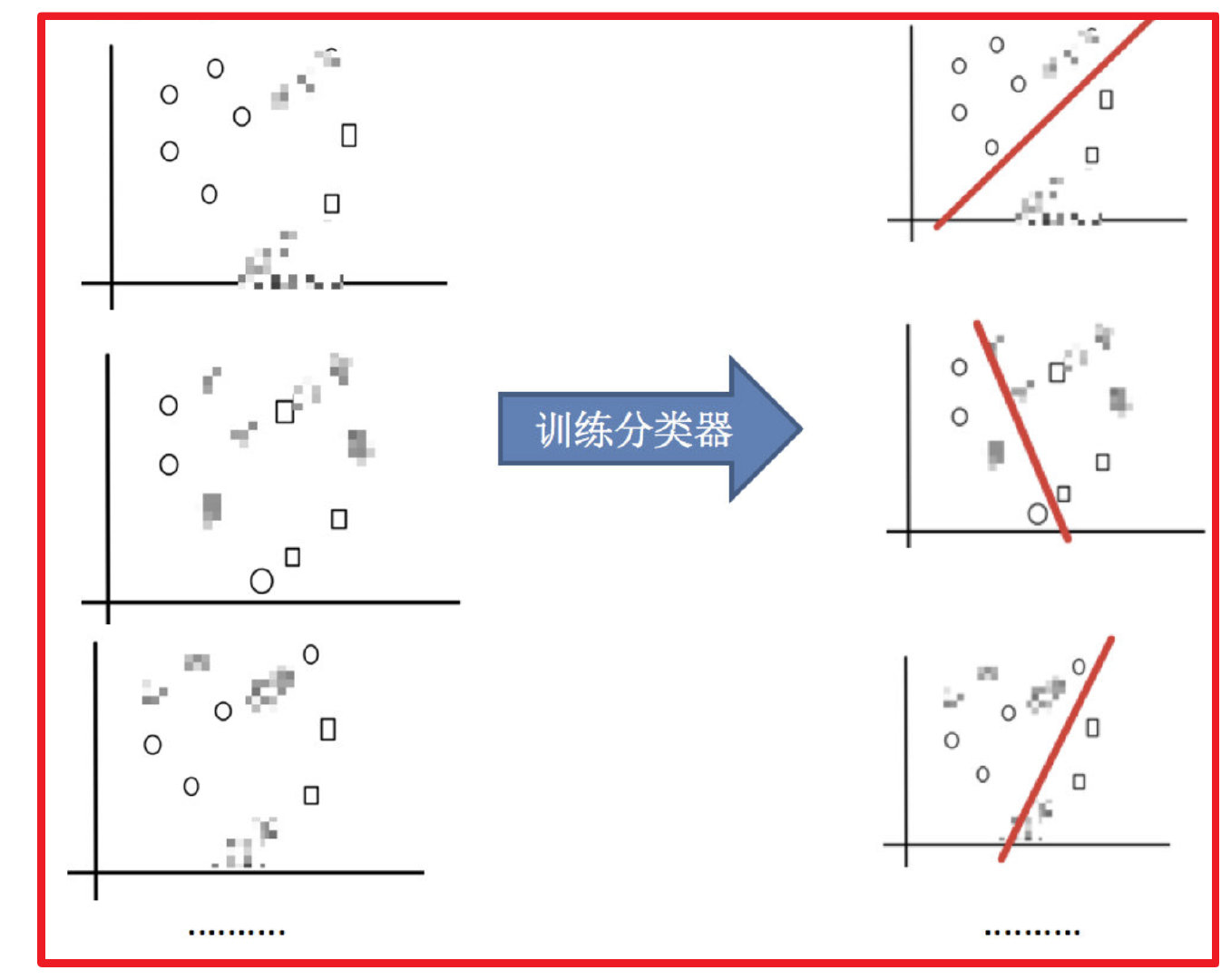
2)训练分类器

3)平权投票，获取最终结果

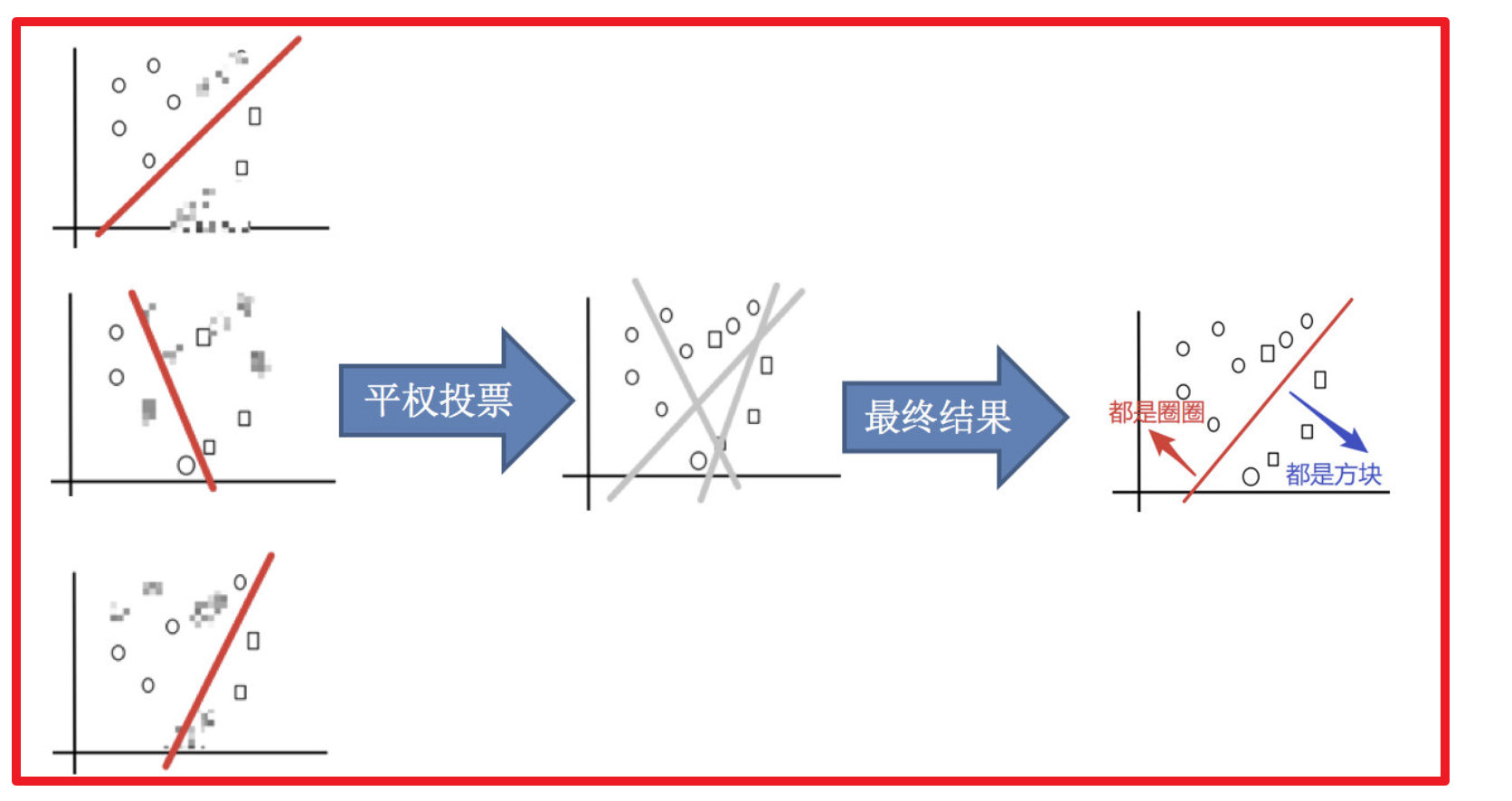
4)主要实现过程小结

2 bagging经典算法：随机森林

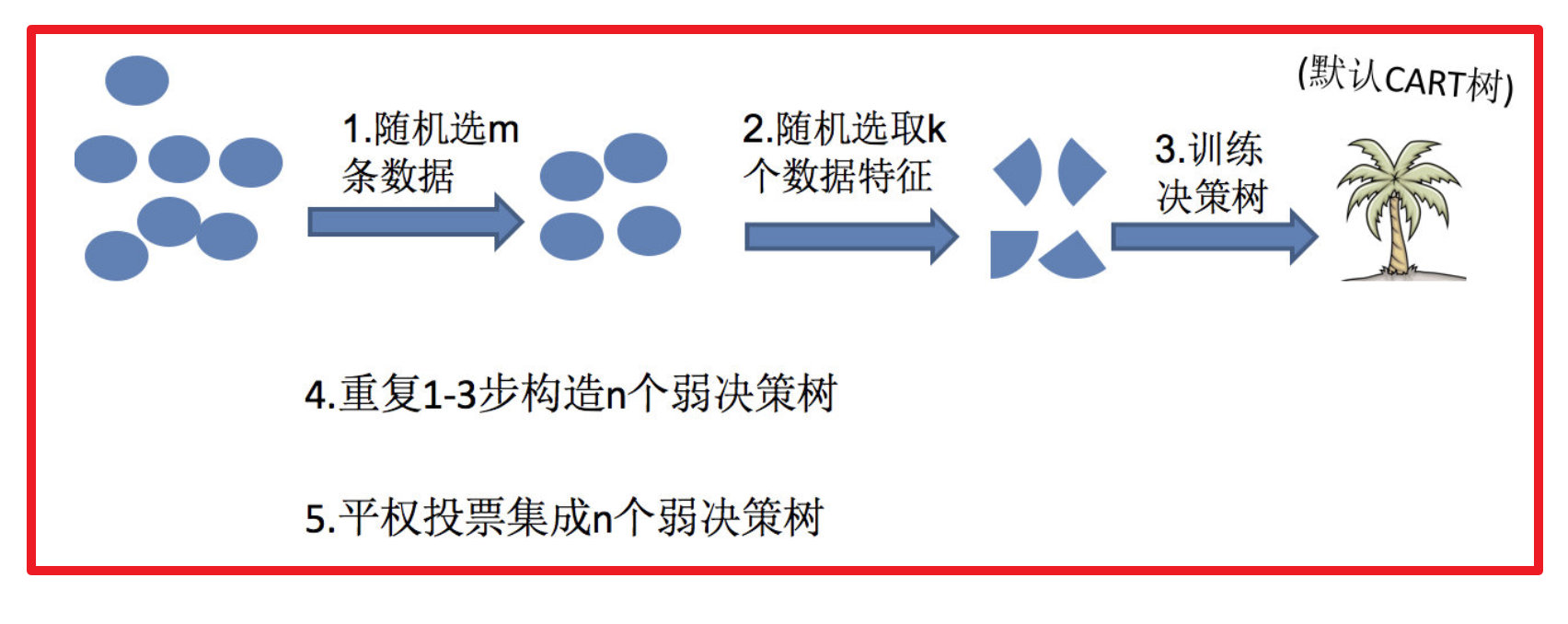
在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

随机森林 = Bagging + 决策树

例如, 如果你训练了5个树, 其中有4个树的结果是True, 1个树的结果是False, 那么最终投票结果就是True

随机森林够造过程中的关键步骤(M表示特征数目)：

1)假设训练集总共有N个样本，一次随机选出一个样本，有放回的抽样，重复N次(会出现重复的样本)

2) 随机去选出m个特征, m <<M，建立决策树

（这两种方式都是为了使用相同的数据可以产生不同的决策树）

3 包外估计 (Out-of-Bag Estimate)

在随机森林构造过程中，如果进行有放回的抽样，我们会发现，总是有一部分样本我们选不到。

这部分数据，占整体数据的比重有多大呢？
这部分数据有什么用呢？

3.1 包外估计的定义

没有选择到的数据，称之为 Out-of-bag(OOB)数据，当数据足够多，包外数据的概率为：

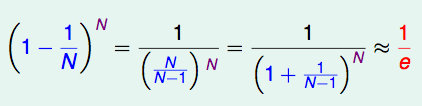
N为样本个数，1/N为样本选到的概率，

由于基分类器是构建在训练样本的自助抽样集上的，只有约 63.2％原样本集出现在中，而剩余的 36.8％的数据作为包外数据，可以用于基分类器的验证集。

经验证，包外估计是对集成分类器泛化误差的无偏估计.

oob_score
对于单棵用采样集训练完成的决策树Ti，用袋外数据运行后会产生一个oob_score ，对每一棵决策树都重复上述操作，最终会得到T个oob_score，把这T和oob_score平均，最终得到的就是整个随机森林的oob_score

3 随机森林api介绍

sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)
- n_estimators：integer，optional(default = 10)森林里的树木数量120,200,300,500,800,1200
  - 在利用最大投票数或平均值来预测之前，你想要建立子树的数量。
- Criterion：string，可选(default =“gini”)
  - 分割特征的测量方法
- max_depth：integer或None，可选(默认=无)
  - 树的最大深度 5,8,15,25,30
- max_features="auto”,每个决策树的最大特征数量
  - If “auto”, then max_features=sqrt(n_features).
  - If “sqrt”, then max_features=sqrt(n_features)(same as “auto”).
  - If “log2”, then max_features=log2(n_features).
  - If None, then max_features=n_features.
- bootstrap：boolean，optional(default = True)
  - 是否在构建树时使用放回抽样
- min_samples_split 内部节点再划分所需最小样本数
  - 这个值限制了子树继续划分的条件，如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分，默认是2。
  - 如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。
- min_samples_leaf 叶子节点的最小样本数
  - 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝，默认是1。
  - 叶是决策树的末端节点。较小的叶子使模型更容易捕捉训练数据中的噪声。
  - 一般来说，我更偏向于将最小叶子节点数目设置为大于50。
- min_impurity_split: 节点划分最小不纯度
  - 这个值限制了决策树的增长，如果某节点的不纯度(基于基尼系数，均方差)小于这个阈值，则该节点不再生成子节点。即为叶子节点。
  - 一般不推荐改动默认值1e-7。
上面决策树参数中最重要的包括
- 最大特征数max_features，
- 最大深度max_depth，
- 内部节点再划分所需最小样本数min_samples_split
- 叶子节点最少样本数min_samples_leaf。

4 随机森林预测案例

实例化随机森林

# 随机森林去进行预测
rf = RandomForestClassifier()

定义超参数的选择列表

param = {
   "n_estimators": [120,200,300,500,800,1200], "max_depth": [5, 8, 15, 25, 30]}

使用GridSearchCV进行网格搜索

# 超参数调优
gc = GridSearchCV(rf, param_grid=param, cv=2)

gc.fit(x_train, y_train)

print("随机森林预测的准确率为：", gc.score(x_test, y_test))

注意

随机森林的建立过程

树的深度、树的个数等需要进行超参数调优

所有代码

import pandas as pd
import numpy as np
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier


# 1、获取数据
titan = pd.read_csv("./data/titanic.txt")
#2.数据基本处理
#2.1 确定特征值,目标值
x = titan[["pclass", "age", "sex"]]
y = titan["survived"]
#2.2 缺失值处理
x['age'].fillna(x['age'].mean(), inplace=True)
#2.3 数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
#3.特征工程(字典特征抽取)
# 对于x转换成字典数据x.to_dict(orient="records")，orient:指定把dataframe的数据转换成什么格式
# records格式：[{"pclass": "1st", "age": 29.00, "sex": "female"}, {}]

transfer = DictVectorizer(sparse=False)

x_train = transfer.fit_transform(x_train.to_dict(orient="records"))
x_test = transfer.transform(x_test.to_dict(orient="records"))


# 4.机器学习(随机森林)
# 4.1实例化随机森林
rf = RandomForestClassifier()
#dt = DecisionTreeClassifier()
# 4.2 定义超参数的选择列表
param = {"n_estimators": [60,80,100,120], "max_depth": [3,5,7]}
#param = { "max_depth": [3,5,7]}
# 4.3 使用GridSearchCV进行网格搜索
from sklearn.model_selection import GridSearchCV
gc = GridSearchCV(rf, param_grid=param, cv=5)
#gc = GridSearchCV(dt, param_grid=param, cv=5)
# 4.4模型训练
gc.fit(x_train, y_train)
# 5.模型评估

print("随机森林预测的准确率为：", gc.score(x_test, y_test))

5 bagging集成优点

Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging集成学习方法

最常用的方法是 Bagging + 决策树，即随机森林。

经过上面方式组成的集成学习方法:

提高泛化正确率
简单, 方便, 通用

6 小结

bagging集成过程【知道】
- 1.采样 — 从所有样本里面，采样一部分
- 2.学习 — 训练弱学习器
- 3.集成 — 使用平权投票
随机森林介绍【知道】
- 随机森林定义
  - 随机森林 = Bagging + 决策树
- 流程：
  - 1.随机选取m条数据
  - 2.随机选取k个特征
  - 3.训练决策树
  - 4.重复1-3
  - 5.对上面的若决策树进行平权投票
- 注意：
  - 1.随机选取样本，且是有放回的抽取
  - 2.选取特征的时候吗，选择m<<M
  - M是所有的特征数
- 包外估计
  - 如果进行有放回的对数据集抽样，会发现，总是有一部分样本选不到；
- api
  - sklearn.ensemble.RandomForestClassifier()
Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging集成学习方法【了解】
bagging的优点【了解】
- 1.均可在原有算法上提高约2%左右的泛化正确率
- 2.简单, 方便, 通用

5.3 otto案例介绍 – Otto Group Product Classification Challenge

1.背景介绍

奥托集团是世界上最大的电子商务公司之一，在20多个国家设有子公司。该公司每天都在世界各地销售数百万种产品,所以对其产品根据性能合理的分类非常重要。

不过,在实际工作中,工作人员发现,许多相同的产品得到了不同的分类。本案例要求,你对奥拓集团的产品进行正确的分类。尽可能的提供分类的准确性。

链接：https://www.kaggle.com/c/otto-group-product-classification-challenge/overview

2nd iteration

2.数据集介绍

本案例中，数据集包含大约200,000种产品的93个特征。
其目的是建立一个能够区分otto公司主要产品类别的预测模型。
所有产品共被分成九个类别（例如时装，电子产品等）。

id - 产品id
feat_1, feat_2, …, feat_93 - 产品的各个特征
target - 产品被划分的类别

3.评分标准

本案例中，最后结果使用多分类对数损失进行评估。

具体公式：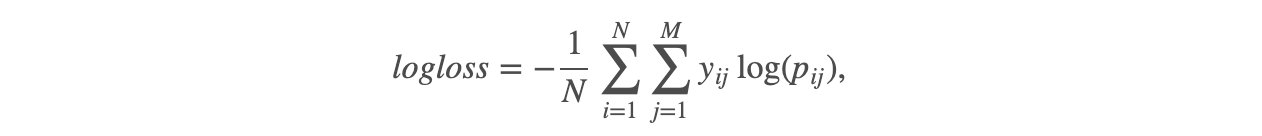

上公式中，

i表示样本，j表示类别。Pij代表第i个样本属于类别j的概率，
如果第i个样本真的属于类别j，则yij等于1，否则为0。
根据上公式，假如你将所有的测试样本都正确分类，所有pij都是1，那每个log(pij)都是0，最终的logloss也是0。
假如第1个样本本来是属于1类别的，但是你给它的类别概率pij=0.1，那logloss就会累加上log(0.1)这一项。我们知道这一项是负数，而且pij越小，负得越多，如果pij=0，将是无穷。这会导致这种情况：你分错了一个，logloss就是无穷。这当然不合理，为了避免这一情况，我们对非常小的值做如下处理：

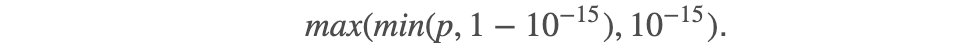
也就是说最小不会小于10^-15。

5.4 Boosting

学习目标

知道boosting集成原理和实现过程
知道bagging和boosting集成的区别
知道AdaBoost集成原理

1 什么是boosting

随着学习的积累从弱到强

简而言之：每新加入一个弱学习器，整体能力就会得到提升

代表算法：Adaboost，GBDT

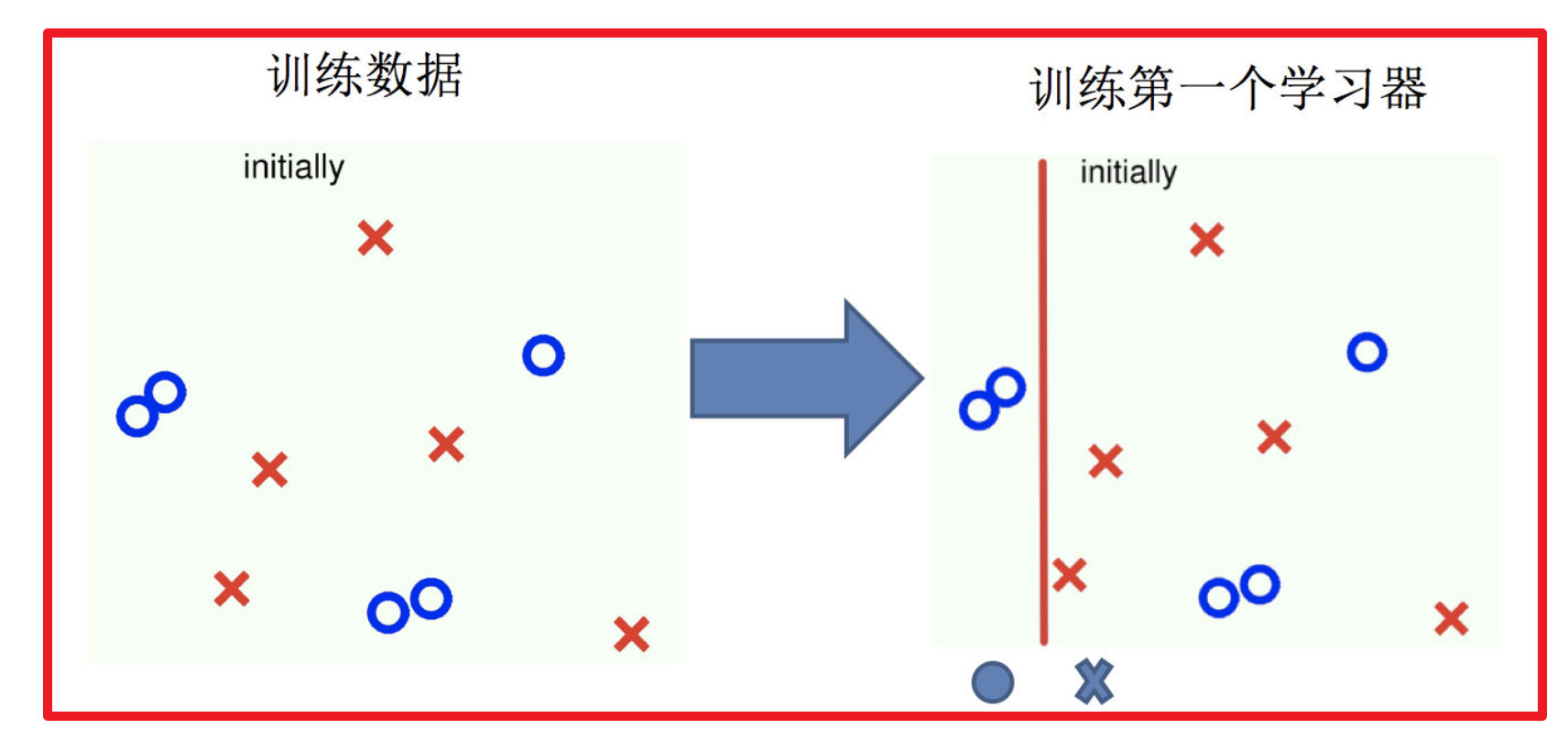
2 实现过程：

1.训练第一个学习器

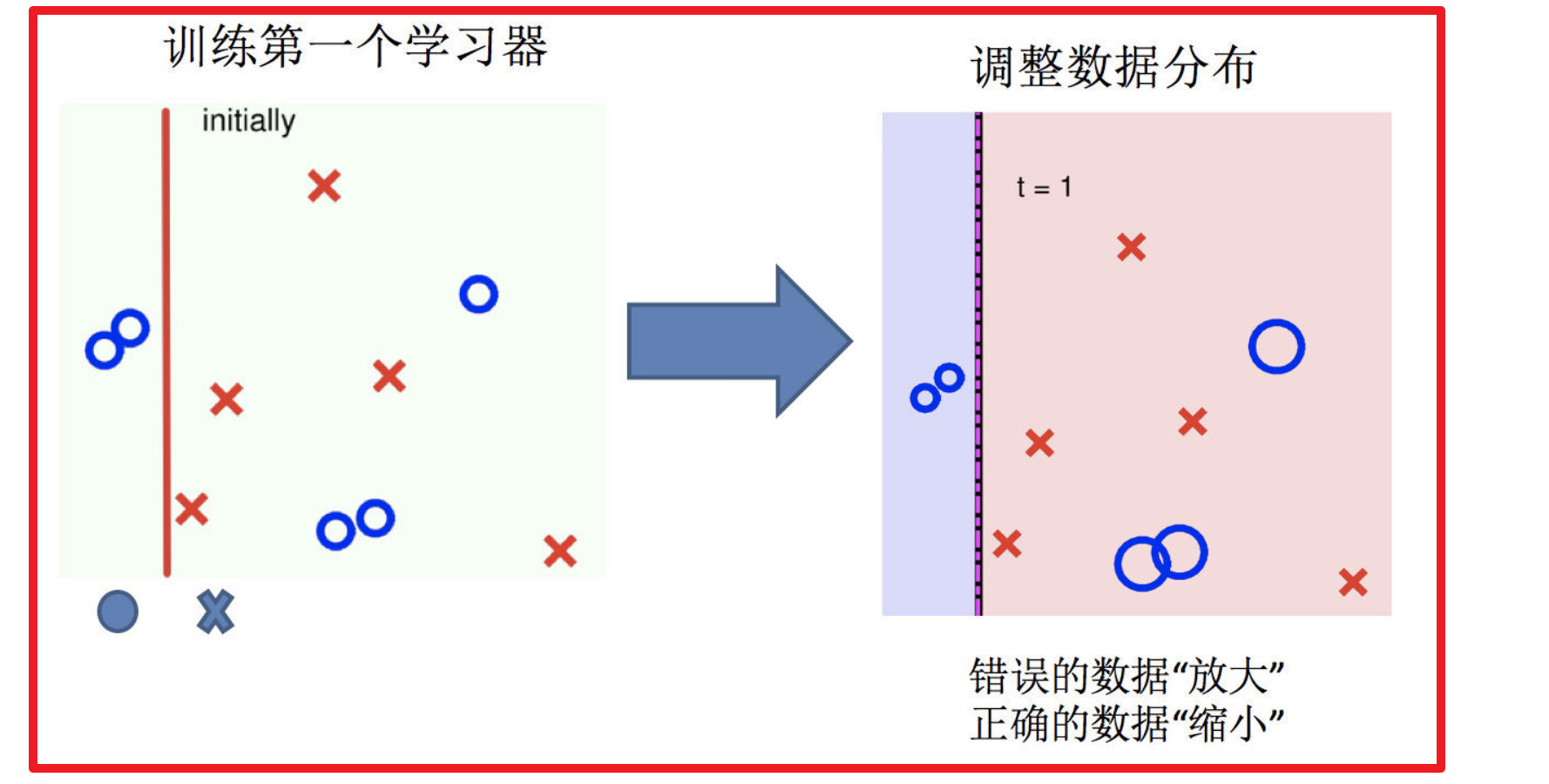
2.调整数据分布

3.训练第二个学习器

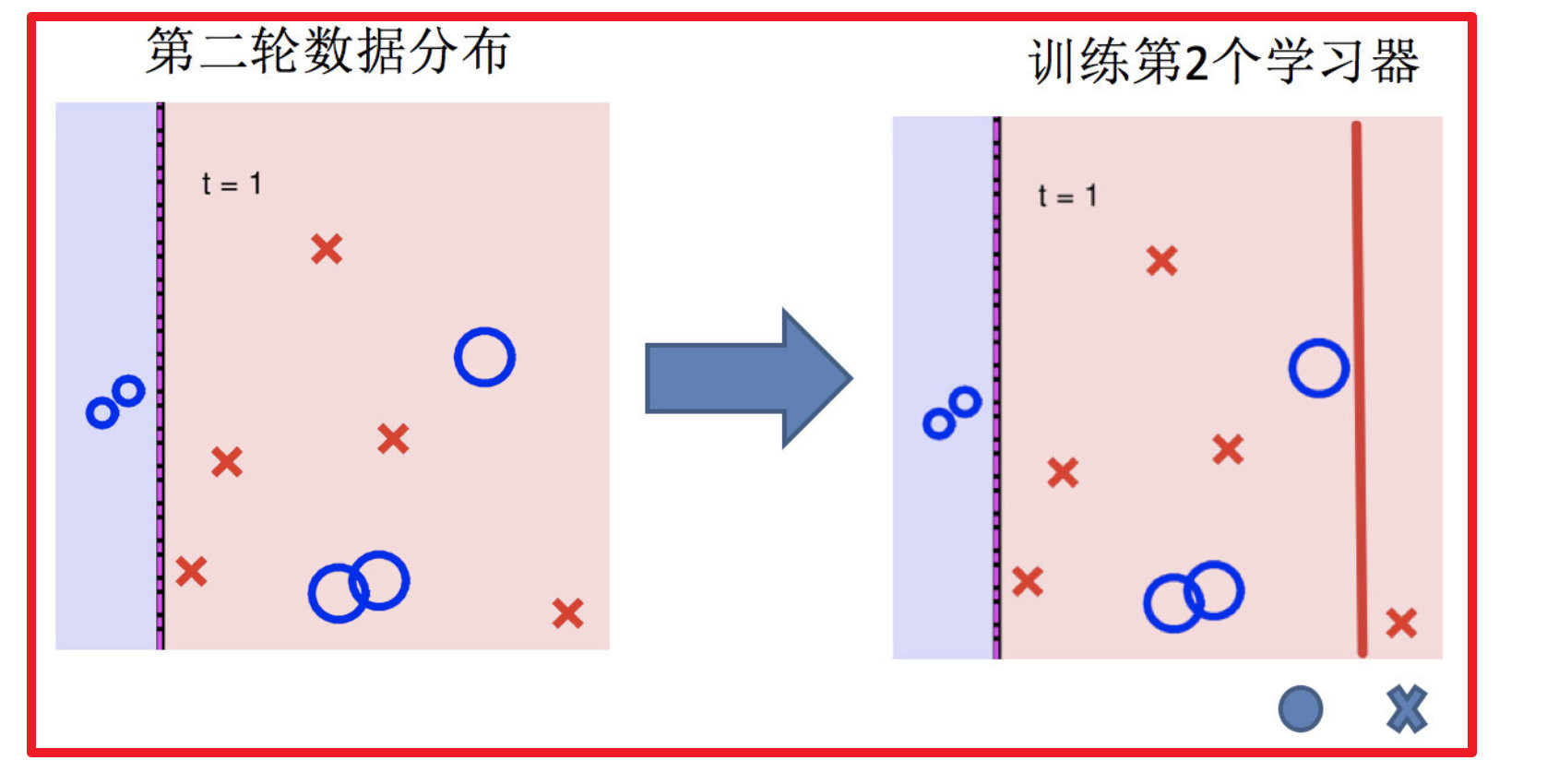
4.再次调整数据分布

5.依次训练学习器，调整数据分布

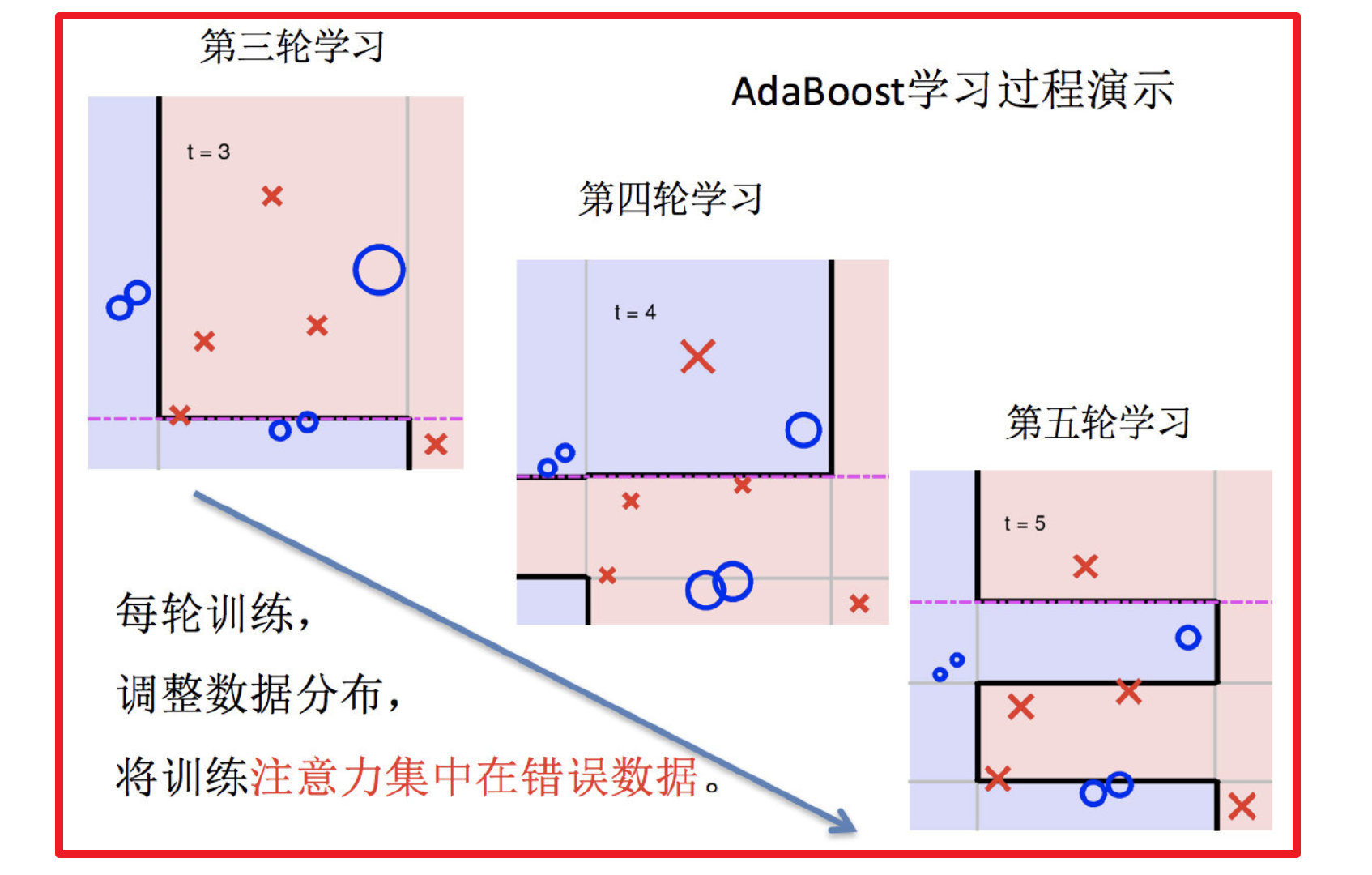
6.整体过程实现

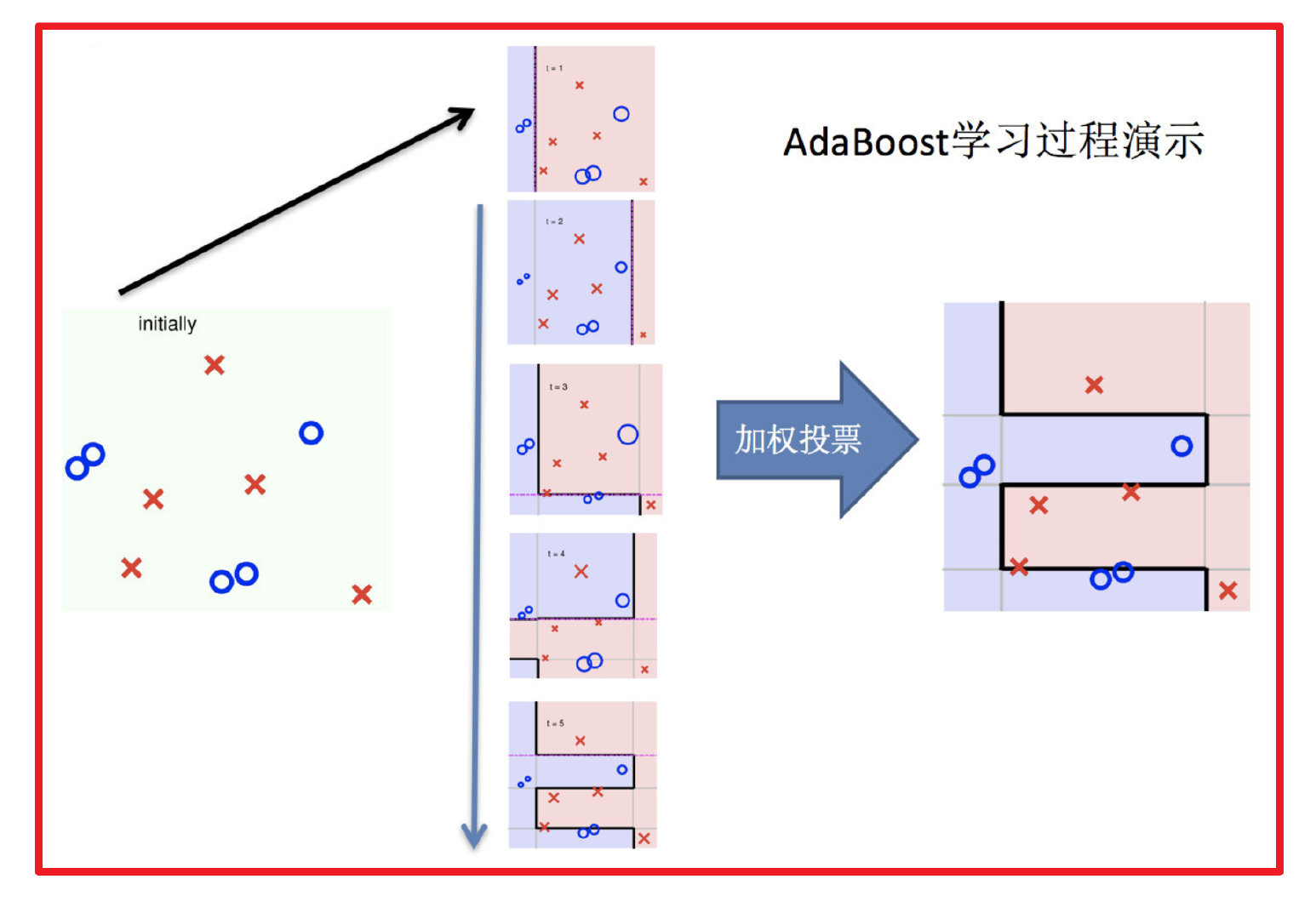
3 bagging集成与boosting集成的区别：

区别一:数据方面
- Bagging：对数据进行采样训练；
- Boosting：根据前一轮学习结果调整数据的重要性。
区别二:投票方面
- Bagging：所有学习器平权投票；
- Boosting：对学习器进行加权投票。
区别三:学习顺序
- Bagging的学习是并行的，每个学习器没有依赖关系；
- Boosting学习是串行，学习有先后顺序。
区别四:主要作用
- Bagging主要用于提高泛化性能（解决过拟合，也可以说降低方差）
- Boosting主要用于提高训练精度（解决欠拟合，也可以说降低偏差）

4 AdaBoost介绍

4.1 构造过程细节：

步骤一：初始化训练数据权重相等，训练第一个学习器。
- 该假设每个训练样本在基分类器的学习中作用相同，这一假设可以保证第一步能够在原始数据上学习基本分类器 $H_1(x)$
步骤二：AdaBoost反复学习基本分类器，在每一轮m=1,2,…,M顺次的执行下列操作：
- （a）在权值分布为 $D_t$ 的训练数据上，确定基分类器,（刚开始每个数据的权重都是1/N，N为数据的个数）；
- （b）计算该学习器在训练数据中的错误率，h为预测值，y为真实值：
  
  $\varepsilon _t = P(h_t(x_t)\neq y_t)$
- （c）计算该学习器的投票权重(该系数是这个分类器用于最终的分类器集成时的系数。)：
  
  $\alpha _t=\frac{1}{2}ln(\frac{1-\varepsilon _t}{\varepsilon _t})$
- （d）根据投票权重，对训练数据重新赋权（ $D_t$ 是第t轮每个数据的权重分布）, $Z_t$ 为归一化系数，公式为
  $\sum_t D_t(x)* \begin{cases} e^{-\alpha_t} ,预测值=真实值 \\ e^{\alpha_t} ，预测值\not=真实值\\ \end{cases}$