【连载】第三章刚体的定轴转动第一节——刚体定轴转动的角量描述

我是灼灼，一只初学Java的大一金渐层。
向往余秀华和狄兰·托马斯的疯狂，时常沉溺于将情感以诗相寄；追逐过王尔德、王小波的文字，后陷于毛姆和斯蒂芬·金不可自拔；热爱文学的浪潮，白日梦到底却总在现实里清醒；艳羡平静又极度渴盼奔跑的力量。
欢迎与我交流鸭· QQ:1517526827；
个人博客：https://blog.csdn.net/weixin_52777510?spm=1001.2101.3001.5343

大学物理——教材：大学物理第六版

第三章|刚体的定轴转动（相关内容）
【连载】第一节 刚体定轴转动的角量描述
【连载】第二节 转动惯量 刚体定轴转动定律
【连载】第三节 定轴转动刚体的角动量守恒定律

第三章 刚体的定轴转动

• 第一章 质点运动学——研究如何描述物体的运动状态

  • 位置、位移x、速度v、加速度a
  • 角位移、角速度ω、角加速度β及其关系

• 第二章 质点动力学——研究物体之间相互作用与运动状态关系

  • 力F、速度v、加速度a、冲量I、动量p、角动量、能量E、动能Ek、势能E及其关系

3-1 刚体定轴转动的角量描述

一、刚体的平动与转动

1.刚体

在外力的作用下,形状和大小不发生变化的物体

• 在运动中刚体内任意两点间的距离都保持不变
• 刚体是一种理想化的物理模型
• 刚体可看成是由许多相对位置不变的质点组成的物体
• 如果研究对象的形变可以忽略，则可以近似看作刚体处理

2.刚体的平动

刚体中任意两点的连线AB,在运动过程中始终保持平行

平动举例：

证明上图：

刚体中任意点的速度、加速度在运动过程中始终相同
研究刚体的平动==>质心的运动（质点的运动）

3.定轴转动

转动—— 刚体中各点都绕同一直线作圆周运动

定轴转动——转轴的位置和方向固定不变的转动

定轴转动刚体的各点,在同一时间内,对轴的转角相等，角速度和角加速度都相等。

刚体的转动可以用角量描述

本课程只讨论刚体的定轴转动~

4.刚体的运动

刚体的一般运动=质心的运动+绕质心的转动。

二、刚体定轴转动的描述

1.基本概念

转动平面：过刚体上某点p垂直于转轴的平面。

转动中心：转动平面与轴的交点 o

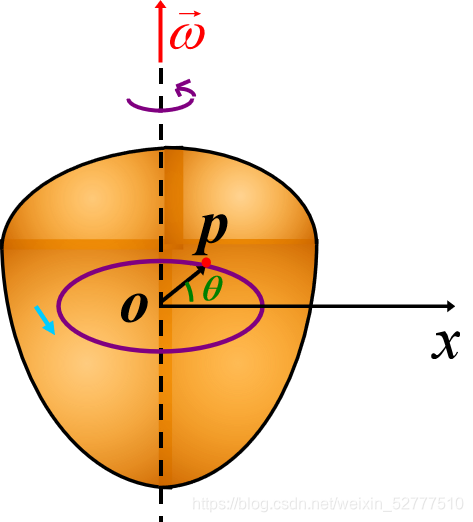
分析图得：

• 角速度方向向上，刚体的运动可以以刚体内任意一点p的运动的角量来描述。
• Op与x轴的夹角θ
• 刚体从上方看为沿逆时针方向旋转

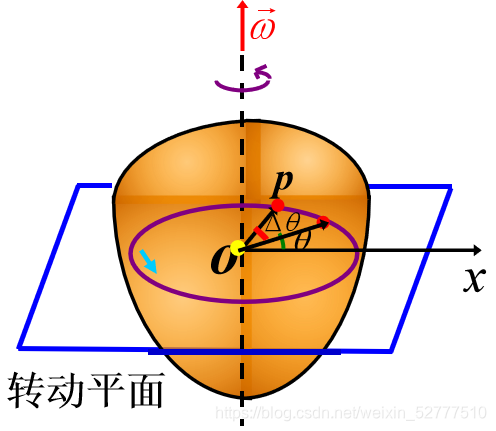
如图：
刚体内任意p点的运动，在转动平面内绕o作圆周运动，且所有点的角量△θ，ω，β相同。
所以可用刚体中任一点p运动的**角量**△θ，ω，β来描述刚体的运动。

2. 角位置θ

如上图为：Op与x轴的夹角θ

3. 角位移

△t时间内刚体角位置的改变量（可以看作是角度的变换）

如图：

• p点转过了 △θ角度，用时△t
  
  角位置初始值和最终值表示：
  
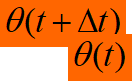
  公式：
  

4. 角速度矢量
   
   方向：沿转轴（右手螺旋方向）

• 角速度矢量的表示：

5. 角加速度矢量

大小：

方向：沿转轴如图——

• 即β>0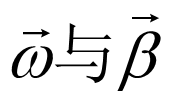方向相反，减速转动 。
• 即β<0

三、刚体的匀变速转动

当刚体绕定轴转动的角加速度β为**恒量**时，刚体做匀变速转动 . 

刚体匀变速转动与质点匀变速直线运动公式对比——

只是换字母的不同~

四、角量与线量的关系

若刚体以角速度ω转动，对任一点P：位置矢量r, 速度v，




刚体中任一点线量与角量的关系

两个重要的关系：


重点公式！！！



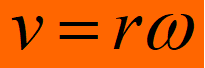
练习题：

M=kωʌ2=Jβ