（LeetCode）376. 摆动序列

题目来源：

376. 摆动序列 - 力扣（LeetCode）

---

题目内容：

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列 。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

• 例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

• 相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度

示例 1：

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2：

输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

示例 3：

输入：nums = [1,2,3,4,5,6,7,8,9]
输出：2

---

思路分析：

贪心算法：（也可以用动态规划来做）

题解来源（视频讲解）：贪心算法，寻找摆动有细节！| LeetCode：376.摆动序列_哔哩哔哩_bilibili 

（大家可以去B站关注这个宝藏博主！）

分三种情况（很难一次性全部想到）：

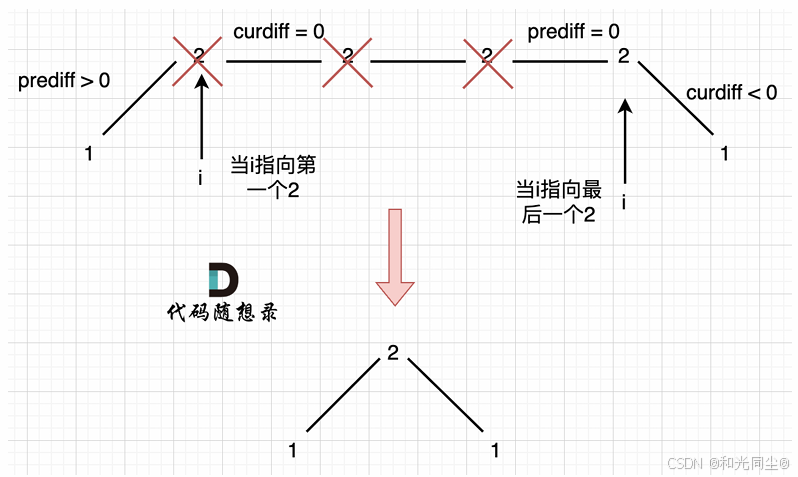
• 情况⼀：上下坡中有平坡

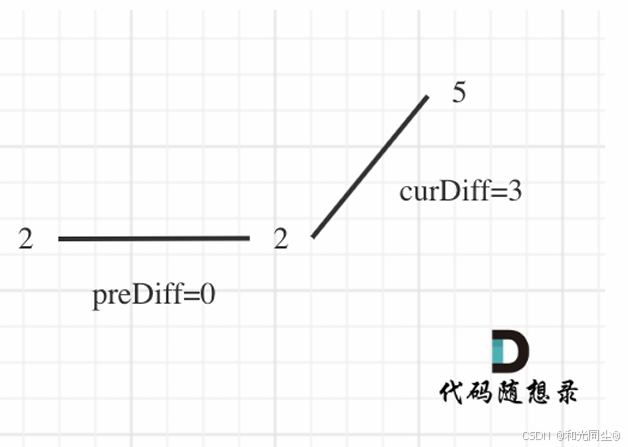
• 情况⼆：数组⾸尾两端

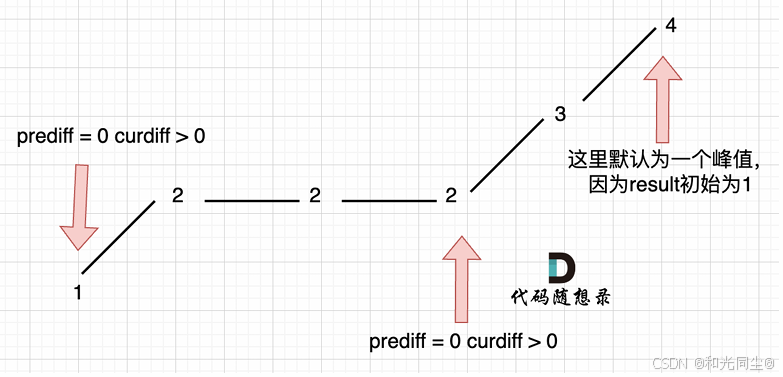
• 情况三：单调坡度有平坡

• 废话不多说，上图！（这里也是借用上面那个宝藏博主的图片）

• 情况一：上下坡中有平坡
  

• 情况⼆：数组⾸尾两端
  

• 情况三：单调坡度有平坡
  

代码实现：

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        if(nums.size()<=1) return nums.size();
        int nowDiff=0;//当前一对差值
        int preDiff=0;//前一对差值
        int result=1;//记录峰值个数，默认序列最右边有一个
        for(int i=0;i<nums.size()-1;i++){
            nowDiff=nums[i+1]-nums[i];
            //出现峰值.(峰值就是满足条件的情况)
            if((preDiff<=0&&nowDiff>0)||(preDiff>=0&&nowDiff<0)){
                result++;
                preDiff=nowDiff;
            }
        }
        return result;
    }
};

题目心得：

• 不知你是否遇到过这样一种情况，面对冗长的思路分析，觉得无从下手/看不进去
• 推荐你先去照着敲一遍代码（过程中大脑会自动的试着去理解）然后再去看思路分析，对题目有了整体的把握之后再去进行总结