【数据结构C语言版本】王阳明格竹，周树皮说树||细说HuffmanTree（附完整代码）

最新推荐文章于 2025-04-24 10:32:27 发布
最新推荐文章于 2025-04-24 10:32:27 发布
阅读量1k 收藏 1
点赞数 4
分类专栏： 数据结构C语言 文章标签： 数据结构 c语言 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_53116058/article/details/121536888
版权
本文档详细介绍了Huffman树的创建原理和手动操作步骤，包括术前准备、上机实操、存储结构设计、排序选择以及纯纯的数组操作。作者通过实例展示了如何构建Huffman树，并分享了在编程实现过程中的调试经验，虽然最终未能输出预期结果，但完整代码和测试结果已给出，可供进一步研究。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

目录

写在前面

现在时间是2021年11月25日下午2:24，在花费一晚上加两节自习加中午没睡觉，Joe树皮终于实现了她的HuffmanTree，中间N次调试发现错误的时候都让我很是怀疑，我是周树皮，不是周木头，错得我离谱，改得我吐血。
无语，快上课了，文章先开个头，后续会更新HuffmanTree的实现原理，顺便分享一下我的心酸调试过程（已鸽）。
发现我已经语无伦次了，管他管他我说的就是病句
555555想睡觉觉！！！！！！！！

1.术前准备

1.1 saysay原理

Huffman Tree的创建原理，很简单，一句话就是：从当前所有节点中选出权重最小与权重次小的两个结点将它们的合并为新结点，新结点的权重为两个结点权重之和，并用新结点替换最小与次小结点，重复进行此过程，直到只剩下一个结点；我们惊奇得发现：结点两两融合形成新结点并被替换，最终新结点数目为初始结点数-1，故总结点数目为2*初始结点数-1。（数学知识，自己推去）

hhhhhhhh好长啊，看我一句话，胜似一段话SOS
阿巴阿巴阿巴总结下挽回尊严？

纵观全程，我们要做的其实就是：

挑选->融合->替换，直到只剩下一个结点！！！！

（棒！（我觉得）精辟！）

1.2 手工操作Huffman Graph

接下来请读者跟着俺一起来play play 介个Huffman Graph

1）初始化整表结构

  1. 我们假设初始结点数目（NodeNum）为3，并规定结点数目为下标（index），每个结点需记录：权重（weight）、父结点（parent）、左孩子结点（lchild）、右孩子结点（rchild）这五个信息作为表头。

  2. 根据公式可得：新创建结点数为2，总结点数（TotalNode）为5，即index最大为5。

  3. 当前所有结点未被赋值，初始化时所有数据全部置零。

操作结束，我们创建了如下这张Huffman Graph：
在这里插入图片描述
2）初始结点权重赋值

依次将3个初始结点的权重（weight）赋值为1、2、3

我们便可得到如下Huffman Graph：
在这里插入图片描述
3）挑选所有节点中权重（weight）最小与次小的结点

新结点操作：

  1. 权重（weight）更新为最小结点与次小结点权重之和
  2. 左孩子（lchild）更新为最小结点
  3. 右孩子（rchild）更新为次小结点

次小最小结点操作：

  1. 父结点（parent）更新为新结点

更新后Huffman Graph如下图：
在这里插入图片描述
4.重复第3步操作直到更新完index=5结点（TotalNode）的各项数据。

Huffman Graph 生成！
在这里插入图片描述

2.上机实操带你写个Bug

2.1 存储结构设计
远看山有色，近听水无声

横向看生成的Huffman Graph，将index栏看成对应下标的结点，会发现每个结点都存储着相同的四种信息：权重（weight）、父结点（parent）、左孩子结点（lchild）、右孩子结点（rchild）。
于是手工操作的Huffman Graph在计算机看来就等效成图二的形态，显而易见，其存储结构就是一个结构体数组。而之后所有的操作，其实就是基于结构体数组各存储单元的操作。
在这里插入图片描述
这里，我们将结构体的一个存储单元提取出来，此操作对应在Huffman Graph上就是取出对应行。
结构体数组
Huffman Graph
到这里，我相信读者应该能很容易得定义出单个结点（HuffNode）的存储结构了吧！

typedef struct Node{
	
	int weight;//权重
	int parent;//父结点
	int lchild;//左孩子
	int rchild;//右孩子
		
}HuffNode;

为了程序的可读性，Joe树皮模仿了栈的存储结构封装了一个Huffman Graph的存储结构，该栈包含一个数组下标（index）以及一个用于存储HuffmanNode类型结点的结构体数组（Tree[MAXSIZE]）

// Huffman树数组结构

typedef struct Tarry{
	
	HuffNode Tree[MAXSIZE];			//用于存储结点的数组 
	int index;					  	//用于数组下标 
	
}HuffTree;

在所有操作开始前，我们需在main函数中定义一个HuffTree类型的指针变量（HFTree）并将它初始化：1）动态分配内存空间 2）初始化下标（index）。
之后我们便可以用 HFTree->Tree[]表示结构体数组，用HFTree->index表示数组下标，HFTree->Tree[HFTree->index]便可以表示对应结点，再用HFTree->Tree[HFTree->index].x(x为weight、lchild、rchild、parent)表示该结点存储的对应数据了。

2.2 排序选择
2.2.1 变量声明
	int min1,min2,x1,x2,i,flag=0;	

//min1、min2 分别记录最小值，次小值 
//x1、x2 分别记录最小值下标，次小值下标 
//i	用于内层循环下标，表示此轮比较选择i次
//flag记录每轮新结点的下标
2.2.1 可恶的下标

先来分析i（此轮选择次数）、NodeNum（初始结点数）、TotalNode（总结点数）之间的关系。
前面我们已经明确：TotalNode=2*NodeNum-1
下图也能清楚看出初始化状态时二者的关系，
在这里插入图片描述
接着，我们将过程展开，并将公式变形为：TotalNode=NodeNum+NodeNum’-1

令:
TotalNode表示当前总结点数（初始结点+当前新生成结点）
NodeNum表示初始结点数
NodeNum’表示当前初始结点数（初始结点数+当前生成结点数）
NodeNum’-1则表示新生成结点数

到这里，我们会发现，整个重复的选择比较操作存在两个变量：当前总结点数，当前初始结点数。因此我们需要用一个双层for循环进行解决。
在这里插入图片描述
从前面的分析可知，当前总结点数受当前新生成结点的控制，因此，当前新生成结点数（NodeNum-1）应为外层循环；内层循环内，我们需要遍历当前初始结点（NodeNum’）以找到最小与次小结点，直到更新完所有结点的weight。

需明确！内层循环我们实现的是当前初始结点的比较，因此，for执行次数为当前总结点数-1，清楚认识这点在之后代码实现中定义for循环终止条件设定时十分重要！

用伪代码表示即：
for（index=第一个结点；index=第一个结点:当前新生成结点,index++）{
for(i=第一个结点；i=第一个结点：当前总结点；i++){
比较选择
}
}

代码实现如下：

	for((*HFTree)->index=1;	(*HFTree)->index<NodeNum;(*HFTree)->index++)
	{
		for(i=1;i<NodeNum+(*HFTree)->index;i++){	
		挑选比较
		}
}
2.2.2 小孩子才做选择，次小最小我全都要

首先，在每轮内层循环开始前，我们需将min1、min2初始为MaxValue，该操作使循环执行后min1、min2一定会被重新赋值；将x1、x2初始为0，防止对新生成结点下标产生影响。

在内层循环中，我们对每个还未融合（无父结点）结点的权重进行如下比较：
在这里插入图片描述
1）Tree[i].weight<min1

  1. 原最小权重成为次小权重 min2=min1
  2. 更新最小权重 min1=Tree[i].weight
  3. 原最小下标成为次小下标
  4. 更新最小下标

2）min1<Tree[i].weight<min2

  1. 更新次小权重 min2=Tree[i].weight
  2. 更新最小下标 x2=i

3）Tree[i].weight>min2

无需改动

代码实现如下

	//挑选次小最小构建新结点
	
	int min1,min2,x1,x2,flag=0;	//规定min1记录最小值
	int i; 					//	用于内层循环下标 
		//初始化min1 min2都为最大值（防止第一个权重最小最后 两个结点一样 

	
	for((*HFTree)->index=1;	(*HFTree)->index<NodeNum;(*HFTree)->index++){
		min1=min2=MaxValue;		
		x1=x2=0;
		//新创建结点下标为NodeNum+当前index 
		printf("index=%d\n",(*HFTree)->index);
			for(i=1;i<NodeNum+(*HFTree)->index;i++){
				printf("i=%d\n",i);
					//(1)如果当前权重小于最小权重 则更新最小 原最小成为次小 
					//已使用的结点跳过 
					printf("0.x1=%d x1=%d\n",x1,x2);
				if((*HFTree)->Tree[i].parent==0&&(*HFTree)->Tree[i].weight<min1){
					//原最小成为次小 
					min2=min1;		
					x2=x1;
					//更新最小
					min1=(*HFTree)->Tree[i].weight;
					x1=i;
					printf("1.x1=%d x2=%d\n",x1,x2);
					printf("1.min1=%d min2=%d \n",min1,min2); 
				}
		
				//当前权重大于最小小于次小 记录为次小 
				else
					if((*HFTree)->Tree[i].parent==0&&(*HFTree)->Tree[i].weight<min2){
						min2=(*HFTree)->Tree[i].weight;
						x2=i;	
						printf("2.x1=%d x2=%d",x1,x2);	
						printf("1.min1=%d min2=%d \n",min1,min2); 
				}
														//新结点左孩子 			
		}
2.3 纯纯的数组操作
2.3.1 新结点赋值还不是有手就行
  1. 记录当前创建结点下标 flag=Tree->index+NodeNum
  2. 新结点权重=最小结点权重+次小结点权重
  3. 新节点左孩子为最小结点下标
  4. 新节点右孩子为次小结点下标
  5. 最小结点父节点为新节点
  6. 次小结点父节点为新节点

代码实现如下：

flag=(*HFTree)->index+NodeNum;//当前创建结点下标				
		    //挑选结点的父结点记录 
	    	(*HFTree)->Tree[x1].parent=flag;
	    	(*HFTree)->Tree[x2].parent=flag;
	    	printf("flag=%d\n",flag);
	    	printf("x1=%d,x2=%d\n",x1,x2);
2.3.2打印Huffman Graph 还不是有键盘就行

循环初始条件： 从第一个结点开始（Tree->index=1）
循环终止条件： 到总结点数结束（Tree->index=TotalNode）
循环执行操作：输出index对应结点的各个数据

加点细节\t \n 表头，搞定输出！

void PrintHuffmanTree(HuffTree *HFTree,int TotalNode)
{
	HuffNode *PNode=(HuffNode*)malloc(sizeof(HuffNode));		//用于指向当前操作结点
	//输出表头 
	printf("\t\tHuffman Graph\t\t\n"); 
	printf("index\t weight\t parent\t lchild\t rchlid\t\n ");
	printf("\n");
	for(HFTree->index=1;HFTree->index<=TotalNode;HFTree->index++){
		PNode=&(HFTree->Tree[HFTree->index]);					//PNode指向当前操作数组单元
		printf(" %d\t  %d\t  %d\t  %d\t  %d\t\n ",HFTree->index,PNode->weight,PNode->parent,PNode->lchild,PNode->rchild);
		printf("\n");
	}	
}
3.De个Bug

鸽了hh

4.附录

4.1完整代码
#include<stdio.h>
#include<malloc.h>
 
#define MAXSIZE 50
#define MaxValue 1000

//Huffman结点结构

typedef struct Node{
	
	int weight;//权重
	int parent;//父结点
	int lchild;//左孩子
	int rchild;//右孩子
		
}HuffNode; 

// Huffman树数组结构

typedef struct Tarry{
	
	HuffNode Tree[MAXSIZE];			//用于存储结点的数组 
	int index;					  	//用于数组下标 
	
}HuffTree;

//Huffman树的初始化 

//定义从数组第二个元素开始存储 即数组下标为1开始 
void HuffmanTreeInit(HuffTree **HFTree,int TotalNode)
{
	(*HFTree)=(HuffTree*)malloc((TotalNode+1)*sizeof(HuffNode));//分配存储空间 
	(*HFTree)->index=-1;								//初始化下标 
} 
 
 
void CreatHuffmanTree(HuffTree **HFTree,int NodeNum,int TotalNode)
{	
	HuffNode *PNode=(HuffNode*)malloc(sizeof(HuffNode));		//用于指向当前操作结点

	//初始化赋值 

	printf("请依次输入%d个结点的权值:\n",NodeNum);
	for((*HFTree)->index=1;	(*HFTree)->index<=TotalNode;(*HFTree)->index++){
		PNode=&(*HFTree)->Tree[(*HFTree)->index];				//PNode指向当前操作数组单元 记得&！！！！！ 
		
		//初始结点权重赋值 
		if((*HFTree)->index<=NodeNum){
			scanf("%d",&PNode->weight);
		}
		else{
			PNode->weight=0; 		
		}
		//左孩子、右孩子、父节点赋值
		PNode->parent=0;
		PNode->lchild=0;
		PNode->rchild=0;
	} 
	
	//挑选次小最小构建新结点	
	int min1,min2,x1,x2,flag=0;	//规定min1记录最小值
	int i; 					//	用于内层循环下标 

	//初始化min1 min2都为最大值 防止第一个权重最小导致最后两个结点一样都为第一个 
	//里层for循环结束需要重新赋值min啊救命！！！！ 

	
	for((*HFTree)->index=1;	(*HFTree)->index<NodeNum;(*HFTree)->index++){
		min1=min2=MaxValue;		
		x1=x2=0;
		//新创建结点下标为NodeNum+当前index 
			for(i=1;i<NodeNum+(*HFTree)->index;i++){
		//(1)如果当前权重小于最小权重 则更新最小 原最小成为次小 
					//已使用的结点跳过 
				if((*HFTree)->Tree[i].parent==0&&(*HFTree)->Tree[i].weight<min1){
					//原最小成为次小 
					min2=min1;		
					x2=x1;
					//更新最小
					min1=(*HFTree)->Tree[i].weight;
					x1=i;
				}	
		//（2）当前权重大于最小小于次小 记录为次小 
				else
					if((*HFTree)->Tree[i].parent==0&&(*HFTree)->Tree[i].weight<min2){
						min2=(*HFTree)->Tree[i].weight;
						x2=i;	
				}
														//新结点左孩子 			
		}
		    flag=(*HFTree)->index+NodeNum;//当前创建结点下标				
		    //挑选结点的父结点记录 
	    	(*HFTree)->Tree[x1].parent=flag;
	    	(*HFTree)->Tree[x2].parent=flag;
	    
	    	//新结点创建 
		    (*HFTree)->Tree[flag].weight=(*HFTree)->Tree[x1].weight+(*HFTree)->Tree[x2].weight;//新结点权重 
	    	(*HFTree)->Tree[flag].lchild=x1;												//新结点左孩子 
	    	(*HFTree)->Tree[flag].rchild=x2;	
						
	} 	
	printf("\n"); 
} 

void PrintHuffmanTree(HuffTree *HFTree,int TotalNode)
{
	HuffNode *PNode=(HuffNode*)malloc(sizeof(HuffNode));		//用于指向当前操作结点
	//输出表头 
	printf("\t\tHuffman Graph\t\t\n"); 
	printf("index\t weight\t parent\t lchild\t rchlid\t\n ");
	printf("\n");
	for(HFTree->index=1;HFTree->index<=TotalNode;HFTree->index++){
		PNode=&(HFTree->Tree[HFTree->index]);					//PNode指向当前操作数组单元
		printf(" %d\t  %d\t  %d\t  %d\t  %d\t\n ",HFTree->index,PNode->weight,PNode->parent,PNode->lchild,PNode->rchild);
		printf("\n");
	}	
} 

int main() 
{

	HuffTree *HFTree;	//
	int NodeNum;			//用于记录初始创建结点个数 
	int TotalNode;			//用于记录创建后总结点个数 
	
	printf("请输入创建结点个数：\n");
	scanf("%d",&NodeNum);
	TotalNode=2*NodeNum-1;
		
	HuffmanTreeInit(&HFTree,TotalNode) ;
	CreatHuffmanTree(&HFTree,NodeNum,TotalNode); 
	PrintHuffmanTree(HFTree,TotalNode);
	
	return 0;
}
4.2测试结果

终于实现了！！！！
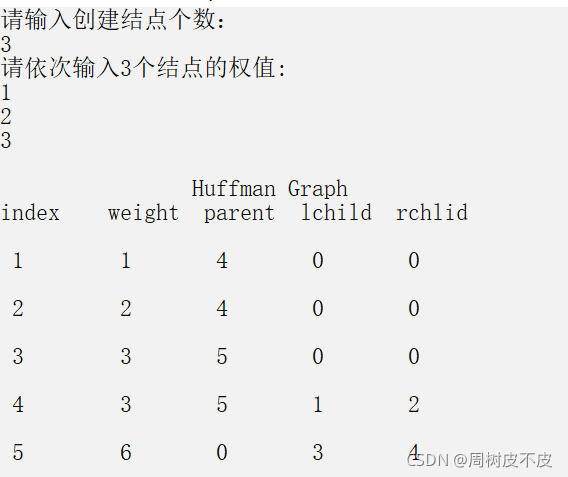
在这里插入图片描述

4.3 总结与展望

无报错，可运行，但是无法输出预期结果，自行查询百度无法解决，询问老师同学无果？

I Don’t Want To Say Goodbye好好听！！！靠这首循环码完这篇!!!yeah!!!发朋友圈啦！！！！！

Huffman编码的设计与实现
qq_43573663的博客
03-27 5380
（一）设计描述 1.题目描述 设计一个利用哈夫曼算法的编码和译码系统，重复地显示并处理以下项目，直到选择退出为止。 1) 输入一串字符，然后统计其中各个字符的个数,即每个字符的权值。 2) 进行初始化操作,并建立哈夫曼树； 3) 编码：利用建好的哈夫曼树生成哈夫曼编码，并输出编码； 4) 译码，即输入每个字符对应的二进制的编码（0或1），然后输出对应的字符。 5) 结束操作。 2.设计目的......
哈夫曼树实现电文编码译码
CD__ordinary_word的博客
01-02 3247
哈夫曼编码实现电文字符串编码电文编码 电文编码 输入的一串电文字符实现哈夫曼编码，再对哈夫曼编码生成的 代码串进行译码，输出电文字符串。即以字符串字母出现次数为权值，生成哈夫曼树。 #include<stdio.h> #include<string.h> #include<stdlib.h> #define MAXSIZE 50 typedef char DataType; typedef struct // 哈夫曼树结点的结构 { DataType data;
数据结构复习
m0_57105024的博客
12-16 1136
#include<stdio.h> #define MAXSIZE 50 typedef int ElemType; typedef struct { Elemtype data[MAXSIZE]; int length; }Sqlist; void InitList(SqList &L) { L.length=0; } void CreateList(SqList &L,int n) { int i=0; printf("输入%d个元素:\n",n); fo
哈夫曼编解码（C语言）
寒泉
10-28 4万+
哈夫曼编解码（C语言） 示例 输入： helllllllo 生成码表： a:00010010 b:00010011 c:00010100 d:00010101 e:001 f:00010110 g:00010111 h:010 i:00011000 j:00011001 k:00011010 l:1 m:00011011 n:00011100 o:011 p:00011101 q:00011110 r:00011111 s:0000000 t:0000001 u:0000010 v:0000011 w:00
数据结构之栈的基本操作（c语言版）
qq_40842211的博客
04-19 506
//栈的顺序存储 #include<stdio.h> #include<stdbool.h> #define MaxSize 50 #define ElemType char typedef struct{ ElemType data[MaxSize]; int top; }SqStack; //栈的初始化 void InitStack(SqStac...
HUFF文件连续输入.rar_UHX_对于学习哈夫曼树非常有用加深理解_数据结构Huffman树的构造代码
09-21
哈夫曼树（Huffman Tree），也称为最优二叉树，是数据结构中一种非常重要的树形数据结构，尤其在数据压缩领域应用广泛。哈夫曼树是通过一种特殊的构造方法，即哈夫曼编码（Huffman Coding）来实现的。这种编码方式是...
huffman树_Huffman树_C++_huffman_数据结构_
10-02
哈夫曼树（Huffman Tree），也称为最优二叉树，是数据压缩中常用的一种数据结构。它是一种带权路径长度最短的二叉树，由哈夫曼在1952年提出，用于解决“最小带权路径长度”问题。在哈夫曼树中，频率较高的字符对应的...
王道数据结构+C语言版+超全笔记(图文)+个人整理版本
04-05
(一)数据元素、数据结构、抽象数据类型等概念 (二)算法设计的基本要求 (三)语句的频度和估算时间复杂度 二、线性表 (一)线性表的定义和基本操作 (二)线性表的实现 1.顺序存储结构 2.链式存储结构 3.线性表的应用 三...
数据结构C语言代码示例，有详细注释
02-16
数据结构C语言 单链表 0_SingleLinkList.c 双链表 1_DualLinkList.c 递归 2_Recursion.c 栈 3_Stack.c 汉诺塔 4_Hanoi.c 二叉树 5_BinaryTree.c 最小堆 6_MinHeap.c 哈夫曼树 7_HuffmanTree.c 邻接...
c语言c++项目源代码_链表HuffmanTree.rar
03-27
**HuffmanTree：C/C++实现的链表压缩算法库** HuffmanTree是一个基于C/C++编写的链表压缩算法库，专注于提供高效、易用的数据压缩解决方案。它采用Huffman编码算法，这是一种广泛应用于数据压缩的熵编码方法，能够...
STM32CubeMX学习笔记（51）——读写内部Flash
Leung的博客
02-07 9662
在STM32芯片内部有一个 FLASH 存储器，它主要用于存储代码，我们在电脑上编写好应用程序后，使用下载器把编译后的代码文件烧录到该内部 FLASH 中，由于 FLASH 存储器的内容在掉电后不会丢失，芯片重新上电复位后，内核可从内部 FLASH 中加载代码并运行。STM32 的内部 FLASH 包含主存储器、系统存储器以及选项字节区域，它们的地址分布及大小见下表。
sizeof的使用
ugvihc的专栏
11-10 5146
sizeof- -      sizeof的定义——sizeof的结果等于对象或者类型所占的内存字节数                                 关键字：sizeof，字节对齐，多继承，虚拟继承，成员函数指针前向声明：本来我对SIZEOF()只有一个小小的问题,通读此文,才发现它的博大精深,在此感谢lostinmymind!我把它贴在这里,和朋友们共享
哈夫曼树(Huffman树)原理分析及实现（C++）
Garen的博客
01-07 3639
1 构造原理 假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为： 　　(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)； 　　(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和； 　　(3)从森林中删除选取的两棵树，并将新树加入森林； 　　(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。 显然对n个权值，构造哈夫曼
【数据结构】哈夫曼树及哈夫曼编码实现（C语言）
热门推荐
weixin_51450101的博客
02-12 6万+
目录1. 哈夫曼树1.1 基本概念1.2 构造哈夫曼树1.3 哈夫曼树的类型定义1.4 哈夫曼树创建的算法实现2. 哈夫曼编码实现2.1 哈夫曼编码2.2 完整代码2.3 运行结果 1. 哈夫曼树 1.1 基本概念 路径：指从根结点到该结点的分支序列。 路径长度：指根结点到该结点所经过的分支数目。 结点的带权路径长度：从树根到某一结点的路径长度与该结点的权的乘积。 树的带权路径长度(WPL)：树中从根到所有叶子结点的各个带权路径长度之和。 哈夫曼树是由 n 个带权叶子结点构成的所有二叉树中带权路径长度最短的
C语言实现Huffman Tree（参考严蔚敏《数据结构》部分伪码）
xhj_enen的博客
03-26 899
Huffman树，又称最优二叉树，是一类带权路径最短的树，有着广泛的应用。Huffman树中没有度为1的节点，所以一棵有 n 个叶子节点的 Huffman 树中，总共有 2n-1 个结点。构建赫夫曼树的步骤：1）根据给定的 n 个权值 {w1,w2,w3,...,wn} 构成 n 棵二叉树的集合 F={T1,T2,T3,...,Tn}，其中每棵二叉树 Ti 中只有一个带权为 wi 的根节点，其左右...
数据结构与算法之Huffman tree(赫夫曼树 / 霍夫曼树 / 哈夫曼树 / 最优二叉树)
努力让自己发光，对的人才能迎着光而来
09-05 2万+
赫夫曼树概述 定义 构造赫夫曼树步骤 代码实现
[Java · 铢积寸累] 数据结构 — 数组类型 - 增 & 删 & 改 & 查
Blue17 の 小窝
04-22 577
想系统化学习 Java 编程？在上一章中我们介绍了如何声明与创建数组，还介绍了数组的基本使用方式。本章我们将在上一章的基础上，拓展数组的使用方式（可能会涉及一些思维题）。
Redis中的hash数据结构设置过期时间的坑！！！
最新发布
m0_62458145的博客
04-24 98
在使用 Redis Hash 结构时，发现在异步操作完成后设置过期时间不生效，但在第一次写入后立即设置过期时间却可以正常工作。
评论 8
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

周树皮

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值