科研笔记第19期——K-means聚类（肘部法）

本文链接：https://blog.csdn.net/weixin_53181946/article/details/138396827

一、基于 K-means 的聚类分析步骤

聚类中心的个数K需要事先给定，但实际中K值的选定是非常困难的，很多时候我们并不知道给定的数据集应该聚成多少个类别才最合适。

针对这个缺点，通常我们会根据先前的经验选择一个合适的k值，如果没有先验知识，则可以使用“肘部法”来选择一个合适的k值。计算公式为式（2）。

二、算例分析

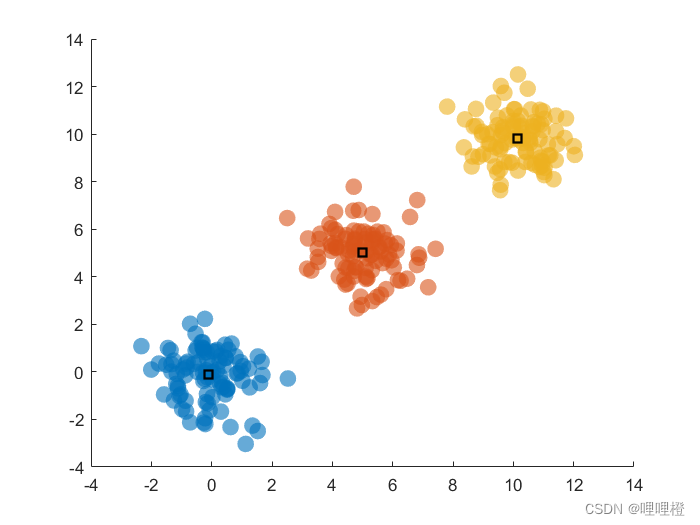
源代码：

主函数：

function [index_cluster,cluster] = kmeans_func(data,cluster_num)
%% 原理推导Kmeans聚类算法
[m,n]=size(data);
cluster=data(randperm(m,cluster_num),:);%从m个点中随机选择cluster_num个点作为初始聚类中心点
epoch_max=1000;%最大次数
therad_lim=0.001;%中心变化阈值
epoch_num=0;
while(epoch_num<epoch_max)
    epoch_num=epoch_num+1;
    % distance1存储每个点到各聚类中心的欧氏距离
    for i=1:cluster_num
        distance=(data-repmat(cluster(i,:),m,1)).^2;
        distance1(:,i)=sqrt(sum(distance'));
    end
    [~,index_cluster]=min(distance1');%index_cluster取值范围1~cluster_num
    % cluster_new存储新的聚类中心
    for j=1:cluster_num
        cluster_new(j,:)=mean(data(find(index_cluster==j),:));
    end
    %如果新的聚类中心和上一轮的聚类中心距离和大于therad_lim，更新聚类中心，否则算法结束
    if (sqrt(sum((cluster_new-cluster).^2))>therad_lim)
        cluster=cluster_new;
    else
        break;
    end
end
end

肘部法子函数：

%% 清空工作区
clear all;
clc;
close all
%% 读取数据
[num,text,raw]=xlsread('数据.xlsx');
figure(1)
plot(num(:,1),num(:,2),'ro','LineWidth',2)
title("原始数据散点图")
%% 肘部法确定聚类数K
SSE=[];
for cluster_num=2:10
    [index_cluster,cluster] = kmeans_func(num,cluster_num);
    a=unique(index_cluster);
    C=cell(1,length(a));
    for i=1:length(a)
        C(1,i)={find(index_cluster==a(i))};
    end
    for j=1:cluster_num
        data_get=num(C{1,j},:);
        distance=(data_get-repmat(cluster(j,:),length(data_get),1)).^2;
        distance1(:,j)=sum(sqrt(sum(distance'))); %类间所有点与该类质心点距离之和
    end
    D(cluster_num,1)=cluster_num;
    D(cluster_num,2)=sum(distance1);
end
figure(2)
plot(D(2:end,1),D(2:end,2))
hold on;
plot(D(2:end,1),D(2:end,2),'or');
xlabel('分类数（K值）');
ylabel('误差平方和');

子函数2：

%% 清空工作区
clear all;
clc;
close all
%% 读取数据
[num,text,raw]=xlsread('数据.xlsx');
figure(1)
plot(num(:,1),num(:,2),'ro','LineWidth',2)
title("原始数据散点图")

cluster_num=3;     %%肘部法确定聚类数K
[index_cluster,cluster] = kmeans_func(num,cluster_num);

%% 画出聚类效果
figure(2)
% subplot(2,1,1)
a=unique(index_cluster); %找出分类出的个数
C=cell(1,length(a));
for i=1:length(a)
   C(1,i)={find(index_cluster==a(i))};
end
for j=1:cluster_num
    data_get=num(C{1,j},:);
    scatter(data_get(:,1),data_get(:,2),100,'filled','MarkerFaceAlpha',.6,'MarkerEdgeAlpha',.9);
    hold on
end
%绘制聚类中心
plot(cluster(:,1),cluster(:,2),'ks','LineWidth',2);