【
目的
】
(1)
掌握利用
DFT
近似计算不同类型信号频谱的原理和方法。
(2)
理解误差产生的原因及减小误差的方法。
(3)
培养学生自主学习能力,以及发现问题、分析问题和解决问题的
能力。
【知识点】
利用
DFT
分析连续信号的频谱
DFT
参数
【背景知识】
声音包括语音、乐音、噪音等。
乐音是发音物体有规律地振动而产生的具有固定音高的音,如
音乐中的
1(Do)
、
2(Re)
、
3(Mi)
。按照音高顺次排列的一串乐音就是音阶,如大家熟悉的
1(Do )2(Re)3(Mi) 4(Fa)5(So)6(La)7(Si)
就是音阶
。乐音由不同频率的正弦信号构成,其最简单的数学
模型是
cos(2
ft
)
,如
C
大调音阶各乐音对应的频率如下表:

【
题目分析和方案设计
】
题目一:
利用
DFT
分析
x
(
t
)=
A
cos(2
f
1
t
)+
B
sin(2
f
2
t
)
的频谱,其中
f
1
=200Hz
,
f
2
=220Hz
。
(1)A=B=1;
(2)A=1,B=0.1
。
分析题目,给出合适的
DFT
参数,并对实验结果进行分析,讨论窗口的长度和窗口的类型对谱
分析有何影响。
(
1)参数确定:
已知连续周期信号
x
(
t
)=
A
cos(2
f
1
t
)+
B
sin(2
f
2
t
)
,其中
f
1
=200Hz
,
f
2
=220Hz
。
① 对信号采样:
由时域离散化频域周期化可知
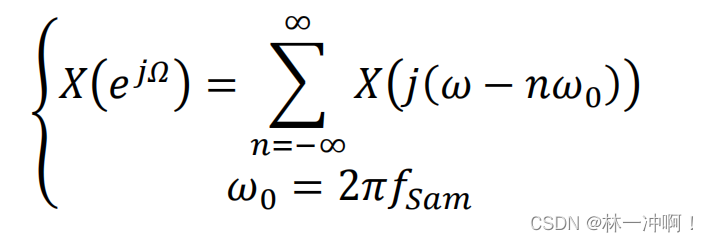
为了避免频谱重叠
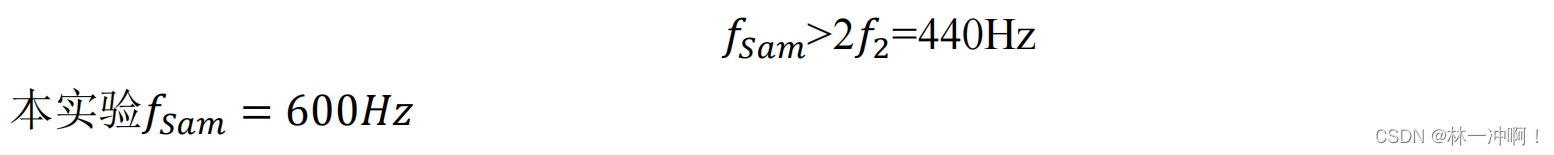
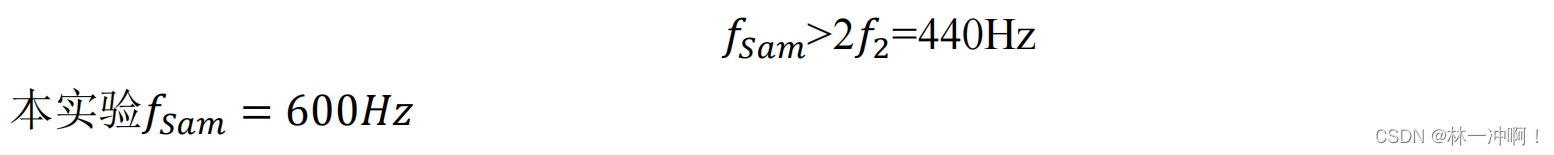
② 窗函数
N 的确定:(矩形窗为例) 已知该信号有两个相邻频率 f
1
=200Hz
,
f
2
=220Hz。
![]()
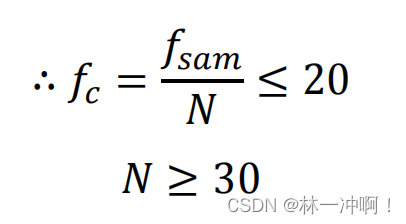
本实验选择
N=30
、
60
、
90
、
120
,分别观察不同窗函数长度对 DFT 计算频谱的结果影响。
③ 窗函数类型的确定
已知不同类型的窗函数截取的 X
N
(e
jΩ
)主瓣峰值和旁瓣峰值之比不同。并且主瓣越宽,旁瓣峰值越衰减。而本实验(2)中,信号存在不同幅值的两个相邻频率,应该重点减小主瓣峰值和旁瓣峰值之比。本次实验我们选择用"矩形窗","海明窗","汉宁窗","布莱克曼窗"和"凯瑟窗",观察不同窗函数处理后 XN(ejΩ
)的频谱。
④ DFT 计算中 L 的确定:
为了减少栅栏效应的影响,应该将 X
N
[k]补零至 L(L>N)。本实验我们选择 L=512.
(2)程序分析:
将两种频率系数、四种取样长度 N 和五种窗口类型进行组合对比,在 DFT 长度不变情况下观察
各组参数对 DFT 频率分析的影响。
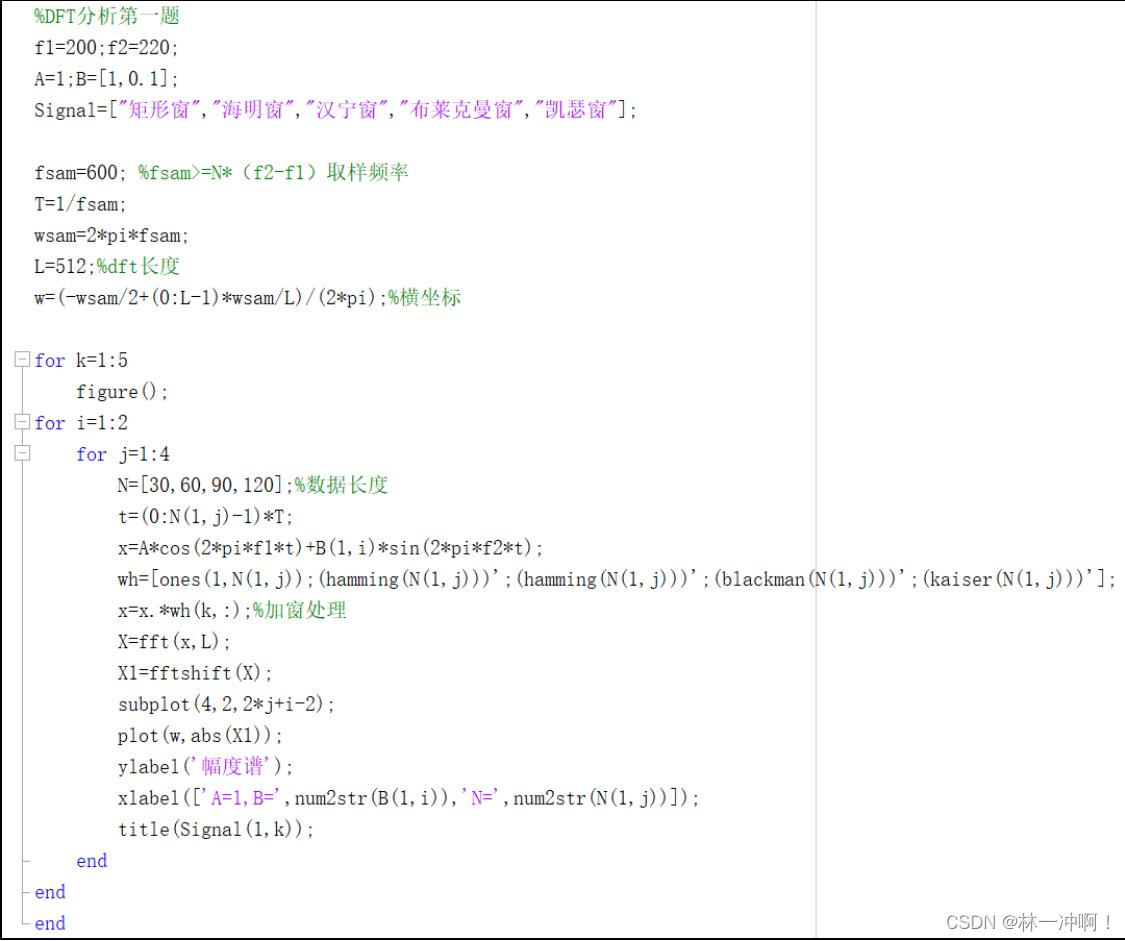

由于复制会变形,本文中只给出题目一的解答,以下问题的解答直接上传资源
题目二:
已知一离散序列为
x
[
k
]=cos(
0
k
)+0.6cos(
1
k
),
其中
0
=12
,
1
=
/64
。
(1)
数据
x
[
k
]
的长度
N
=64
,对
x
[
k
]
做
L
=64
点
FFT,
画出此时信号的频谱,观察是否可以分辨两
个谱峰。若不可以,对
64
点信号补零,画出
L=128
以及
L=512
时信号的频谱,观察是否可以分辨
出两个谱峰,并解释原因。
(2)
选择合适的参数实现题
2
中两个谱峰的分离。
题目三:
利用
DFT
分析音阶信号
yueyin1.wav
的频谱。
要求读取该信号的抽样频率,获得时域抽样点数
N
,确定信号的持续时间以及合适的
DFT
点
数,并根据谱分析的结果,判断是什么调的音阶。
题目四:
和弦的频谱成分。
和弦一般由
3
个(也可大于
3
个)具有一定规律的乐音构成,即
x
(
t
)= cos(2
f
1
t
)+ cos(2
f
2
t
)+
cos(2
f
3
t
)
。
(
1
)利用
DFT
分析和弦信号
hexian1.wav
的频谱,确定构成该和弦的是哪几个乐音(即什么
频率分量)。
(
2
)若乐曲全音符的持续时间为
0.2s,
从理论上分析利用
DFT
分析
16
分音符乐音构成会出现
什么问题?设计实验验证一下你的判断,并给出解决问题的方案。
题目五:
含谐波音阶的谱分析。
优美动听的音乐,其乐音除含有基波频率外还含有若干次谐波频率分量,其数学模型可近似表
示为
。利用
DFT
分析音阶信号
yueyin2.wav
的频谱,能否直接从频谱图确
定各乐音的频谱构成吗?若不能,请给出如何确定各乐音频谱构成的方法,并通过实验验证。





















 1767
1767

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










