文章目录
零、导言
很多问题需要用到图论的相关知识来解题,比如单源最短路算法中的 Diskstra 算法、A* 算法,多源最短路中的 Floyd 算法等等。这些算法的基础就需要建立相关的图,在图的基础上才能解决题目。
下面就先回顾一下图论的相关知识。
一、图论知识
1、什么是图
图是由顶点集合和顶点之间的边集合组成。通常表示为 G(V, E) \texttt{G(V, E)} G(V, E),其中 G \texttt{G} G 表示的就是一个图, V \texttt{V} V 表示的是顶点的集合, E \texttt{E} E 表示的是边的集合。
2、图的各种定义
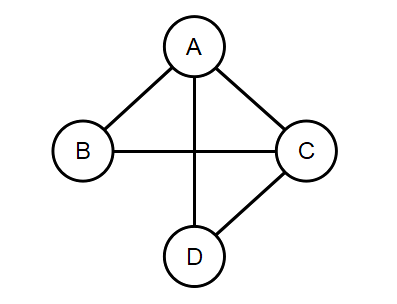
- 无向图:图中任意两个顶点之间的边都是无向边,那么这样的图就称为无向图。那么什么是无向边呢?若顶点
u
\texttt{u}
u 到顶点
v
\texttt{v}
v 之间的边没有方向,可以相互到达,则称这条边为 无向边 ,可以用无序偶对
(u,
v)
\texttt{(u, v)}
(u, v) 表示。如图1所示。
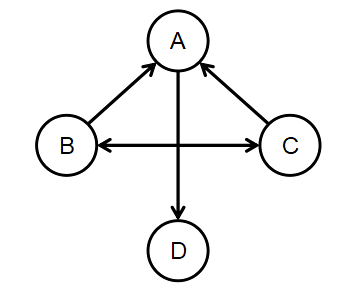
无序偶对 (B, A) \texttt{(B, A)} (B, A) 表示顶点 B \texttt{B} B 和顶点 A \texttt{A} A 之间没有边。 - 有向图:图中任意两个顶点之间的边都是有向边,那么这样的图就称为有向图。那么什么是有向边呢?若顶点 u \texttt{u} u 到顶点 v \texttt{v} v 之间的边有方向,只可以单向到达,则称这条边为 有向边,也称为 弧,可以用有序偶对 <u, v> \texttt{<u, v>} <u, v> 表示。其中 u \texttt{u} u 称为 弧尾 , v \texttt{v} v 称为 弧头 。如图2所示。有序偶对 <B, A> \texttt{<B, A>} <B, A> 表示顶点 B \texttt{B} B 和顶点 A \texttt{A} A 之间有边, B \texttt{B} B 可以到达 A \texttt{A} A,但是 A \texttt{A} A 不可以到达 B \texttt{B} B,只可以单向导通。其中 B \texttt{B} B 是弧尾, A \texttt{A} A 是弧头。
|
|
- 无向完全图:在无向图中,若任意两个顶点之间都存在边,那么称这个图为无向完全图。
- 有向完全图:在有向图中,若任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。
- 其他:还有一些诸如稀疏图、稠密图、简单图,网等概念,用的不多就不一一详述了。有需要的可以参考《大话数据结构》图章节的相关内容。
3、图中顶点和边的关系
(1)在无向图中:
- 度:某一个顶点的度表示的是与该顶点相连的边的数量。通过对于一些实例的分析我们可以得到无向图中度的数目等于边的数目的两倍 的恒等关系。
(2)在有向图中:
- 对应的在有向图中度的概念可以细分为入度和出度。通过实例计算可以知道:入度等于出度。
- 入度:顶点为弧头的顶点的数目称为入度。
- 出度:顶点为弧尾的顶点的数目称为出度。
4、连通图相关术语
- 环:图中两顶点之间存在可以相互到达的路径说明是连通的,如果路径最终回到起始点则称为环;
- 连通图:若任意两个顶点都是连通的,则图就是连通图(无向图中这样称呼),有向图中则称为强连通图。
- 连通分量:图中有子图,若子图极大连通则就是连通分量(无向图中这样称呼),有向图中的则称为强连通分量。
二、一个题目
看到这里,想必图论的基本术语已经都了解清楚了,现在让我们通过一个例子来看一个如何建图。
1、题目描述
给你一个 m x n 的网格图 grid 。 grid 中每个格子都有一个数字,对应着从该格子出发下一步走的方向。 grid[i][j] 中的数字可能为以下几种情况:
- 1 ,下一步往右走,也就是你会从 grid[i][j] \texttt{grid[i][j]} grid[i][j] 走到 grid[i][j + 1] \texttt{grid[i][j + 1]} grid[i][j + 1]
- 2 ,下一步往左走,也就是你会从 grid[i][j] \texttt{grid[i][j]} grid[i][j] 走到 grid[i][j - 1] \texttt{grid[i][j - 1]} grid[i][j - 1]
- 3 ,下一步往下走,也就是你会从 grid[i][j] \texttt{grid[i][j]} grid[i][j] 走到 grid[i + 1][j] \texttt{grid[i + 1][j]} grid[i + 1][j]
- 4 ,下一步往上走,也就是你会从 grid[i][j] \texttt{grid[i][j]} grid[i][j] 走到 grid[i - 1][j] \texttt{grid[i - 1][j]} grid[i - 1][j]
注意网格图中可能会有 无效数字 ,因为它们可能指向 grid \texttt{grid} grid 以外的区域。
一开始,你会从最左上角的格子 (0,0) \texttt{(0,0)} (0,0) 出发。我们定义一条 有效路径 为从格子 (0,0) \texttt{(0,0)} (0,0) 出发,每一步都顺着数字对应方向走,最终在最右下角的格子 (m - 1, n - 1) \texttt{(m - 1, n - 1)} (m - 1, n - 1) 结束的路径。有效路径 不需要是最短路径 。
你可以花费 cost = 1 \texttt{cost = 1} cost = 1 的代价修改一个格子中的数字,但每个格子中的数字 只能修改一次 。
请你返回让网格图至少有一条有效路径的最小代价。
2、题目分析
(1)建图,如何建图呢?建立当前网格与可以到达的网格之间的图,权值为0;无法到达的网格权值为1,因为无法到达所以需要 花费1个单位到达;
(2)建图需要建立的是两个顶点之间的权值关系,因此需要把格子上的每个二维点映射成建图需要的一维点;
(3)最后题目就转化为求从
(0,
0)
\texttt{(0, 0)}
(0, 0) 到
(n-1,
m-1)
\texttt{(n-1, m-1)}
(n-1, m-1) 的最短花费也就是最短路径
O
K
OK
OK 了。
3、算法实现与解释
class Solution {
#define manx 10000
struct Edges{ // (1)
int v, w;
Edges(){};
Edges(int _v, int _w) : v(_v), w(_w){}
};
vector<Edges> edges[manx];
vector<vector<int>> dirs = { // (2)
{-1, -1},
{0, 1},
{0, -1},
{1, 0},
{-1, 0}
};
int getNode(int i, int j){ // (3)
return i * 100 + j;
}
int bfs(int start, int end){ // (4)
queue<int> q;
int dist[manx];
memset(dist, -1, sizeof(dist));
q.push(start);
dist[start] = 0;
while(!q.empty()){
int start = q.front();
q.pop();
for(int i = edges[start].size()-1; i >= 0; --i){
int v = edges[start][i].v;
int w = dist[start] + edges[start][i].w;
if(dist[v] == -1 || w < dist[v]){
dist[v] = w;
q.push(v);
}
}
}
return dist[end];
}
public:
int minCost(vector<vector<int>>& grid) {
int i, j, k;
int n = grid.size();
int m = grid[0].size();
int nm = n * m;
for(i = 0; i < nm; ++i){
edges[i].clear();
}
for(i = 0; i < n; ++i){ // (5)
for(j = 0; j < m; ++j){
for(k = 1; k <= 4; ++k){
int w = (grid[i][j] == k) ? 0 : 1;
int x = i + dirs[k][0];
int y = j + dirs[k][1];
if(x < 0 || x >= n || y < 0 || y >= m){
continue;
}
int u = getNode(i, j);
int v = getNode(x, y);
edges[u].push_back(Edges(v, w));
}
}
}
return bfs(getNode(0, 0), getNode(n-1, m-1));
}
};
(
1
)
(1)
(1)定义边权结构体;
(
2
)
(2)
(2)根据题目定义右、左、下、上四个方向,注意要与
1、2、3、4
\texttt{1、2、3、4}
1、2、3、4 相对应;
(
3
)
(3)
(3)二维格点映射到到一维顶点
(
4
)
(4)
(4)Dikstra算法的堆优化;
(
5
)
(5)
(5)根据分析建边的过程。
三、建图详解
通过 这个例题 我们知道了建图的必要性,现在开始介绍几种我常使用的建图方法。
1、邻接矩阵的方法
直接给了一个标有顶点和边的图,或者一个定义边权的二维数组,用邻接矩阵来存储边权结构,方便后续计算。比如图三。
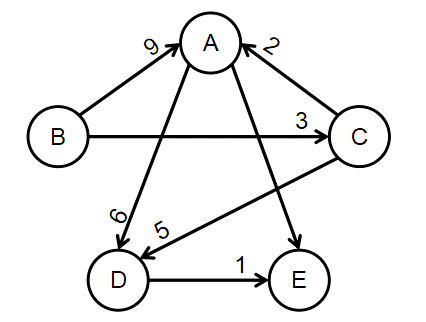
图3 带权有向图
|
int vertex = [A, B, C, D, E] // 顶点数组
int edges[][] = { // 有向边数组
{0, INF, INF, INF, 6},
{9, 0, 3, INF, INF},
{2, INF, 0, 5, INF},
{INF, INF, INF, 0, 1},
{INF, INF, INF, INF, 0},
}
// 读取边与权重
// 直接索引就好
edges[0][4]; // 读取的就是顶点A到顶点E的有向权值
2、边权图结构体
例题中使用的建立边权的方法,也是比较常用的方法
struct Edge{
int v;
int w;
Edge() {};
Edge(int _v, int _w) : v(_v), w(_w){};
};
vector<Edge> edges[110];
// u——v w
edges[u].push_back(Edge<v, w>);
3、总结
不论是使用邻接矩阵还是使用结构体建图,都可以,只要可以清晰明了地从自己的边权图中读取相应的边权值以及加入新的边权就可以。选自己比较熟悉的方法,这里还是推荐使用 结构体 的方法,一方面可以加强对结构体的理解,另一方面这种方法用的多。
建图还有一种就是建立反图,其实本质也就是建图。只是将有向图中建立弧尾到弧头的图,反向建立为弧头到弧尾的图。这一点在 拓扑排序 中会详述。
四、相关习题
| 题号 | 难度 |
|---|---|
| 802. 找到最终的安全状态 | Medium |
| 剑指 Offer II 108. 单词演变 | Hard |
| 1368. 使网格图至少有一条有效路径的最小代价 | Hard |























 550
550











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










