ML1-回归模型

1. Linear Regression

• 核心思想：线性回归，通过属性的线性组合来拟合一条直线、平面或者超平面 $f(x_i)=w{x}_i+b$，使得真实值与预测值之间的均方误差最小。
• 损失函数：平方损失 $L(y,f(x_i))=(y-f(x_i){)}^2$
• 目标函数：${\hat{w}}^{\ast }=\underset{\hat{w}}{argmin}(y-X\hat{w}{)}^T(y-X\hat{w})$
  $$y-X\hat{w}=\left(\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right)-\left(\begin{array}{ccccc}{x}_{11}& x_{12}& ...& x_{1d}& 1\\ x_{21}& x_{22}& ...& x_{2d}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ x_{m1}& x_{m2}& ...& x_{md}& 1\end{array}\right)\left(\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_d\\ b\end{array}\right)$$ $$其中，d:特征维度，m:样本数量，\hat{w}:权重参数，b:偏置$$
• 求解方法：
  • 最小二乘法：
    • 第一步：令经验风险 $E_{\hat{w}}=(y-X\hat{w}{)}^T(y-X\hat{w})$，则$$E_{\hat{w}}=y^{T}y-y^{T}X\hat{w}-{\hat{w}}^T{X}^{T}y+{\hat{w}}^T{X}^{T}X\hat{w}$$
    • 第二步：当矩阵$X^{T}X$为满秩矩阵或正定矩阵时，另导数$\frac{\partial E_{\hat{w}}}{\partial \hat{w}}=0$，得到解析解 ${\hat{w}}^{\ast }=(X^{T}X{)}^{-1}{X}^{T}y$
    • 第三步：当矩阵$X^{T}X$不满秩时（属性数量大于样本数），需要利用奇异值分解-SVD求逆矩阵$(X^{T}X{)}^{-1}$，进而求得${\hat{w}}^{\ast }$。此时，存在多个解。
  • 梯度下降法：$GradientDescent$，迭代更新 $w_{i+1}=w_i-\alpha \frac{\partial E_{\hat{w}}}{\partial \hat{w}}$
• 优点：权重参数直观表达了属性的重要程度，可解释性好。

2. Lasso Regression

• 核心思想：Least Absolute Shrinkage and Selection Operator （最小绝对值收敛和选择算子）。线性回归+$L_1$正则化项。
• 目标函数：${\hat{w}}^{\ast }=\underset{\hat{w}}{argmin}(y-X\hat{w}{)}^T(y-X\hat{w})+\lambda ||\hat{w}|{|}_1$

3. Ridge Regression

• 核心思想：岭回归，线性回归+$L_2$正则化项。
• 目标函数：${\hat{w}}^{\ast }=\underset{\hat{w}}{argmin}(y-X\hat{w}{)}^T(y-X\hat{w})+\lambda ||w|{|}_2^2$

4. ElasticNet Regression

• 核心思想：弹性网络，线性回归 + $L_1$正则化项 + $L_2$正则化项
• 目标函数：${\hat{w}}^{\ast }=\underset{\hat{w}}{argmin}(y-X\hat{w}{)}^T(y-X\hat{w})+\lambda (\alpha ||w|{|}_1+(1-\alpha )||w|{|}_2^2)$

5. Ridge VS LASSO

• 稀疏解：LASSO 回归的平方误差等值线 与 $L_1$正则化项等值线交点更容易出现在坐标轴上，即$w_1$或$w_2$为0；Ridge 回归的平方误差等值线 与 $L_2$正则化项等值线交点更容易出现在坐标系中。因此，LASSO 回归 比 Ridge 回归更容易得到稀疏解。LASSO可以进行 feature selection，而 Ridge不行。

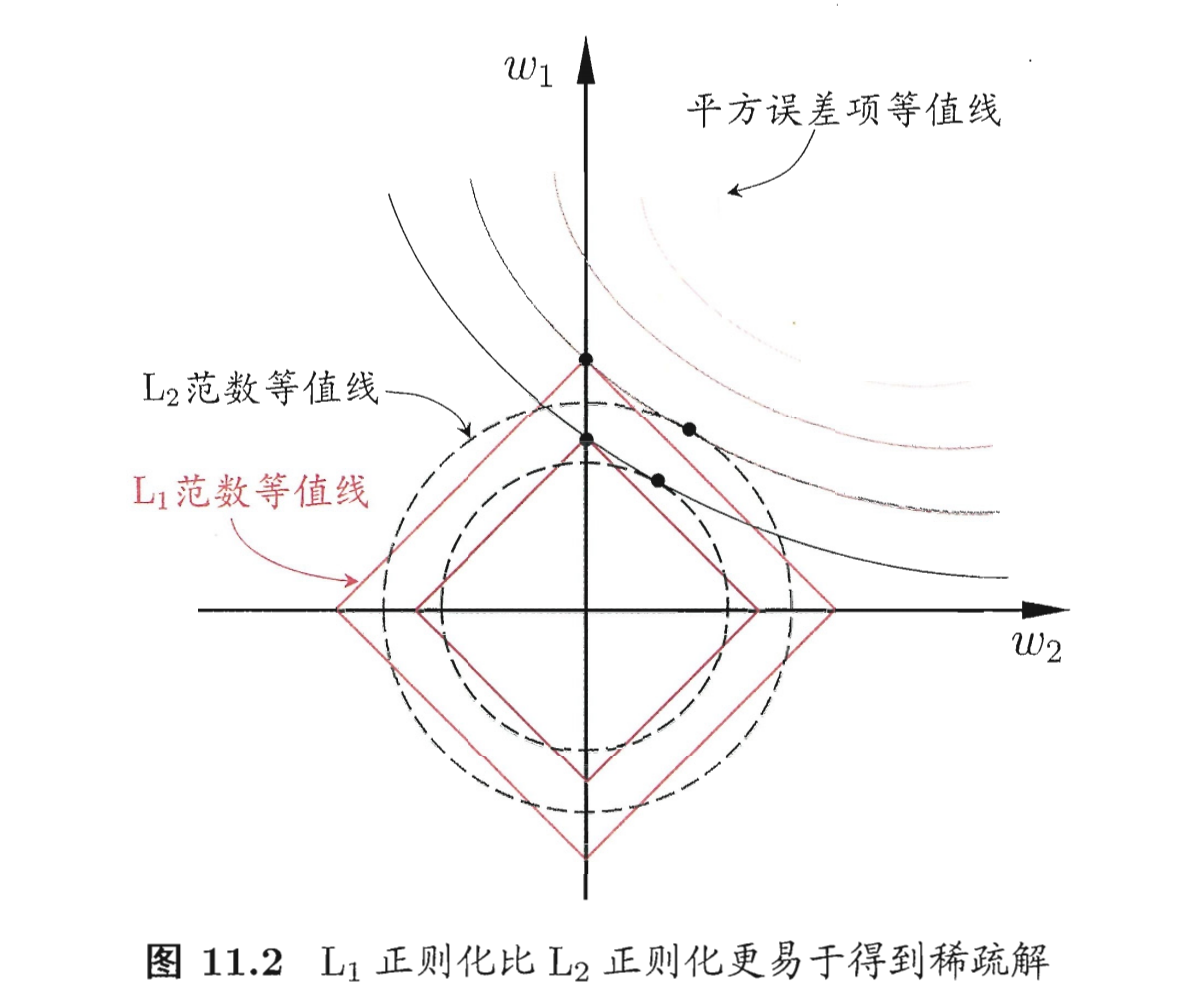
• 从贝叶斯角度看，L1 正则等价于参数 𝑤 的先验概率分布满足拉普拉斯分布，而 L2 正则等价于参数 𝑤 的先验概率分布满足高斯分布。