【学习笔记】第四章概率论与数理统计

Burger叮当

已于 2022-02-10 19:49:31 修改

阅读量2.1k

点赞数 2

分类专栏：司守奎老师 python数学建模文章标签：概率论机器学习人工智能

于 2022-01-24 22:58:40 首次发布

本文链接：https://blog.csdn.net/weixin_54581900/article/details/122675334

版权

4.3.2 参数假设检验（知道总体服从什么类型的分布）

1. 单个总体均值的假设检验

4.3.3 非参数假设检验（不知道总体服从什么类型的分布）

1. 分布拟合检验（检验法）

2. Kolmogorov-Smirnov检验

4.4 方差分析

4.4.1 单因素方差分析及python实现

4.4.2 双因素方差分析及python实现

1. 数学模型

4.1 随机变量的概率计算和数字特征

4.1.1 随机变量的概率计算

例4.1 设 $X\sim N(3,5^2)$ (1）求P{2<X<6}；（2）确定c，使P{-3c<X<2c}=0.6

from scipy.stats import norm
from scipy.optimize import fsolve
print("p=",norm.cdf(6,3,5)-norm.cdf(2,3,5))#做差，后减前
f=lambda c: norm.cdf(2*c,3,5)-norm.cdf(-3*c,3,5)-0.6
print("c=",fsolve(f,0))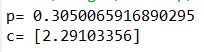

定义4.1 α分位数

若连续型随机变量X的分布函数为 $F(x)$ ,对于0<α<1,若 $x_\alpha$ 使得 $P\left \{ X\leq x_\alpha \right \}=\alpha$ ,则称 $x_\alpha$ 为这个分布的α分位数。若 $F(x)$ 的反函数 $F^{-1}(x)$ 存在,则有 $x_\alpha =F^{-1}(1-\alpha )$

定义4.2 上α分位数

若连续型随机变量X的分布函数为 $F(x)$ ，对于 $0<\alpha <1$ ,若 $\tilde{x}_\alpha$ 使得 $P\left \{ X>\tilde{x}_\alpha \right \}=\alpha$ ，则称 $\tilde{x}_\alpha$ 为这个分布的上α分位数。 若 $F(x)$ 的反函数 $F^{-1}(x)$ 存在,则有 $\tilde{x}_\alpha =F^{-1}(1-\alpha )$

例4.2 设 $X\sim N(0,1)$ ,若 $z_\alpha$ 满足条件 $P\left \{X > z_\alpha \right \}= \alpha ,0<\alpha <1$ ，则称 $z_\alpha$ 为标准正态分布的上α分位数。试计算几个常用的 $z_\alpha$ 的值,并画出 $z_{0.1}$ 的示意图.
计算得到几个常用的 $z_\alpha$ 的值见下表， $z_{0.1}$ 的示意图见下图：

from scipy.stats import norm
from pylab import plot,fill_between,show,text,savefig,rc 
from numpy import array, linspace, zeros
alpha=array([0.001, 0.005, 0.01, 0.025, 0.05, 0.10])#表中给的alpha的值
za=norm.ppf(1-alpha,0,1)  #求上alpha分位数  #定义4.2
print("上alpha分位数分别为", za)
x=linspace(-4, 4, 100); y=norm.pdf(x, 0, 1)
rc('font',size=16); rc('text',usetex=True)
plot(x,y)  #画标准正态分布密度曲线
x2=linspace(za[-1],4,100)#在0.1对应的上alpha分位数和4之间取100个点
y2=norm.pdf(x2);
y1=[0]*len(x2)
fill_between(x2, y1, y2, color='r')  #y1,y2对应的点之间填充
plot([-4,4],[0,0])  #画水平线    # [-4,0]|[4,0]
text(1.9, 0.07, "$\\leftarrow\\alpha$=0.1")  #标注
savefig("figure4_2.png", dpi=500); show()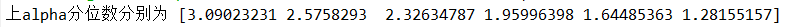

4.1.2 随机变量数字特征简介

定义4.3：设随机变量X的分布律为： $P\left \{ X=x_k \right \}=p_k,k=1,2,\cdots ,$

若级数 $\sum_{k=1}^{\infty }x_kp_k$ 绝对收敛，则称级数 $\sum_{k=1}^{\infty }x_kp_k$ 的和为随机变量X的数学期望，记为 $E(X)$ ,即 $E(X)=\sum_{k=1}^{\infty }x_kp_k$

定义4.4：设X是一个随机变量，若 $E\left \{ [X-E(X)]^2 \right \}$ 存在，则称 $E\left \{ [X-E(X)]^2 \right \}$ 为X的方差，记为D(X)或Var(X)，即：

$D(X)=Var(X)=E\left \{ [X-E(X)]^2 \right \}$

$\sigma (x)=\sqrt{D(X)}$ 称为标准差或均方差。

方差其实就是随机变量X的函数 $g(X)= [X-E(X)]^2$ 的数学期望

定义4.5：随机变量X的偏度和峰度指的是X的标准化变量 $(X-E(X))/\sqrt{D(X)}$ 的三阶中心距和四阶中心矩：

$v_1=E[(\frac{X-E(x)}{\sqrt{D(X)}})^3]=\frac{E[(X-E(X))^3]}{(D(X))^2}$

$v_2=E[(\frac{X-E(x)}{\sqrt{D(X)}})^4]=\frac{E[(X-E(X))^4]}{(D(X))^2}$

定义4.6： $E\{[X-E(X)][Y-E(Y)]\}$ 称为随机变量X与Y的协方差，记为Cov(X,Y)，即

$Cov(X,Y)=E\{[X-E(X)][Y-E(Y)]\}$

而 $\rho_{XY}=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$ 称为随机变量X与Y的相关系数。、

定义4.7：k阶矩，中心矩，混合矩，混合中心矩

最低0.47元/天解锁文章

Burger叮当

关注

2
点赞
踩
16

收藏

觉得还不错? 一键收藏
0
评论
【学习笔记】第四章概率论与数理统计

4.1 随机变量的概率计算和数字特征4.1.1 随机变量的概率计算例4.1 设 (1）求P{2<X<6}；（2）确定c，使P{-3c<X<2c}=0.6from scipy.stats import normfrom scipy.optimize import fsolveprint("p=",norm.cdf(6,3,5)-norm.cdf(2,3,5))#做差，后减前f=lambda c: norm.cdf(2*c,3,5)-norm.cdf(-3*c,3,
复制链接

扫一扫