前言
由于学习需要对这一部分的内容进行了简单了解,在社区里也有很多人写了相关的内容,我想记录自己在学习过程中的收获或者说问题,计划来写这篇博客,打算通过三部分来结束稀疏性和压缩感知的内容,参考的书目为数据驱动的科学和工程,当然B站上提供了这本书的讲解,链接如下数据驱动的科学和工程,在评论区中给出了此书的PDF,书中的代码链接如下代码,当然我也会在文中给出并且适当注释,文中就用Python来说明。
1、稀疏性和压缩
所谓稀疏性就是向量、矩阵等中的项大多数为0或者非常接近0,大多数的信号都是高度可压缩的,压缩信号
X
∈
R
n
X\in{R}^{n}
X∈Rn基于变换基
Ψ
∈
R
n
×
n
\Psi\in{R}^{n\times n}
Ψ∈Rn×n能够写成一个稀疏向量
s
∈
R
n
s\in{R}^{n}
s∈Rn:
x
=
Ψ
s
\mathbf{x}=\Psi\mathbf{s}
x=Ψs,如果
s
s
s中有
K
K
K个非零元素,则称为
K
K
K稀疏的。如果基底
Ψ
\Psi
Ψ是通用的,比如傅里叶或者小波基,则仅需要
s
s
s中的非零项即可重构原始信号。
下面是一个基于傅里叶变换的图像压缩,主要思路是使用快速傅里叶变换在对数坐标系上绘制系数,按大小排列后决定保留百分比,或者称为设置截断阈值,最后通过逆FFT绘制压缩后的图像:
from matplotlib.image import imread
import numpy as np
import matplotlib.pyplot as plt
import os
from mpl_toolkits.mplot3d import Axes3D
plt.rcParams['figure.figsize'] = [12, 8]# 图像显示大小
plt.rcParams.update({'font.size': 18})#字体大小
#彩色图片一般是由RGB组成,其实就是3个二维数组叠加而成,当R=G=B时,彩色图片就会变成一种灰度颜色,所以灰度颜色的图片其实就是一个二维数组
#灰度化处理总共有三种方法:最大值法、平均值法、加权平均法
A = imread(os.path.join('..','DATA','jelly.jpg'))
Abw = np.mean(A, -1); # 转化为灰度图像也可以通过cv2库或者plt,
#0:压缩行,对各列求均值,返回 1* n 矩阵,axis =1 :压缩列,对各行求均值,返回 m *1 矩阵
plt.imshow(Abw,cmap='gray')# cmap将标量数据映射到色彩图
plt.axis('off')#设置坐标轴(关闭)
plt.show()
## Compute FFT of image using fft2
At = np.fft.fft2(Abw)#计算二维的傅里叶变换(收藏图像傅里叶变换原理 python实现)
F = np.log(np.abs(np.fft.fftshift(At))+1) # 将图像中的低频部分移动到图像的中心;将 FFT 置于对数刻度上
plt.imshow(F,cmap='gray')
plt.axis('off')
plt.show()
## Zero out all small coefficients and inverse transform
Bt = np.sort(np.abs(np.reshape(At,-1)))#重组排序(由小到大)
keep = 0.05
thresh = Bt[int(np.floor((1-keep)*len(Bt)))]#取出截断的傅里叶系数
ind = np.abs(At) > thresh#大于取1,小于取0
Atlow = At * ind#保留截断后的系数,其他变为0
Flow = np.log(np.abs(np.fft.fftshift(Atlow))+1)
plt.imshow(Flow,cmap='gray')
plt.axis('off')
plt.show()
## 逆FFT绘制压缩后的图像
Alow = np.fft.ifft2(Atlow).astype('uint8')
plt.imshow(Alow,cmap='gray')
plt.axis('off')
plt.show()
plt.rcParams['figure.figsize'] = [16, 8]
fig = plt.figure()
ax1 = fig.add_subplot(1, 2, 1, projection='3d')
ax2 = fig.add_subplot(1, 2, 2, projection='3d')
Anew = Abw[::5,::5]
y = np.arange(Anew.shape[0])
x = np.arange(Anew.shape[1])
X,Y = np.meshgrid(x,y)
surf1 = ax1.plot_surface(X,Y,Anew, rstride=1, cstride=1,cmap='jet',#ax.plot_surface(X, Y, Z, alpha=1,rstride=1, cstride=1, cmap=parula_map)
linewidth=1, antialiased=False)
surf2 = ax2.plot_surface(X,Y,Anew, rstride=1, cstride=1,cmap='jet',
linewidth=1, antialiased=False)
#3D绘图之view_init()中的视角转换
ax1.view_init(90, 90) #(elev,azim)#改变绘制图像的视角,即相机的位置,azim沿着z轴旋转,elev沿着y轴
ax1.axis('off')
ax2.view_init(60, 90)
ax2.axis('off')
plt.show()
对于图像可压缩的原因也有必要说明,图像空间是广阔的,大多数维度都是冗余的(对于我们所关注的图像),如果我们找到了合适的变换基来识别,那么我们关注的图像是高度可压缩的。
2、压缩感知
从数学上来讲,压缩感知利用信号在通用基上的稀疏性,从极少的测量值中实现信号的完整重构,测量值
y
∈
R
p
y\in{R}^{p}
y∈Rp,
K
<
p
≪
n
K<p\ll n
K<p≪n:
y
=
C
X
y=CX
y=CX,其中
C
C
C表示测量矩阵。压缩感知的目标为求解满足以下方程的
s
s
s:
y
=
C
Ψ
s
=
Θ
s
y=C\Psi s=\Theta s
y=CΨs=Θs再利用
x
=
Ψ
s
\mathbf{x}=\Psi\mathbf{s}
x=Ψs重构
X
X
X,方程组是欠定的(行数小于列数,方程个数小于未知数个数)有无穷多组解。最稀疏的解
s
s
s满足一下优化问题:
s
^
=
a
r
g
m
i
n
s
∥
s
∥
0
s
u
b
j
e
c
t
t
o
y
=
C
Ψ
s
,
\hat{\mathrm{s}}=\underset{\mathrm{s}}{\mathrm{argmin}}\|\mathrm{s}\|_{0}\ \mathrm{subject~to} \ \ \mathrm{y}=\mathrm{C}\Psi\mathrm{s},
s^=sargmin∥s∥0 subject to y=CΨs,其中0范数表示非零项的个数(每一项的0次幂),它是凸函数(这个在这里介绍了三个范数函数的凹凸性)所以这个优化是非凸的,求解起来非常困难,只能通过穷举搜索求解,进而通过松弛手法放宽为:
s
^
=
a
r
g
m
i
n
s
∥
s
∥
1
s
u
b
j
e
c
t
t
o
y
=
C
Ψ
s
,
\hat{\mathrm{s}}=\underset{\mathrm{s}}{\mathrm{argmin}}\|\mathrm{s}\|_{1}\ \mathrm{subject~to} \ \ \mathrm{y}=\mathrm{C}\Psi\mathrm{s},
s^=sargmin∥s∥1 subject to y=CΨs,
但是需要满足某些条件才能使1范数的解收敛到0范数的解:
1、测量矩阵
C
C
C的行与
Ψ
\Psi
Ψ的列不相关;
2、测量值
p
p
p必须足够大,大约:
p
≈
O
(
K
log
(
n
/
K
)
)
≈
k
1
K
log
(
n
/
K
)
.
p\approx\mathcal{O}(K\log(n/K))\approx k_1K\log(n/K).
p≈O(Klog(n/K))≈k1Klog(n/K).其中
k
1
k_1
k1取决于1中的非相关程度。
这两个条件保证了
C
Ψ
C \Psi
CΨ对系数向量
s
s
s是一个酉变换(保内积)。 压缩感知与直觉相悖,香农奈奎斯特采样定理说明信号的准确恢复需要以最高频率的两倍的速率采样,不过压缩感知一方面依赖于低采样率下得随机采样,另一方面依赖于精确地采样时间。
当测量值
y
y
y中含有噪声时,上述两式可以变形为
s
^
=
a
r
g
m
i
n
s
∥
s
∥
1
,
s
u
b
j
e
c
t
t
o
∥
C
Ψ
s
−
y
∥
2
<
ε
.
\hat{\mathbf{s}}=\underset{s}{\mathrm{argmin}}\|\mathbf{s}\|_{1},\mathrm{subject~to}\|\mathbf{C}\mathbf{\Psi}\mathbf{s}-\mathbf{y}\|_{2}<\varepsilon.
s^=sargmin∥s∥1,subject to∥CΨs−y∥2<ε.相关的凸优化为
s
^
=
a
r
g
m
i
n
s
∥
C
Ψ
s
−
y
∥
2
+
λ
∥
s
∥
1
.
\hat{\mathbf{s}}=\underset{s}{\mathrm{argmin}}\|\mathbf{C}\Psi\mathbf{s}-\mathbf{y}\|_2+\lambda\|\mathbf{s}\|_1.
s^=sargmin∥CΨs−y∥2+λ∥s∥1.其中
λ
\lambda
λ大于等于0是衡量稀疏性重要程度的加权参数。
3、压缩感知示例
这一节探讨压缩感知用于系数信号恢复的具体示例,第一个例子为求解通用欠定方程组,
l
1
l_1
l1范数会促进稀疏性;第二个例子为稀疏双音音频信号的恢复。
例1:建立一个
y
=
Θ
s
y=\Theta s
y=Θs的矩阵方程组,
y
y
y为
p
=
200
p=200
p=200的列向量,
n
=
1000
n=1000
n=1000,
Θ
\Theta
Θ为
200
×
1000
200×1000
200×1000的矩阵,
s
s
s为1000维的列向量,我们的目标是求解最小
l
1
、
l
2
l_1、l_2
l1、l2范数解,对应第二节中的优化问题,具体代码如下:
import numpy as np
import matplotlib.pyplot as plt
import os
from scipy.optimize import minimize
plt.rcParams['figure.figsize'] = [12, 18]
plt.rcParams.update({'font.size': 18})
# Solve y = Theta * s for "s"
n = 1000 # dimension of s
p = 200 # number of measurements, dim(y)
Theta = np.random.randn(p,n)#返回一个或一组服从标准正态分布的随机样本值。
y = np.random.randn(p)
# L1 Minimum norm solution s_L1
def L1_norm(x):
return np.linalg.norm(x,ord=1)#定义函数返回1范数linalg=linear+algebra
constr = ({'type': 'eq', 'fun': lambda x: Theta @ x - y})#lambda定义匿名函数,eq为等式条件
x0 = np.linalg.pinv(Theta) @ y # initialize with L2 solution
res = minimize(L1_norm, x0, method='SLSQP',constraints=constr)
s_L1 = res.x
# L2 Minimum norm solution s_L2
s_L2 = np.linalg.pinv(Theta) @ y
fig,axs = plt.subplots(2,2)#subplots()方法一次性创建2x2布局的四个Axes对象
axs = axs.reshape(-1)
axs[0].plot(s_L1,color='b',linewidth=1.5)
axs[0].set_ylim(-0.2,0.2)
axs[1].plot(s_L2,color='r',linewidth=1.5)
axs[1].set_ylim(-0.2,0.2)
axs[2].hist(s_L1,bins=np.arange(-0.105,0.105,0.01),rwidth=0.9)#hist直方图
axs[3].hist(s_L2,bins=np.arange(-0.105,0.105,0.01),rwidth=0.9)
plt.show()
其中
l
1
l_1
l1范数由min函数求出,
l
2
l_2
l2范数由
Θ
\Theta
Θ的伪逆求解,得到两个稀疏向量和它的直方图如下:(左为1范数,右为2范数)
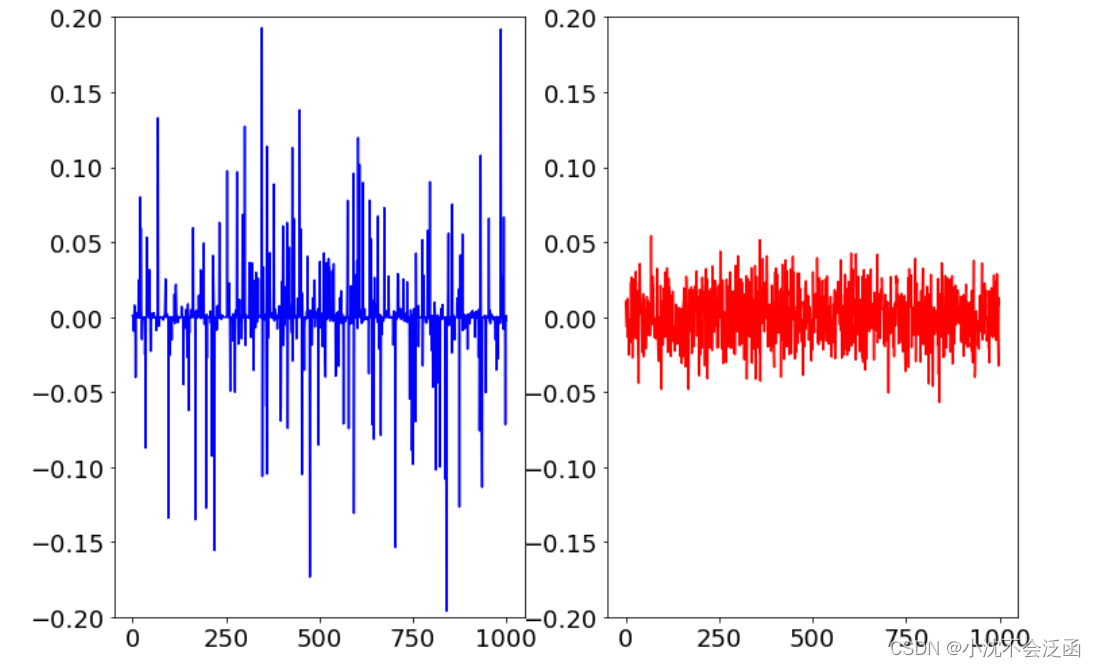
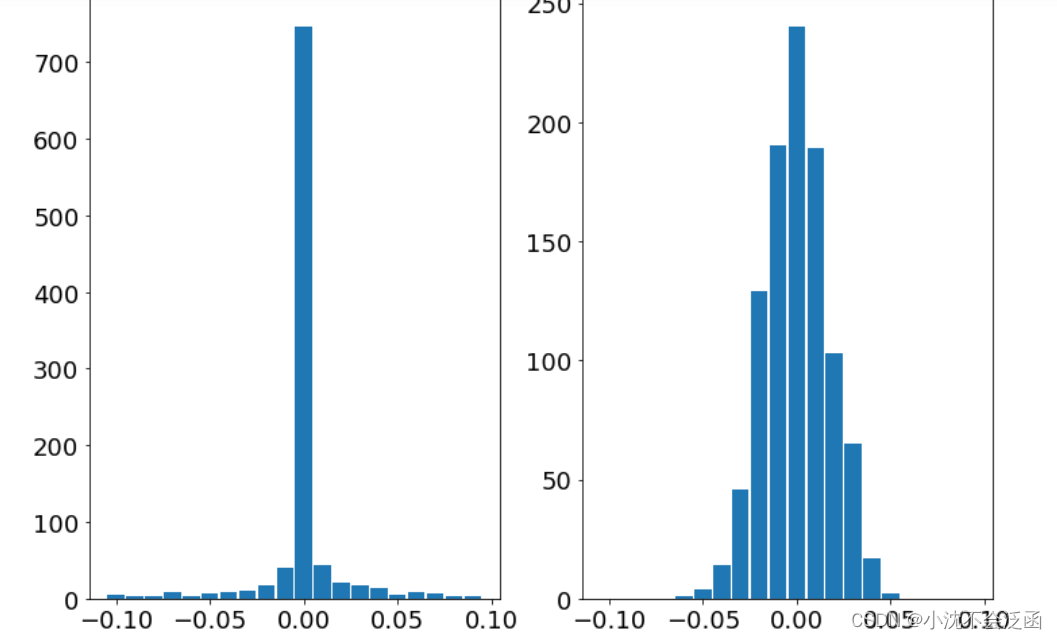
由图可知1范数的确是稀疏的,并且非零项的个数与测量值的个数相对应,而2范数的结果类似于正态分布。对于各种范数的几何特征如图:
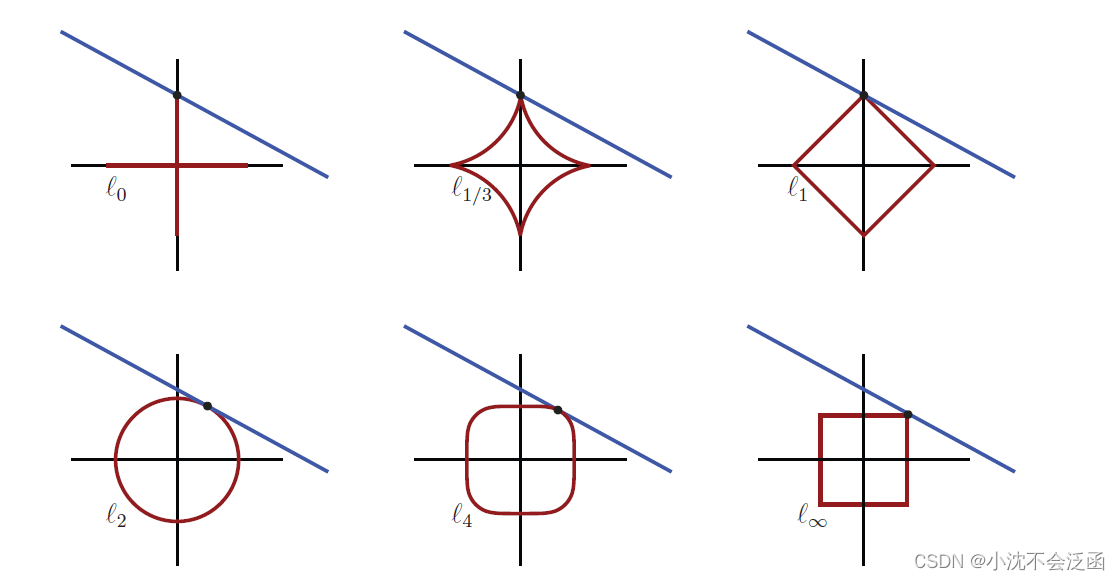
不妨假定在二维空间中,蓝色的线表示各范数的稀疏解,棕色的代表各范数等于某一值,在它们的交点处可知
l
0
,
l
1
/
3
,
l
1
l_0,l_{1/3},l_1
l0,l1/3,l1范数的其中一个坐标为0,因而稀疏。
例2:为了说明压缩感知从一组稀疏的随机测量集中重构高维信号,考虑由两股余弦波组成的信号:
x
(
t
)
=
cos
(
2
π
×
97
t
)
+
cos
(
2
π
×
777
t
)
.
x(t)=\cos(2\pi\times97t)+\cos(2\pi\times777t).
x(t)=cos(2π×97t)+cos(2π×777t).该信号在频域的振幅谱中是稀疏的,最高频率为777HZ,因此奈奎斯特采样理论的采样率为1554HZ,这些随机采样的平均采样率为128HZ,远远低于奈奎斯特采样率。完整信号从
t
=
0
t=0
t=0到
t
=
1
t=1
t=1生成,分辨率
n
=
4096
n=4096
n=4096,在
p
=
128
p=128
p=128个时间点随机采样,具体代码如下(在python中需要定义匹配追踪函数):
import numpy as np
import matplotlib.pyplot as plt
import os
import sys
from scipy.fftpack import dct, idct
from scipy.optimize import minimize
sys.path.append(os.path.join('..','UTILS'))
#from cosamp_fn import cosamp
# cosamp function is available at https://github.com/avirmaux/CoSaMP
# copy function from ipynb into cosamp_fn.py and place in UTILS folder
plt.rcParams['figure.figsize'] = [12, 12]
plt.rcParams.update({'font.size': 18})
#定义匹配追踪函数cosamp
def cosamp(phi, u, s, epsilon=1e-10, max_iter=1000):
"""
Return an `s`-sparse approximation of the target signal
Input:
- phi, sampling matrix
- u, noisy sample vector
- s, sparsity
"""
a = np.zeros(phi.shape[1])
v = u
it = 0 # count
halt = False
while not halt:
it += 1
print("Iteration {}\r".format(it), end="")
y = np.dot(np.transpose(phi), v)
omega = np.argsort(y)[-(2*s):] # large components
omega = np.union1d(omega, a.nonzero()[0]) # use set instead?
phiT = phi[:, omega]
b = np.zeros(phi.shape[1])
# Solve Least Square
b[omega], _, _, _ = np.linalg.lstsq(phiT, u)
# Get new estimate
b[np.argsort(b)[:-s]] = 0
a = b
# Halt criterion
v_old = v
v = u - np.dot(phi, a)
halt = (np.linalg.norm(v - v_old) < epsilon) or \
np.linalg.norm(v) < epsilon or \
it > max_iter
return a
## Generate signal, DCT of signal
n = 4096 # points in high resolution signal
t = np.linspace(0,1,n)
x = np.cos(2 * 97 * np.pi * t) + np.cos(2 * 777 * np.pi * t)
xt = np.fft.fft(x) # Fourier transformed signal
PSD = xt * np.conj(xt) / n # Power spectral density
## Randomly sample signal
p = 128 # num. random samples, p = n/32
perm = np.floor(np.random.rand(p) * n).astype(int)
y = x[perm]#perm为128×1,x为1×4096,将Perm每个元素与x中的相乘求和得到1×128
## Solve compressed sensing problem
Psi = dct(np.identity(n)) # Build Psi
Theta = Psi[perm,:] #perm为128×1,psi为4096×4096,将Perm每个元素与psi中的每一列元素相乘求和得到128×4096
s = cosamp(Theta,y,10,epsilon=1.e-10,max_iter=10) # CS via matching pursuit
xrecon = idct(s) # reconstruct full signal
## Plot
time_window = np.array([1024,1280])/4096
freq = np.arange(n)
L = int(np.floor(n/2))
fig,axs = plt.subplots(2,2)
axs = axs.reshape(-1)
axs[1].plot(freq[:L],PSD[:L],color='k',linewidth=2)
axs[1].set_xlim(0, 1024)
axs[1].set_ylim(0, 1200)
axs[0].plot(t,x,color='k',linewidth=2)
axs[0].plot(perm/n,y,color='r',marker='x',linewidth=0,ms=12,mew=4)
axs[0].set_xlim(time_window[0],time_window[1])
axs[0].set_ylim(-2, 2)
axs[2].plot(t,xrecon,color='r',linewidth=2)
axs[2].set_xlim(time_window[0],time_window[1])
axs[2].set_ylim(-2, 2)
xtrecon = np.fft.fft(xrecon,n) # computes the (fast) discrete fourier transform
PSDrecon = xtrecon * np.conj(xtrecon)/n # Power spectrum (how much power in each freq)
axs[3].plot(freq[:L],PSDrecon[:L],color='r',linewidth=2)
axs[3].set_xlim(0, 1024)
axs[3].set_ylim(0, 1200)
plt.show()
重构出来的信号以及其功率谱密度如图
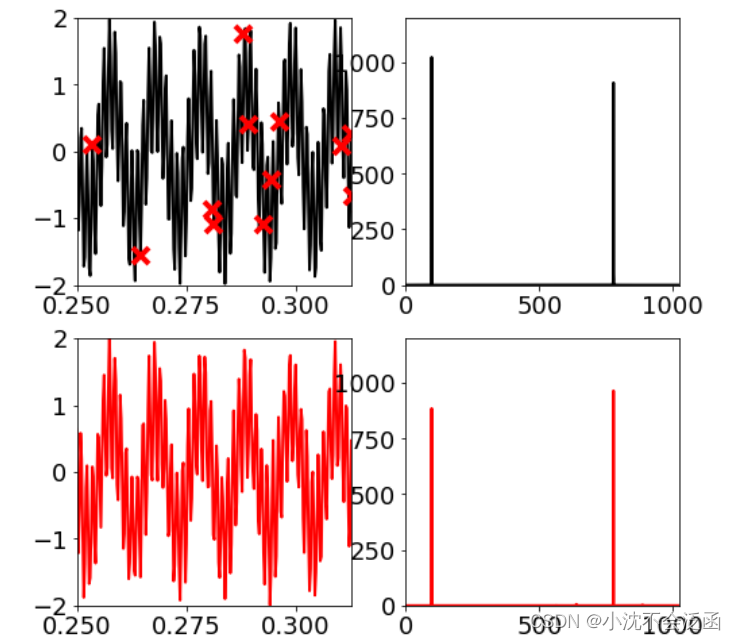
这里需要特别说明随机采样的重要性,如果均匀采样由奈奎斯特的理论显然失败,事实也的确如此,因为高频的信号可能被混叠,导致错误的峰值频率。这里我在MATLAB中进行了测试,均匀采样重构的结果如下:(python重构的结果太离谱了)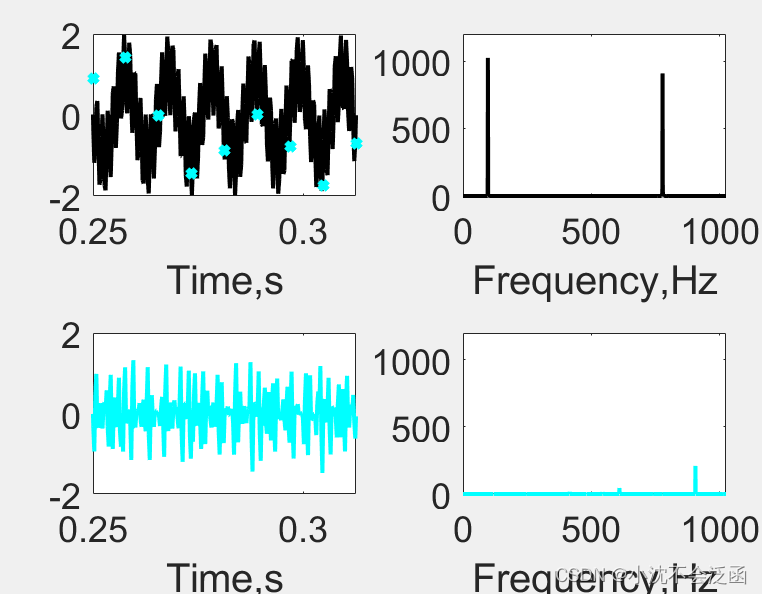
4、压缩几何
足够好的测量矩阵
C
C
C与
Ψ
\Psi
Ψ作用后将形成的矩阵
Θ
=
C
Ψ
\Theta =C \Psi
Θ=CΨ,它保留了稀疏向量
s
s
s的距离和内积结构,换句话说,我们要寻找一个测量矩阵,使得
Ψ
\Psi
Ψ作为稀疏向量上的一个近似等距映射,如果测量矩阵与稀疏基
Ψ
\Psi
Ψ的列非相干,意味着测量矩阵
C
C
C的行与
Ψ
\Psi
Ψ的列有很小的内积,如果测量矩阵与稀疏基的列相干,则测量矩阵将提供很少的信息。测量矩阵
C
C
C与基底
Ψ
\Psi
Ψ的非相干性由
μ
(
C
,
Ψ
)
\mu(\mathbf{C},\Psi)
μ(C,Ψ)给出:
μ
(
C
,
Ψ
)
=
n
max
j
,
k
∣
⟨
c
k
,
ψ
j
⟩
∣
\mu(\mathbf{C},\Psi)=\sqrt{n}\max_{j,k}|\langle\mathbf{c}_{k},\psi_{j}\rangle|
μ(C,Ψ)=nj,kmax∣⟨ck,ψj⟩∣其中
c
k
c_k
ck是测量矩阵
C
C
C的第
k
k
k行,
Ψ
j
\Psi_j
Ψj是矩阵
Ψ
\Psi
Ψ的第
j
j
j列。非相干系数
μ
\mu
μ的取值范围在1和
n
\sqrt{n}
n之间。如果非相干系数很小时,对于稀疏向量
s
s
s,矩阵
C
Ψ
C \Psi
CΨ满足受限等距性质(Restricted Isometry Property):
∣
∣
(
C
ψ
s
)
∣
2
2
∣
∣
S
∣
∣
2
2
−
1
∣
≤
δ
k
\left|\frac{\left|\left(C\psi s\right)\right|_{2}^{2}}{\left|\left|S\right|\right|_{2}^{2}}-1\right|\leq\delta_{k}
∣∣S∣∣22∣(Cψs)∣22−1
≤δk其中
δ
k
\delta_{k}
δk称为受限等距常数。当有足够多的测量值时,可以精确地确定稀疏向量中的
K
K
K个非零项,在这种情况下,常数
δ
k
\delta_{k}
δk存在一定的界限,由此保证对无噪声数据的精确信号重构。随机测量矩阵的示例很多,包括单像素随机、高斯随机、伯努利随机和稀疏随机等等:
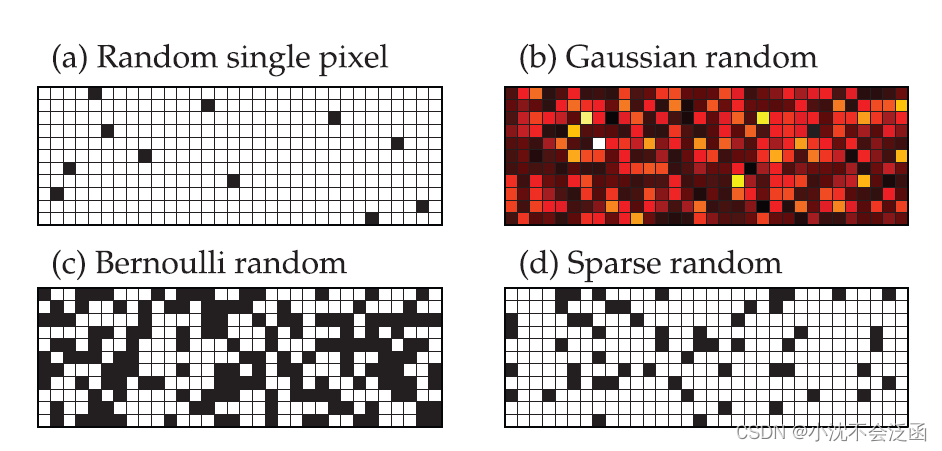
不好的测量矩阵会导致许多稀疏向量的重要信息丢失: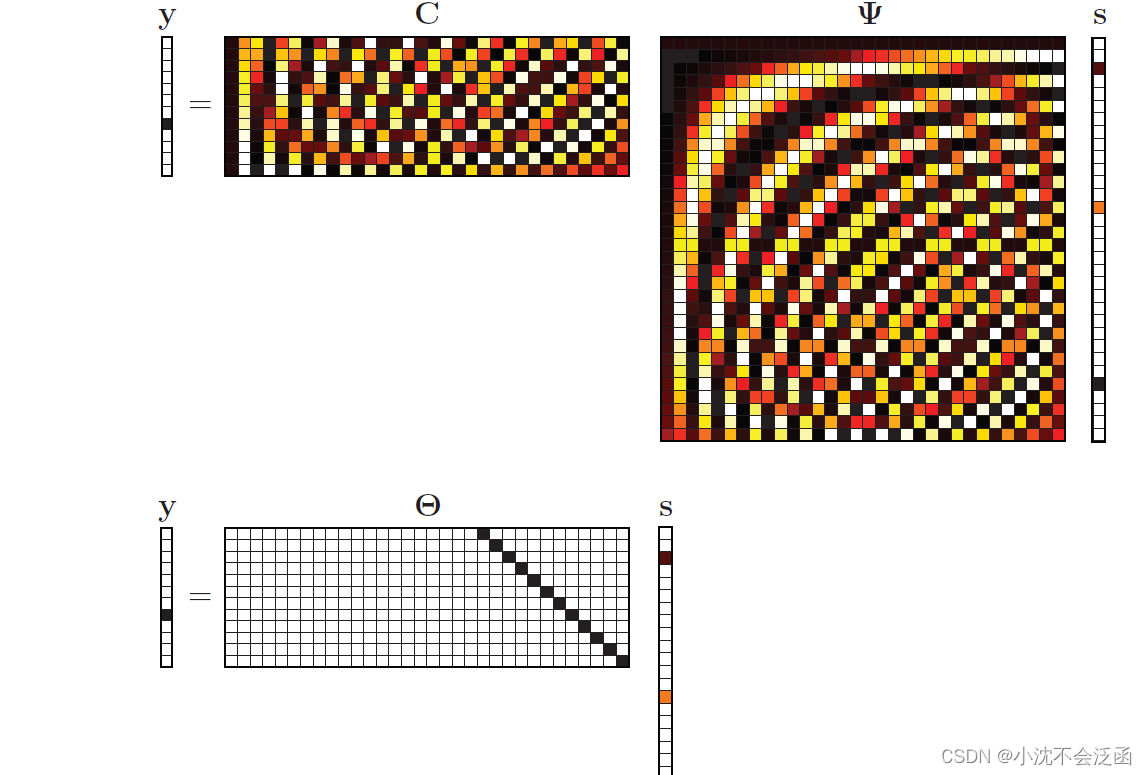





















 829
829











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










