奇异值分解（Singular Value Decomposition SVD）浅说

前言

这几天闲得实在无事，想做好多事但是一件也没做哈哈哈，今天抽出时间把前两天看的奇异值分解记录一下。

SVD概述

这个内容我相信很多人都听说过，在很多书中也当做基础知识或者基本内容来讲解，我之前也听过身边的同学讲过，涉及相关的知识也很多，比如主成分分析、本征正交分解、典型相关分析、快速傅里叶变换等等。
首先还是说一些中看不中用的废话吧啦啦啦，奇异值分解(SVD)是计算时代最为重耍的矩阵分解方式之、提供了一种数值稳定的矩阵分解结果，可用于多种应用目的并保证矩阵分解的存在性。我们将用SVD来获得矩阵的低秩近似，并对非方阵求取伪逆来找到方程组Ax=b的解。SVD的另个重要用途是作为主成分分析(PCA)的底层算法，可将高维数据分解为最具统计意义的描述因子，即降维，用少数变盘就能够反映原来众多变量的主要信息。SVD/PCA已广泛应用于理科和工科领域解决各种问题。SVD是一种从数据中提取这些模式的数值鲁棒和有效的方法。
所谓奇异值分解就是把矩阵分解为如下的形式：$X=U\Sigma V^{\mathrm{T}}$，例如$$\left[\begin{array}{cc}{x}_1& y_1\\ x_2& y_2\\ x_3& y_3\\ x_4& y_4\end{array}\right]=\left[\begin{array}{cccc}-& -& -& -\\ -& -& -& -\\ -& -& -& -\\ -& -& -& -\end{array}\right]\left[\begin{array}{cc}a& 0\\ 0& b\\ 0& 0\\ 0& 0\end{array}\right]\left[\begin{array}{cc}-& -\\ -& -\end{array}\right]$$
其中$U$和$V$都是正交矩阵或者酉矩阵，$\Sigma$为广义对角矩阵，包括$\left[\begin{array}{c}\hat{\Sigma }\\ 0\end{array}\right]\left[\begin{array}{c}\hat{\Sigma }0\end{array}\right]$两种，其中$\hat{\Sigma }$是对角矩阵，$M$是$n\times m$，当$n\ge m$时，$\Sigma$的对角线上最多有$m$个非零元素，则为第一种情况，反之是第二种，当然如果$M$是方阵则$\Sigma$就是对角矩阵。SVD可以分为全SVD(full SVD)和经济SVD(economy SCD)，其中经济SVD可以表示为：$\mathbf{X}=\mathbf{U\Sigma }{\mathbf{V}}^{\ast }=\left[\hat{\mathbf{U}}{\hat{\mathbf{U}}}^{\perp }\right]\left[\begin{array}{c}\hat{\Sigma }\\ 0\end{array}\right]{\mathbf{V}}^{\ast }=\hat{\mathbf{U}}\hat{\mathbf{\Sigma }}{\mathbf{V}}^{\ast }$，这里的$\Sigma$是第一种，$M$的行数大于列数，示意图如下：

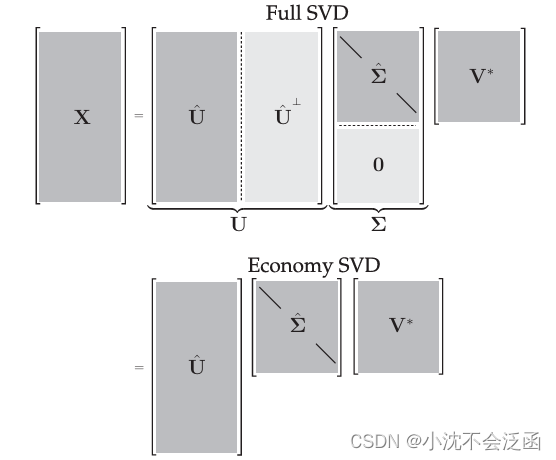
经济SVD保证了$\Sigma$是对角元素非零的对角矩阵，减少了运算中需要记录和储存的数据，或许是“经济”的内涵吧。$U$的列称为$X$的左奇异向量，$V$的列称为$X$的右奇异向量，$\hat{\Sigma }\in {\mathbb{C}}^{m\times m}$的对角线元素被称为奇异值，它们由大到小排列，$X$的秩等于非零奇异值的个数。

SVD计算与几何意义

$V$是$X^{\mathrm{T}}X$的特征向量；$U$是$X{X}^{\mathrm{T}}$的特征向量：$\Sigma$中的奇异值是$X^{\mathrm{T}}X$和$X{X}^{\mathrm{T}}$的特征值的算数平方根，二者的特征值相同。若将X视为一个线性变换，则酉矩阵$U、V$可以视为旋转变换，准对角矩阵$\Sigma$是伸缩变换，具体动画讲解可以看一下b站的视频：学长小课堂：什么是奇异值分解SVD–SVD如何分解时空矩阵对奇异值分解讲解的很清晰，后边的模态分解也很有意思，最重要的是动画制作不错。
书中也举了一个例子，简单来说明一下吧：由 S n − 1 = Δ { x ∣ ∥ x ∥ 2 = 1 } ⊂ R n S^{n-1}\stackrel{\Delta}{=}\{\mathbf{x}\mid\parallel\mathbf{x}\parallel_{2}=1\}\subset\mathbb{R}^{n} Sn−1=Δ{x∣∥x∥2​=1}⊂Rn确定的超球体通过$X$影射到由 { y ∣ y = X x , x ∈ S n − 1 } ⊂ R m \{\mathbf{y}\mid\mathbf{y}=\mathbf{X}\mathbf{x},\mathbf{x}\in S^{n-1}\}\subset\mathbb{R}^{m} {y∣y=Xx,x∈Sn−1}⊂Rm确定的椭球体，下图展示出了$R^3$中的一个球体和一个具有三个非零奇异值的映射$X$。因为通过$X$的映射(即矩阵乘法)是线性的，所以，知道了如何映射单位球体也就决定了所有其他向量是如何映射的。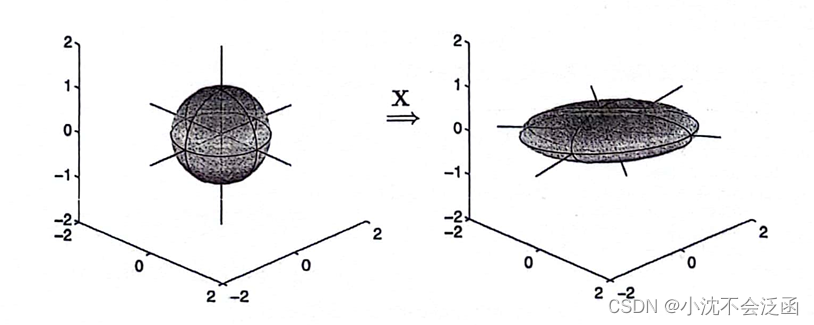
具体来说，利用三个旋转矩阵$R_x,R_y,R_z$来构造$X$，第四个矩阵用于拉伸和缩放主轴：
$$\begin{array}{c}\mathbf{X}=\underset{{\mathbf{R}}_{\mathbf{y}}}{\underbrace{\left[\begin{array}{ccc}\cos ({\theta }_3)& -\sin ({\theta }_3)& 0\\ \sin ({\theta }_3)& \cos ({\theta }_3)& 0\\ 0& 0& 1\end{array}\right]}}\underset{{\mathbf{R}}_{\mathbf{y}}}{\underbrace{\left[\begin{array}{ccc}\cos ({\theta }_2)& 0& \sin ({\theta }_2)\\ 0& 1& 0\\ -\sin ({\theta }_2)& 0& \cos ({\theta }_2)\end{array}\right]}}\\ \times \underset{{\mathbf{R}}_{\mathbf{x}}}{\underbrace{\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos ({\theta }_1)& -\sin ({\theta }_1)\\ 0& \sin ({\theta }_1)& \cos ({\theta }_1)\end{array}\right]}}\left[\begin{array}{ccc}{\sigma }_1& 0& 0\\ 0& {\sigma }_2& 0\\ 0& 0& {\sigma }_3\end{array}\right]\end{array}$$
在本例中，${\theta }_1=\pi /15，{\theta }_2=-\pi /9，{\theta }_3=-\pi /20，{\sigma }_1=3，{\sigma }_2=1，{\sigma }_3=0.5$。这些旋转矩阵并不能交换，所以旋转的顺序很重要。如果其中一个奇异值为零，则删除一个维度，椭球体将塌陷到一个低维子空间上。$R_x,R_y,R_z$是$X$在SVD 中的酉矩阵$U$。矩阵$V$是单位阵。

截断SVD

Schmidt(Gram-Schmidt 正交化方法提出者之一)将 SVD 推广到函数空间，并建立了一个近似定理，将截断 SVD作为基础矩阵$X$的最优低秩近似。Schmidt 的近似定理被Eckart 和 Young 重新发现 ，有时也被称为 Eckart -Young 定理。
定理(Eckart-Young)：最小二乘意义下$X$的最优秩$r$近似，由秩$r$SVD 截断给出:$$\underset{\tilde{\mathbf{X}},s.t.\mathrm{rank}(\tilde{\mathbf{X}})=r}{\mathrm{argmin}}\Vert \mathbf{X}-\tilde{\mathbf{X}}{\Vert }_F=\tilde{\mathbf{U}}\tilde{\mathbf{\Sigma }}{\tilde{\mathbf{V}}}^{\ast }$$其中，$\tilde{\mathbf{U}}$和$\tilde{\mathbf{V}}$可分别表示$U$和$V$中前$r$个先导列，包含中的先导$r\times r$维子块。$F$范数表示 Frobenius 范数，$\Vert \mathbf{X}{\Vert }_F=\sqrt{{\sum }_{i=1}^n{\sum }_{j=1}^m|X_{ij}{|}^2}$。
在这里，我们建立了一种表示形式，即截断SVD基(以及得到的近似矩阵)用$\tilde{\mathbf{X}}=\tilde{\mathbf{U}}\tilde{\mathbf{\Sigma }}{\tilde{\mathbf{V}}}^{\ast }$来表示。由于$\Sigma$是对角矩阵，秩$r$SVD 近似则是由$r$个不同的秩1矩阵的和给出:$$\tilde{\mathbf{X}}=\sum _{k=1}^r{\sigma }_k{\mathbf{u}}_k{\mathbf{v}}_k^{\ast }={\sigma }_1{\mathbf{u}}_1{\mathbf{v}}_1^{\ast }+{\sigma }_2{\mathbf{u}}_2{\mathbf{v}}_2^{\ast }+\cdots +{\sigma }_r{\mathbf{u}}_r{\mathbf{v}}_r^{\ast }$$这就是所谓的并向量求和。对于给定的秩$r$，在$l_2$意义下，对于$X$没有比截断 SVD 近似更好的近似。因此，高维数据可由矩阵$\tilde{\mathbf{U}}$和$\tilde{\mathbf{V}}$的列给出的几个主导模式很好地描述。

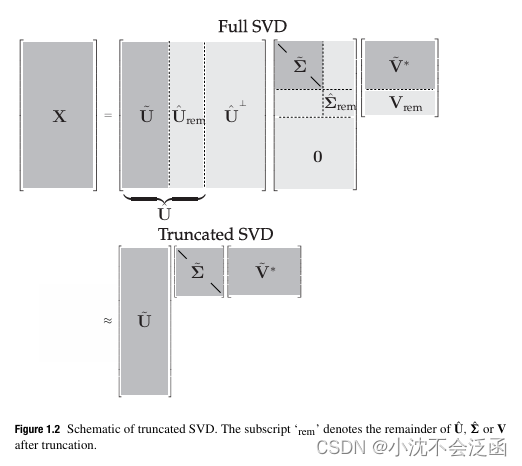
决定保留多少奇异值，即在何处开始截断，是使用SVD 时最重要和最有争议的决策之一。这其中涉及许多因素，包括对系统期望的秩的具体要求、噪声的大小以及奇异值的分布等。通常将 SVD在秩$r$处截断，以捕获原始数据中预先确定的方差或能量的数量，例如 90% 或 99% 截断。虽然很粗糙，但是这种技术是常用的。截断可被视为一种作用于奇异值上的硬阈值，大于阈值的值被保存下来，而余下的奇异值被截断。这里的最优硬阈值还有更为复杂的理论，这里便不再阐述。

PCA

这一部分也是看了B站上的视频，作者和上边推荐的一样，PCA的目标就是寻求一个坐标系在数据保留更少维度的同时信息的损失最小，目标:只保留一个轴的时候(二维降到一维)，信息保留最多，怎么样最好：找到数据分布最分散的方向(方差最大)，作为主成分(坐标轴)。
首先:去中心化(把坐标原点放在数据中心)，然后:找坐标系(找到方差最大的方向)，问题是:怎么找到方差最大的方向?我们需要保存原始的矩阵信息、新坐标系的原点、角度、新坐标点；
我们要求方差最大的方向就是求旋转的角度也就是$R$

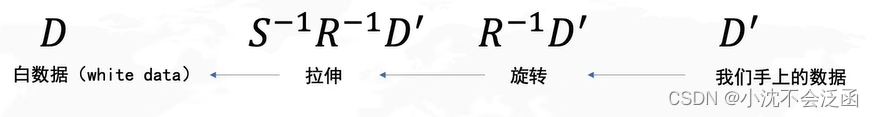
协方差矩阵的特征向量就是$R$，这话可能有些不太恰当，更直白一点就是$R$由特征向量作为列向量构成，两个变量$x,y$的协方差是$cov(x,y)=\frac{{\sum }_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{n-1}$，这里中心化以后$\bar{x}$和$\bar{y}$都为0，协方差矩阵（对称矩阵）为$$C=\left[\begin{array}{cc}cov(x,x)& cov(x,y)\\ cov(x,y)& cov(y,y)\end{array}\right]$$代入以后为：$$\begin{array}{rl}& \text{C}=\left[\begin{array}{cc}\frac{{\sum }_{i=1}^n{x_i}^2}{n-1}& \frac{{\sum }_{i=1}^n{x}_i{y}_i}{n-1}\\ \frac{{\sum }_{i=1}^n{x}_i{y}_i}{n-1}& \frac{{\sum }_{i=1}^n{y_i}^2}{n-1}\end{array}\right]=\left[\begin{array}{cccc}{x}_1& x_2& x_3& x_4\\ y_1& y_2& y_3& y_4\end{array}\right]\left[\begin{array}{cc}{x}_1& y_1\\ x_2& y_2\\ x_3& y_3\\ x_4& y_4\end{array}\right]=\frac{1}{n-1}D{D}^{\mathrm{T}}\end{array}$$其中$D$是服从正态分布的白数据，通过拉伸旋转变换得到我们手上的$D^{\prime }$，接下来的推导过程就看这个图吧，识别不动了哈哈哈：

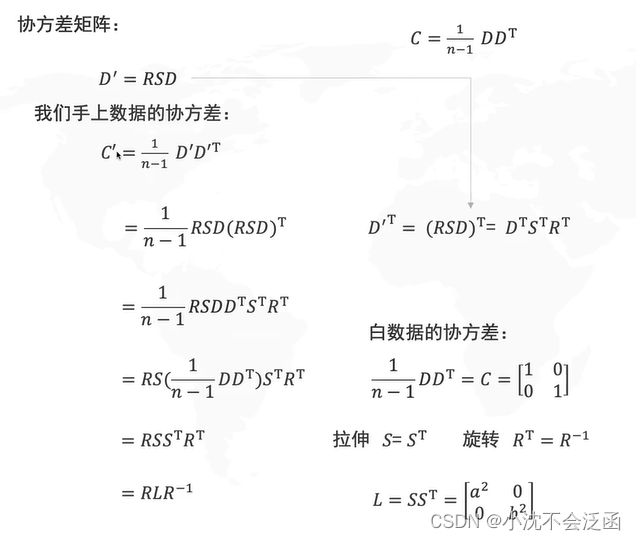
所得的$C^{\prime }=RL{R}^{-1}$说明$R$确实是协方差矩阵的特征向量，$C$:在原坐标系下的协方差，$L$:在$R$这组基下(新坐标系)的协方差；大致步骤概括如下：

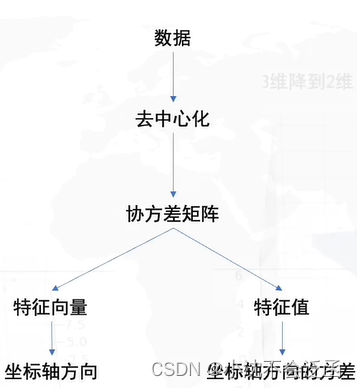
PCA与SVD还是有一定联系的，PCA中要求的$R$矩阵实际上就是SVD分解中的$V$，这句话可能所有写SVD和PCA内容的都有提到，但是很少做出了理论说明，可能没人注意到这个问题，其实我们可以看到上边的推导过程中$C^{\prime }=\frac{1}{n-1}{D}^{\prime }{D}^{\prime \mathrm{T}}=RL{R}^{-1}$说明这个$R$是$D^{\prime }{D}^{\prime \mathrm{T}}$的特征向量，那么由前边的SVD $X{X}^{\mathrm{T}}$对应的应该是$U$，而不是$V$，这个问题我在李航老师的统计学习方法中找到了答案，在第十六章326页开始：
下面也有更为详细的主成分算法：
好了这篇文章就说到这吧，文中有很多地方还是缺少理论证明，也借鉴了很多专业老师的内容来完成，对此表达崇高的谢意，有不合适的地方也希望批评指正，期待下一篇博客，耶！！！