天线的空间参量指标总结

爱跳舞的牛油果

已于 2023-07-04 22:20:07 修改

阅读量2.3k

点赞数 2

分类专栏：天线文章标签：射频工程硬件工程笔记信息与通信

于 2023-07-04 22:09:06 首次发布

本文链接：https://blog.csdn.net/weixin_54812614/article/details/131541899

版权

天线专栏收录该内容

1 篇文章

订阅专栏

本文介绍了天线的辐射场区，包括近场和远场的划分，以及方向性函数的概念，如归一化场强和功率方向性函数。讨论了天线的方向图、主瓣宽度、副瓣电平、前后比等关键参数，强调了这些参数对天线性能的影响，如增益和效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

以下内容为个人课程学习总结，仅供复习回顾参考，文中图片均取自于电子科技大学王任副教授开设的《天线原理》课程。

1.天线辐射场区

根据与天线表面的距离，天线的辐射场区可以分为近场（菲涅尔区）和远场（夫琅和费区），近场和远场的边界是菲涅耳区与夫琅和费区边界的瑞利距离，与天线尺寸与工作波长有关，其判定公式为：

$R=2D^2/\lambda$

2.方向性函数

天线的方向性函数是在离开天线一定距离处，描述天线辐射场的相对值与空间方向的函数关系。为便于比较不同天线的方向特性，通常采用归一化方向性函数。

1）归一化场强方向性函数（无量纲）

$F\left ( \theta ,\phi \right )=E_{\theta }\left ( \theta ,\phi \right )_{n}=\frac{E_{\theta }\left ( \theta ,\phi \right ) }{E_{\theta }\left ( \theta ,\phi \right )_{max}}\in \left [ 0,1 \right ]$

其中 $E_{\theta }\left ( \theta ,\phi \right )$ 为指定距离上某方向 $\left ( \theta ,\phi \right )$ 的电场强度值， $E_{\theta }\left ( \theta ,\phi \right )_{max}$ 为同一距离上的最大场强值

2）归一化功率方向性函数（无量纲）

$F_{P}\left ( \theta ,\phi \right )=P_{\theta }\left ( \theta ,\phi \right )_{n}=\frac{S\left ( \theta ,\phi \right ) }{S\left ( \theta ,\phi \right )_{max}}\in \left [ 0,1 \right ]$

其中，

$S\left ( \theta ,\phi \right )=\left [ E_{\theta }^{2}\left ( \theta ,\phi \right ) +E_{\phi }^{2}\left ( \theta ,\phi \right )\right ]/Z_{0} (W\cdot m^{-2})$

表示坡印廷矢量的幅度值， $S\left ( \theta ,\phi \right )_{max}$ 表示幅度最大值， $Z_{0}=376.7\Omega$ 表示自由空间的本征阻抗

3）二者关系

$F_{P}\left ( \theta ,\phi \right )=F^{2}\left ( \theta ,\phi \right )$

3.方向图

天线的方向性是指天线向一定方向辐射或接收电磁波的能力，天线的方向性的特性通常用方向图来表示。方向图可以按照远区电场强度大小与空间角度之间的关系绘制，也可以用功率大小绘制，功率方向图通常比场强方向图“瘦”，因为

$F_{P}\left ( \theta ,\phi \right )=F^{2}\left ( \theta ,\phi \right )$ ， $F\left ( \theta ,\phi \right )\in \left [ 0,1 \right ]$

根据归一化方向性函数可以绘制归一化方向图，归一化方向图的最大值为1。

场强归一化dB表示

$F\left ( \theta ,\phi \right )\left ( dB \right )=20lgF\left ( \theta ,\phi \right )$

功率归一化dB表示

$F_{P}\left ( \theta ,\phi \right )\left ( dB \right )=10lgF_{P}\left ( \theta ,\phi \right )$

当目标区域距离天线较远时，天线可以看做点，则可以用远场方向图（波瓣图）描述天线在不同方向的辐射情况。

对于线极化天线来说，一般情况下主要考察两个平面内的天线方向图（二维天线方向图），即E面和H面。E面表示与电场平行的平面，通常将过最大辐射方向并与电场平行的平面作为E面。 H面则是与磁场平行的平面，H面一般是指过最大辐射方向并与磁场平行的平面。二维方向图可以用极坐标表示，也可以用直角坐标表示。

4.主瓣宽度（波束宽度）

主瓣宽度又称波束宽度、3dB波束宽度、半功率波束宽度，通常指主瓣轴线两侧的两个半功率点的两条矢径之间的夹角，半功率点的衡量标准有二：①场强下降为最大值的0.707倍的点；②功率下降为最大值的一半，或者说功率比最大值低3dB（-3dB=10lg0.5）。

主瓣宽度越小，天线辐射的能量越集中，定向性越好。

主瓣宽度通常指方向图某个截面内的主瓣宽度，如果方向图不是旋转对称的，则各个截面内的主瓣宽度不等，一般考虑E面和H面。

5.副瓣电平

最大副瓣的功率密度S1与主瓣功率密度S0之比的对数值：

$SLL=10lg\left ( \frac{S_1}{S_0} \right )dB$

通常要求副瓣电平尽可能低，一般要求SLL<-20dB，低副瓣天线SLL<-30dB.

6.前后比

主瓣功率密度S0与背瓣功率密度S_b之比的对数值：

$FB=10lg\left ( \frac{S_0}{S_{b}} \right )dB$

通常要求前后比尽可能大。

7.波束立体角（波束范围）

在球面上的二维极坐标系中，微分面积 $dA$ 是沿 $\theta$ 方向(纬)的弧长 $rd \theta$ 和沿 $\phi$ 方向(经)的弧长 $r\sin \theta \cdot d\phi$ 之乘积

$dA=\left ( r d\theta \right )\left ( r \sin\theta d \phi\right )=r^2d\Omega$

其中， $d\Omega$ 表示立体角即 $dA$ 所张的立体角，表示为立体弧度（sr）或平方度。

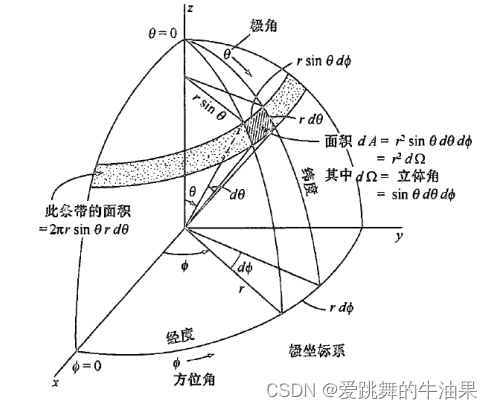
天线的波束范围，即波束立体角 $\Omega _A$ ，来自归一化功率波瓣图在球面（ $4\pi$ sr）上的积分：

$\Omega _A=\int_{\phi =0}^{\phi =2\pi}\int_{\theta =0}^{\theta =2\pi}P_n\left ( \theta ,\phi \right )\sin\theta d\theta d\phi$

和

$\Omega _A=\iint_{4\pi}P_n\left ( \theta ,\phi \right )d\Omega \left ( sr \right )$

其中， $d\Omega =\sin\theta d\theta d\phi (sr)$ .

波束立体角越小，定向性越强。

波束立体角 $\Omega _A$ 是指天线的所有辐射功率等效地按 $P_n(\theta,\phi)$ 的最大值均匀流出时的立体角。因此辐射功率 $=P_n(\theta,\phi)_{max}\Omega _A(W)$ 。而波束范围以外的辐射视为零。

8.方向性系数（定向性）

方向性系数的定义为：在相等的辐射功率下，受试天线在其最大辐射方向上某点产生的功率密度 $P_r$ 与一理想的无方向性天线在同一点产生的功率密度 $P_{ro}$ 的比值。

$D=\frac{S_{max}}{S_{0}}|_{P_r=P_{ro}}=\frac{E^2_{max}}{E^2_{0}}|_{P_r=P_{ro}}$

方向性系数的另一个计算公式：

$D=\frac{4\pi}{\Omega _A}=\frac{4\pi}{\iint_{4\pi}P_n\left ( \theta ,\phi \right )d\Omega}$

方向性系数通常指最大方向上的方向性系数。理想化的各向同性天线( $\Omega _A=4\pi sr$ )具有最低可能的定向性D=1,而所有实际天线的定向性都大于1 (D>1)。方向性系数越大，定向性越好。

电偶极子的方向性系数D=1.5，D(dB)=10lg1.5=1.76dB.

9.效率

天线的效率表征天线将输入高频能量转换为无线电波能量的有效程度，其定义为天线的辐射功率 $P_r$ 与输入功率 $P_{in}$ 的比值：

$\eta =\frac{P_r}{P_{in}}=\frac{P_r}{P_{r}+P_L}$

其中， $P_L$ 为天线的总损耗功率，包括天线导体中的损耗和介质材料中的损耗。

10.增益Gain

增益表征将输入给天线的功率按特定方向辐射的能力，其定义为：在相等的输入功率下，受试天线在其最大辐射方向上某点产生的功率密度 $P_{in}$ 与一理想的无方向性天线在同一点产生的功率密度 $P_{ino}$ 的比值。

$G=\frac{S_{max}}{S_{0}}|_{P_{in}=P_{ino}}=\frac{E^2_{max}}{E^2_{0}}|_{P_{in}=P_{ino}}$

增益的另一个定义为方向性系数与效率的乘积：

$G=\eta \cdot D$

一般来说，天线的主板波束宽度越窄，天线增益越高。

11.口径Aperture

从接收天线的观点引入口径的概念。假设接收天线是置于均匀平面电磁波中的矩形电磁喇叭，记平面波的功率密度即坡印廷矢量的幅度为S (W/m²)，喇叭的物理口径即面积为Ap(m²)。如果喇叭以其整个物理口径从来波中摄取所有的功率，则喇叭吸收的总功率为

$P=\frac{E^2}{Z}A_p=S\cdot A_p\left ( W \right )$

于是，可认为电磁喇叭从来波中摄取的总功率正比于某--种口径的面积。

但是喇叭对来波的响应并非是均匀的口径场分布，因为侧壁上的电场E必须等于零。

12.口径效率

口径效率定义为有效口径Ae与物理口径Ap之比：

$\xi_{ap} =\frac{A_e}{A_p}$

对于喇叭和抛物面反射镜天线而言，口径效率普遍在50% ~ 80% (即 $0.5\leq \xi _{ap}\leq 0.8$ )的范围内，而对于在物理口径边缘也能维持均匀场的偶极子或贴片大型阵列来说，口径效率则可以接100%，然而，要降低旁瓣就必须采用向边缘锥削的口径场分布，这必然导致口径效率的下降。