MPC学习推导

已于 2025-01-17 18:23:16 修改
阅读量444 收藏 11
点赞数 5
文章标签： 学习 c++ matlab
于 2023-12-03 22:12:26 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_55365829/article/details/134771156
版权

一、理论推导

系统离散化后的状态空间方程表达式如下：

x(k+1)=Ax(k)+Bu(k)

基于离散化状态空间表达式，即可预测个步长之后的状态变量转移情况，公式如下：

如果预测区间为，则可以将每步状态转移写出如下矩阵的形式：

式中， ，
.

由于目标函数被写为：

式中，，.

将公式（14）转化为关于的二次规划问题，得到

式中，，.

在不考虑边界约束的条件下，求目标函数对的偏导，即可得出得到最优控制率：

针对一个实际问题，控制系统不可能没有约束条件，因此对二次规划问题引入边界条件限制。一般来说，常见的约束为盒状约束。约束条件包括控制约束与输出约束，状态变量约束由于可以通过输出矩阵逆变换得到，因此被等效为输出约束。

约束条件如下：

将公式（17）写为增广矩阵不等式的形式可得：

其中, ,

为了得到关的约束条件，还需要预测个步长之后的约束条件，因此写出其增广矩阵的形式：

式中，, , ,

整理上式可得二次规划问题的约束条件：

式中

在MATLAB-Simulink中使用quadprog求解带约束条件的二次规划问题。

其中H为H，F为F，state为x(k),Akappa为，vat为，Wkappa

opts = optimoptions('quadprog','Algorithm','active-set');
uk=quadprog(H,F*state,Akappa,vat+Wkappa*state,[],[],[],[],x0,opts);

二、实际问题

采用线性二自由度模型，进行轨迹跟踪MPC控制。横纵向速度解耦，纵向速度被设为定值。

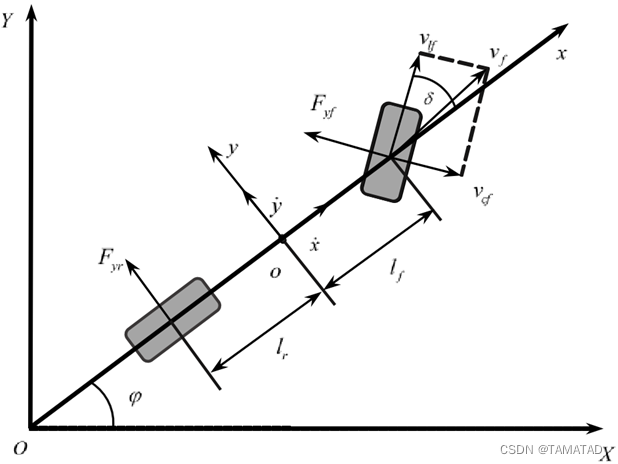
车辆线性二自由度状态空间方程：

式中，状态变量，控制变量。

由上式可知，系统的状态变量包括横向速度、横摆角速度、横摆角误差和横向位移误差。系统输入为前轮转角和纵向速度干扰。其中前轮转角为系统控制量，是轨迹跟踪实现的核心，而纵向干扰认为是干扰项。

三、代码

1、matlab

在MATLAB中生成这些相关矩阵（定常系统无所谓实时更新）

Np = 10;     %prediction step
Nc = 1;      %control step
Ts = 0.0005;

vx =80/3.6;
L1=2.0;L2=2.2;
m=4000;
Izz = 12000;

Cf = 6e7*pi/180;                                                       %前轮侧偏刚度
Cr = 5e7*pi/180;                                                       %后轮侧偏刚度
a11 = (Cf+Cr)/m/vx;                                       
a12 = (Cf*L1-Cr*L2)/m/vx-vx;                  
a21 = (Cf*L1-Cr*L2)/Izz/vx;
a22 = (Cf*L1^2 + Cr*L2^2)/Izz/vx;
b11 = Cf/m;
b21 = Cf*L1/Izz;


A = [a11 a12 0 0;a21 a22 0 0;0 1 0 0;1 0 vx 0];
B = [b11 0;b21 0;0 -vx;0 0];
C = eye(4);
n=size(A,1);
p=size(B,2);
P=[10 0 0 0;
    0 10 0 0;
    0 0 10 0;
    0 0 0 1000];
Q=[1 0 0 0;
    0 1 0 0;
    0 0 100 0;
    0 0 0 1000];
R=[100,0;
    0,0];

[A,B]=discrete_model(A,B,Ts);%调用外部函数


%%%%测试用，看静态状态收敛情况如何
X_k=zeros(n,Np);
X_k(:,1)=[0.01,0.01,-0.18,-3.9];
U_k=zeros(p,Np);

%%%%%无约束增广矩阵
phi=cell(Np,1);
for i=1:Np
    phi{i,1}=A^i;
end
phi=cell2mat(phi);

gama=cell(Np,Np);
for i=1:Np
    for k=1:Np
        if i>=k
            gama{i,k}=A^(i-k)*B;
        else
            gama{i,k}=zeros(size(A*B,1),size(A*B,2));
        end
    end
end
gama=cell2mat(gama);

omiga=cell(Np,Np);
for i=1:Np
    for k=1:Np
        if i==k
            omiga{i,k}=Q;
        else
            omiga{i,k}=zeros(size(Q,1),size(Q,2));
        end
    end
end
omiga{Np,Np}=P;
omiga=cell2mat(omiga);


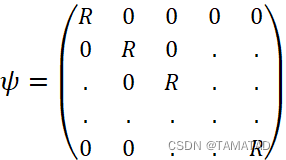
psi=cell(Np,Np);
for i=1:Np
    for k=1:Np
        if i==k
            psi{i,k}=R;
        else
            psi{i,k}=zeros(size(R,1),size(R,2));
        end
    end
end
psi=cell2mat(psi);


%%%%%%无约束的最优空置率矩阵
H=2*(psi+gama'*omiga*gama);
F=2*gama'*omiga*phi;
G=Q+phi'*omiga*phi;

%%%%%%%开始考虑约束
M=cell(4,1);
M{1,1}=zeros(size(B,2),size(C,2));
M{2,1}=zeros(size(B,2),size(C,2));
M{3,1}=-C;
M{4,1}=C;
M=cell2mat(M);

Mn=cell(2,1);
Mn{1,1}=-C;
Mn{2,1}=C;
Mn=cell2mat(Mn);

E=cell(4,1);
E{1,1}=-eye(size(B,2));
E{2,1}=eye(size(B,2));
E{3,1}=zeros(size(B,1),size(B,2));
E{4,1}=zeros(size(B,1),size(B,2));
E=cell2mat(E);

ul=[-30/180*pi;-10];
uh=[30/180*pi;10];
yl=-0.1*[1;0.3;0.1;0.3];
yh=0.1*[1;0.3;0.1;0.3];
% yl=-0.1*[1;0.3;0.1;0.3];
% yh=0.1*[1;0.3;0.1;0.3];

bi=cell(4,1);
bi{1,1}=-ul;
bi{2,1}=uh;
bi{3,1}=-yl;
bi{4,1}=yh;
bi=cell2mat(bi);

bN=cell(2,1);
bN{1,1}=-yl;
bN{2,1}=yh;
bN=cell2mat(bN);

Mat=cell(Np+1,Np);
for i=1:Np
    for k=1:Np
        if i==k+1
            Mat{i,k}=M;
        else
            Mat{i,k}=zeros(size(M,1),size(M,2));
        end
    end
end
for k=1:Np
    if k==Np
        Mat{Np+1,k}=Mn;
    else
        Mat{Np+1,k}=zeros(size(Mn,1),size(Mn,2));
    end
end
Mat=cell2mat(Mat);

Det=cell(Np+1,1);
for i=1:Np+1
   if i==1
       Det{i,1}=M;
   elseif i==Np+1
        Det{i,1}=zeros(size(Mn,1),size(M,2));
   else
       Det{i,1}=zeros(size(M,1),size(M,2));
   end
end
Det=cell2mat(Det);


kase=cell(Np+1,Np);
for i=1:Np
    for k=1:Np
        if i==k
            kase{i,k}=E;
        else
            kase{i,k}=zeros(size(E,1),size(E,2));
        end
    end
end
for k=1:Np
    kase{Np+1,k}=zeros(size(Mn,1),size(E,2));
end
kase=cell2mat(kase);

vat=cell(Np+1,1);
for i=1:Np+1
   if i==Np+1
       vat{i,1}=bN;
   else
       vat{i,1}=bi;
   end
end
vat=cell2mat(vat);


%%%%%%%%%带约束的矩阵条件，quadprog中的A b
Akappa=Mat*gama+kase;
Wkappa=-Det-Mat*phi;


x0=zeros(size(H,1),1);
opts = optimoptions('quadprog','Algorithm','active-set');
uk=quadprog(H,F*X_k(:,1),Akappa,vat+Wkappa*X_k(:,1),[],[],[],[],x0,opts);
u=uk(2,:)%测试
2、Simulink

在simlink中调用这些这些矩阵，即可求出控制函数u

function u = fcn(state,H,F,Akappa,vat,Wkappa)
u=0;
x=size(H,1);
x0=zeros(x,1);
opts = optimoptions('quadprog','Algorithm','active-set');
uk=quadprog(H,F*state,Akappa,vat+Wkappa*state,[],[],[],[],x0,opts);
u=uk(1,:);

整体架构

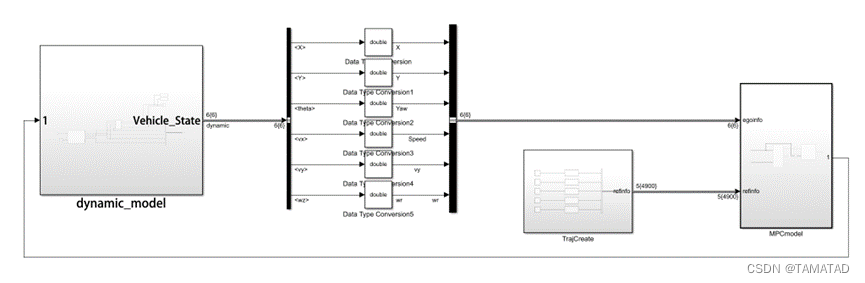
MPC控制模块

横向位移偏差和横摆角偏差生成

function [path,Vref, Poseref] = planner_power5(Xa,Ya,YAW, Xr, Yr, PHIr, K, Vr)
X = Xa;
Y = Ya;
PHI = YAW;
Poseref = zeros(1,3);
 %%%选择参考点
%  X = 50;
%  Y = 2.5;
t = 0:0.05:48.95;
px = spline(t,Xr);
py = spline(t,Yr);
pv = spline(t,Vr);
pk = spline(t,K);
pphi = spline(t,PHIr);

[INDEX,~] = search([Xr;Yr]',[X Y]);
if(INDEX == 980)
    upper = INDEX;
    lower = INDEX-2;

else
    if(INDEX >1)
        upper = INDEX+1;
        lower = INDEX-1;
    else
        upper = INDEX+2;
        lower = INDEX;
    end 
end
tt = linspace(t(lower),t(upper),51);
xx = ppval(px,tt);
yy = ppval(py,tt);
phi = ppval(pphi,tt);
vr= ppval(pv,tt);
[index,dist] = search([xx;yy]',[X Y]);

% %plot(X,Y,'*');
% %plot(Xr(index),Yr(index),'-o');
%dist = sqrt((X-Xr(index1))^2+(Y-Yr(index1))^2);
if(((Y-yy(index))*cos(phi(index)) - (X-xx(index))*sin(phi(index)))>0)
    ed = dist;%在目标曲线左侧为正
else
    ed = -dist;
end

ePHI = PHI - phi(index);
%path = [ePHI,ed,K(index:index+19)];
kr = ppval(pk,linspace(tt(index),tt(index)+0.025*19,20));
path=[0,0];
path = [ePHI,ed];
Vref = vr(index);
Poseref = [xx(index),yy(index),phi(index)];
% path = [Xr(index+1:index+20),Yr(index+1:index+20),atan(PHIr(index+1:index+20))];


function [index,dist] = search(ref,pose)
 index = 1;
 dist = sqrt((pose(1)-ref(1,1))^2 + (pose(2)-ref(1,2))^2);
    for i = 1:size(ref,1)
        dist_temp = sqrt((pose(1)-ref(i,1))^2 + (pose(2)-ref(i,2))^2);
        if(dist_temp < dist)
            dist = dist_temp;
            index = i;
        end
    end
3、CPP

在ros环境下写了一个cpp版本的MPC类，按照MATLAB方法进行实现。

#include <ros/ros.h>
#include <sensor_msgs/JointState.h>
#include <tf/transform_broadcaster.h>
#include <nav_msgs/Odometry.h>
#include "nav_msgs/Path.h"
#include <iostream>
#include <vector>
#include <deque>
#include <eigen3/Eigen/Dense>
#include <eigen3/Eigen/Sparse>
#include <OsqpEigen/OsqpEigen.h>
#include <unsupported/Eigen/MatrixFunctions>
#include <Eigen/SVD>

struct Point
{   //nav_msgs/Path doesn't have kappa message so using it to desicribe kappa
    double x,y,yaw,kappa;
    Point() : x(0),y(0),yaw(0),kappa(0) {};
    Point(double x,double y,double yaw,double kappa) : x(x),y(y),yaw(yaw),kappa(kappa) {};
};

struct Vehicle
{   
    //Default vehicle is a truck for test , for you vehicle please using param construction
    double Cf , Cr , mass , lf , lr , Intieral;
    Vehicle(){
        Cf = -6e7*M_PI/180 , Cr = -5e7*M_PI/180 , mass = 4000 , lf = 2.0 , lr = 2.2 , Intieral = 12000;
    };
    //Cf, Cr must be minus!!!
    Vehicle(double Cf ,double Cr ,double mass ,double lf ,double lr ,double Intieral) : Cf(Cf),Cr(Cr),mass(mass),lf(lf),lr(lr),Intieral(Intieral){};
};

class MPCcontrol
{
private:
public:
    MPCcontrol(Vehicle veh, std::vector<double> state, int PredictStep , double current_velocity , bool Construct);
    ~MPCcontrol();
    bool getControl(double& target_angle);
    void ConstructMatrix();
    void SetBoundary(double ul,double uh,std::vector<double> xl,std::vector<double> xh);
    void SetWeight(std::vector<double> Qw,double Rw,std::vector<double> Pw);
    int PredictStep;
    double delta_t;
    Vehicle vehicle;
    Eigen::MatrixXd A_Matrix;
    Eigen::MatrixXd B_Matrix;
    Eigen::MatrixXd Q_Matrix;
    Eigen::MatrixXd R_Matrix;
    Eigen::MatrixXd P_Matrix;
    Eigen::MatrixXd X_state;
    Eigen::MatrixXd PHI_Matrix;
    Eigen::MatrixXd GAMA_Matrix;
    Eigen::MatrixXd OMIGA_Matrix;
    Eigen::MatrixXd PSI_Matrix;
    Eigen::MatrixXd H_Matrix;
    Eigen::MatrixXd F_Matrix;
    Eigen::MatrixXd W_Matrix;
    Eigen::MatrixXd Abias_Matrix;
    Eigen::MatrixXd C_Matrix;
    Eigen::MatrixXd M_Matrix;
    Eigen::MatrixXd MN_Matrix;
    Eigen::MatrixXd E_Matrix;
    Eigen::MatrixXd b_Matrix;
    Eigen::MatrixXd bN_Matrix;
    Eigen::MatrixXd Dbias_Matrix;
    Eigen::MatrixXd Mbias_Matrix;
    Eigen::MatrixXd Vbias_Matrix;
    Eigen::MatrixXd KESI_Matrix;

    Eigen::MatrixXd ul;
    Eigen::MatrixXd uh;
    Eigen::MatrixXd yl;
    Eigen::MatrixXd yh;

};

MPCcontrol::MPCcontrol(Vehicle veh, std::vector<double> state , int PredictStep , double current_velocity , bool Construct = false)
{   
    //direct_get
    double speed;
    if(fabs(current_velocity - 1e-1) < 1e-3){
        speed = 1;
    }
    else{
        speed = current_velocity;
    }
    this->PredictStep = PredictStep;
    this->vehicle = veh;
    this->X_state = Eigen::MatrixXd(1,4).setZero();
    this->X_state(0) = state[0];
    this->X_state(1) = state[1];
    this->X_state(2) = state[2];
    this->X_state(3) = state[3];
    this->A_Matrix = Eigen::MatrixXd(4,4).setZero();
    this->A_Matrix(0,1) = 1;
    this->A_Matrix(1,1) = (this->vehicle.Cf + this->vehicle.Cr) / this->vehicle.mass /speed;
    this->A_Matrix(1,2) = -(this->vehicle.Cf + this->vehicle.Cr) / this->vehicle.mass;
    this->A_Matrix(1,3) = (this->vehicle.Cf *this->vehicle.lf - this->vehicle.Cr*this->vehicle.lr) / this->vehicle.mass /speed;
    this->A_Matrix(2,3) = 1;
    this->A_Matrix(3,1) = (this->vehicle.Cf *this->vehicle.lf - this->vehicle.Cr*this->vehicle.lr) / this->vehicle.Intieral /speed;
    this->A_Matrix(3,2) = -(this->vehicle.Cf *this->vehicle.lf - this->vehicle.Cr*this->vehicle.lr) / this->vehicle.Intieral;
    this->A_Matrix(3,3) = (this->vehicle.Cf *this->vehicle.lf*this->vehicle.lf + this->vehicle.Cr*this->vehicle.lr*this->vehicle.lr) / this->vehicle.Intieral /speed;
    this->B_Matrix = Eigen::MatrixXd(4,1).setZero();
    this->B_Matrix(1,0) = -this->vehicle.Cf /this->vehicle.mass;
    this->B_Matrix(3,0) = -this->vehicle.Cf*this->vehicle.lf / this->vehicle.Intieral;
    // forward Euler
    this->delta_t = 0.001;
    // this->A_Matrix = this->A_Matrix * this->delta_t + Eigen::MatrixXd(4,4).setIdentity();
    // this->B_Matrix = this->B_Matrix * this->delta_t;
    Eigen::MatrixXd Ad = (this->delta_t * this->A_Matrix).exp();
    Eigen::MatrixXd Bd = Eigen::MatrixXd::Zero(this->A_Matrix.rows(), this->B_Matrix.cols());
    double h = this->delta_t / 100; // 假设将区间[0, T]分成100个小区间
    for (int i = 0; i <= 100; ++i) {
        double s = i * h;
        Eigen::MatrixXd exp_As = (this->A_Matrix * s).exp() * this->B_Matrix *h;
        Bd += exp_As;
    }
    this->A_Matrix = Ad;
    this->B_Matrix = Bd;
    // std::cout << "this->A_Matrix" << "\n";
    // std::cout << this->A_Matrix << "\n";
    // std::cout << "this->B_Matrix" << "\n";
    // std::cout << this->B_Matrix << "\n";

    //Pre weights
    this->Q_Matrix = Eigen::MatrixXd(4,4).setIdentity();
    this->Q_Matrix(0,0) = 100;
    this->Q_Matrix(2,2) = 10;
    this->R_Matrix = Eigen::MatrixXd(1,1).setIdentity();
    this->P_Matrix = Eigen::MatrixXd(4,4).setIdentity();
    this->P_Matrix(0,0) = 100;
    this->P_Matrix(1,1) = 10;
    this->P_Matrix(2,2) = 10;
    this->P_Matrix(3,3) = 10;

    //Pre Boundary
    this->ul = Eigen::MatrixXd(1,1);
    ul(0,0) = (double)-40/180*M_PI;
    this->uh = Eigen::MatrixXd(1,1);
    uh(0,0) = (double)40/180*M_PI;
    this->yl = Eigen::MatrixXd(4,1).setZero();
    yl(0,0) = (double)-10 , yl(1,0) = (double)-5;
    yl(2,0) = (double)-10 , yl(3,0) = (double)-5;
    this->yh = Eigen::MatrixXd(4,1).setZero();
    yh(0,0) =( double)10 , yh(1,0) = (double)5;
    yh(2,0) =( double)10 , yh(3,0) = (double)5;

    if(Construct){
        std::cout << "Constructed Matrix in Pre-Construction Function" << "\n";
        ConstructMatrix();
    }

};
void MPCcontrol::SetBoundary(double ul,double uh,std::vector<double> xl,std::vector<double> xh){
    //Change boundary if you want
    this->ul = Eigen::MatrixXd(1,1);
    this->ul(0,0) = ul;
    this->uh = Eigen::MatrixXd(1,1);
    this->uh(0,0) = uh;
    this->yl = Eigen::MatrixXd(4,1).setZero();
    yl(0,0) = xl[0] , yl(1,0) = xl[1];
    yl(2,0) = xl[2] , yl(3,0) = xl[3];
    this->yh = Eigen::MatrixXd(4,1).setZero();
    yh(0,0) = xh[0] , yh(1,0) = xh[1];
    yh(2,0) = xh[2] , yh(3,0) = xh[3];
};
void MPCcontrol::SetWeight(std::vector<double> Qw,double Rw,std::vector<double> Pw){
    //Change weights if you want
    this->Q_Matrix = Eigen::MatrixXd(4,4).setIdentity();
    this->Q_Matrix(0,0) = Qw[0];
    this->Q_Matrix(1,1) = Qw[1];
    this->Q_Matrix(2,2) = Qw[2];
    this->Q_Matrix(3,3) = Qw[3];
    this->R_Matrix = Eigen::MatrixXd(1,1).setIdentity();
    this->R_Matrix(0,0) = Rw;
    this->P_Matrix = Eigen::MatrixXd(4,4).setIdentity();
    this->P_Matrix(0,0) = Pw[0];
    this->P_Matrix(1,1) = Pw[1];
    this->P_Matrix(2,2) = Pw[2];
    this->P_Matrix(3,3) = Pw[3];
}
void MPCcontrol::ConstructMatrix(){
    //have to solve
    this->PHI_Matrix = Eigen::MatrixXd(4*this->PredictStep,4).setZero();
    Eigen::MatrixXd psi(4,4);
    psi.setIdentity();
    for(int i=0;i<this->PredictStep;i++){
        psi *= this->A_Matrix;
        this->PHI_Matrix.block(i*4,0,4,4) = psi;
    }
    // std::cout << "this->PHI_Matrix" << "\n";
    // std::cout << this->PHI_Matrix << "\n";
    this->GAMA_Matrix = Eigen::MatrixXd(4*this->PredictStep,1*this->PredictStep).setZero();
    Eigen::MatrixXd gama = this->B_Matrix;
    for(int i=0;i<this->PredictStep;i++){
        for(int j=0;j<this->PredictStep-i;j++){
            this->GAMA_Matrix.block(4*(i+j),1*j,4,1) = gama;
        }
        gama  = this->A_Matrix * gama;
    }
    // std::cout << "this->GAMA_Matrix" << "\n";
    // std::cout << this->GAMA_Matrix << "\n";

    this->OMIGA_Matrix = Eigen::MatrixXd(4*this->PredictStep,4*this->PredictStep).setZero();
    for(int i=0;i<this->PredictStep-1;i++){
        this->OMIGA_Matrix.block(4*i,4*i,4,4) = this->Q_Matrix;
    }
    this->OMIGA_Matrix.block(4*(this->PredictStep-1),4*(this->PredictStep-1),4,4) = this->P_Matrix;
    // std::cout << "this->OMIGA_Matrix" << "\n";
    // std::cout << this->OMIGA_Matrix << "\n";
    this->PSI_Matrix = Eigen::MatrixXd(1*this->PredictStep,1*this->PredictStep).setZero();
    for(int i=0;i<this->PredictStep;i++){
        this->PSI_Matrix.block(1*i,1*i,1,1) = this->R_Matrix;
    }
    // std::cout << "this->PSI_Matrix" << "\n";
    // std::cout << this->PSI_Matrix << "\n";
    this->H_Matrix = 2*(this->PSI_Matrix + this->GAMA_Matrix.transpose()*this->OMIGA_Matrix*this->GAMA_Matrix);
    this->F_Matrix = 2*(this->GAMA_Matrix.transpose()*this->OMIGA_Matrix*this->PHI_Matrix);
    // std::cout << "this->H_Matrix" << "\n";
    // std::cout << this->H_Matrix << "\n";
    // std::cout << "this->F_Matrix" << "\n";
    // std::cout << this->F_Matrix << "\n";

    // Box constraints have to solve
    this->C_Matrix = Eigen::MatrixXd(4,4).setIdentity();
    // this->C_Matrix(0,0) = 1 , this->C_Matrix(1,1) = 1;
    this->M_Matrix = Eigen::MatrixXd(1*2+4*2,4).setZero();
    this->M_Matrix.block(2,0,4,4) = -this->C_Matrix;
    this->M_Matrix.block(6,0,4,4) = this->C_Matrix;
    this->MN_Matrix = Eigen::MatrixXd(4*2,4).setZero();
    this->MN_Matrix.block(0,0,4,4) = -this->C_Matrix;
    this->MN_Matrix.block(4,0,4,4) = this->C_Matrix;

    this->E_Matrix = Eigen::MatrixXd(1*2+4*2,1).setZero();
    this->E_Matrix.block(0,0,1,1) = -Eigen::MatrixXd(1,1).setIdentity();
    this->E_Matrix.block(1,0,1,1) =  Eigen::MatrixXd(1,1).setIdentity();

    
    this->b_Matrix = Eigen::MatrixXd(1*2+4*2,1).setZero();
    this->b_Matrix.block(0,0,2,1) = -this->ul;
    this->b_Matrix.block(1,0,2,1) =  this->uh;
    this->b_Matrix.block(2,0,4,1) = -this->yl;
    this->b_Matrix.block(6,0,4,1) =  this->yh;
    this->bN_Matrix = Eigen::MatrixXd(4*2,1).setZero();
    this->bN_Matrix.block(0,0,4,1) = -this->yl;
    this->bN_Matrix.block(4,0,4,1) =  this->yh;
    // std::cout << "this->b_Matrix" << "\n";
    // std::cout << b_Matrix << "\n";
    // std::cout << "this->bN_Matrix" << "\n";
    // std::cout << bN_Matrix << "\n";

    this->Dbias_Matrix = Eigen::MatrixXd(this->M_Matrix.rows()*this->PredictStep+this->MN_Matrix.rows(),this->M_Matrix.cols()).setZero();
    this->Dbias_Matrix.block(0,0,this->M_Matrix.rows(),this->M_Matrix.cols()) = this->M_Matrix;
    // std::cout << "this->Dbias_Matrix" << "\n";
    // std::cout << this->Dbias_Matrix << "\n";
    
    this->Mbias_Matrix = Eigen::MatrixXd(this->M_Matrix.rows()*this->PredictStep+this->MN_Matrix.rows(),this->M_Matrix.cols()*this->PredictStep).setZero();
    for(int i=1;i<this->PredictStep;i++){
        this->Mbias_Matrix.block(this->M_Matrix.rows() * i,this->M_Matrix.cols() * (i-1),this->M_Matrix.rows(),this->M_Matrix.cols()) = this->M_Matrix;
    }
    this->Mbias_Matrix.block(this->M_Matrix.rows() * this->PredictStep,this->M_Matrix.cols() * (this->PredictStep-1),this->MN_Matrix.rows(),this->MN_Matrix.cols()) = this->MN_Matrix;
    // std::cout << this->Mbias_Matrix << "\n";
    // std::cout << this->Mbias_Matrix.rows() << "\n" << this->Mbias_Matrix.cols();


    this->KESI_Matrix = Eigen::MatrixXd(this->E_Matrix.rows()*this->PredictStep+this->MN_Matrix.rows(),this->E_Matrix.cols()*this->PredictStep).setZero();
    for(int i=0;i<this->PredictStep;i++){
        this->KESI_Matrix.block(this->E_Matrix.rows() * i,this->E_Matrix.cols() * i,this->E_Matrix.rows(),this->E_Matrix.cols()) = this->E_Matrix;
    }
    // std::cout << this->KESI_Matrix << "\n";

    this->Vbias_Matrix = Eigen::MatrixXd(this->b_Matrix.rows()*this->PredictStep+this->bN_Matrix.rows(),this->b_Matrix.cols()).setZero();
    for(int i=0;i<this->PredictStep;i++){
        this->Vbias_Matrix.block(this->b_Matrix.rows() * i,0,this->b_Matrix.rows(),this->b_Matrix.cols()) = this->b_Matrix;
    }
    this->Vbias_Matrix.block(this->b_Matrix.rows() * this->PredictStep,0,this->bN_Matrix.rows(),this->bN_Matrix.cols()) = this->bN_Matrix;
    // std::cout << this->Vbias_Matrix << "\n";
    
    this->Abias_Matrix = this->Mbias_Matrix * this->GAMA_Matrix + this->KESI_Matrix;
    this->W_Matrix = -this->Dbias_Matrix - this->Mbias_Matrix * this->PHI_Matrix;
    // std::cout << "this->Abias_Matrix" << "\n";
    // std::cout << this->Abias_Matrix << "\n";
    // std::cout << "this->W_Matrix" << "\n";
    // std::cout << this->W_Matrix << "\n";
}

bool MPCcontrol::getControl(double& target_angle){

    Eigen::SparseMatrix<double> hessian = this->H_Matrix.sparseView(1e-10);
    // Eigen::JacobiSVD<Eigen::MatrixXd> svd(this->H_Matrix);
	// std::cout << "this->H_Matrix rank= " <<svd.rank()<< "\n";
	// std::cout << "hessian rows= " <<hessian.rows()<< "hessian cols= " <<hessian.cols() << "\n";
    Eigen::VectorXd gradient = (this->F_Matrix * this->X_state);
    Eigen::SparseMatrix<double> linearMatrix = this->Abias_Matrix.sparseView(1e-10);
    Eigen::VectorXd upperBound = (this->Vbias_Matrix+this->W_Matrix*this->X_state);
    Eigen::VectorXd lowerBound;
    lowerBound.resize(upperBound.rows());
    for(int i=0;i<upperBound.rows();i++){
        lowerBound[i] = -100000;
    }
	// std::cout << "upperBound= \n" <<upperBound<< "\nlowerBound= \n" <<lowerBound << "\n";

    int NumberOfVariables = this->Abias_Matrix.cols();   //A矩阵的列数
    int NumberOfConstraints = this->Abias_Matrix.rows(); //A矩阵的行数
	// std::cout << "NumberOfVariables= " <<NumberOfVariables<< "  NumberOfConstraints= " <<NumberOfConstraints << "\n";

    OsqpEigen::Solver solver;

    // settings
    solver.settings()->setVerbosity(false);
    solver.settings()->setWarmStart(true);

    // set the initial data of the QP solver
    //矩阵A为m*n矩阵
    solver.data()->setNumberOfVariables(NumberOfVariables);     //设置A矩阵的列数，即n
    solver.data()->setNumberOfConstraints(NumberOfConstraints); //设置A矩阵的行数，即m
    if (!solver.data()->setHessianMatrix(hessian))
        return false; //设置P矩阵
    if (!solver.data()->setGradient(gradient))
        return false; //设置q or f矩阵。当没有时设置为全0向量
    if (!solver.data()->setLinearConstraintsMatrix(linearMatrix))
        return false; //设置线性约束的A矩阵
    if (!solver.data()->setLowerBound(lowerBound))
        return false; //设置下边界
    if (!solver.data()->setUpperBound(upperBound))
        return false; //设置上边界

    // instantiate the solver
    if (!solver.initSolver())
        return false;

    Eigen::VectorXd QPSolution;

    // solve the QP problem
    if (!solver.solve())
        return false;

    // get the controller input
    clock_t time_start = clock();
    clock_t time_end = clock();
    time_start = clock();
    QPSolution = solver.getSolution();
    time_end = clock();
    std::cout << "time use:" << 1000 * (time_end - time_start) / (double)CLOCKS_PER_SEC << "ms" << std::endl;

    // std::cout << "QPSolution:" << std::endl
    //             << QPSolution << std::endl;
    target_angle = QPSolution[0];
    return true;

}


MPCcontrol::~MPCcontrol()
{
}

TAMATAD
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值