Graph Primitves - Dijkstra’s Algorithm

Part 1 The Basics

1. Single-Source Shortest Paths（单源最短路径）

 Length of path = sum of edge lengths【路径长度 = 边长度之和】

Input: directed graph G=(V, E). (m=|E|, n=|V| )

• each edge has non negative length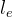

• source vertex s

【输入：有向图G=(V、E）。（m=|E|，n=|V|）。每条边的长度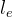是非负的；源顶点s。】

Output: for each , compute

L(v) := length of a shortest s-v path in G

【输出：对于每一个，计算，L(v) = G中最短的 s-v 路径的长度】

Assumption:

One of the following is the list of shortest-path distances for the nodes s，v，w，t, respectvely. Which is it?【其中一个是节点s.v.w.t的最短路径距离列表。是哪一个？】

2.Why Another Shortest-Path Algorithm?【为什么是另一个最短路径算法？】

Question: doesn’t BFS already compute shortest paths in linear time?

【问：难道BFS不是已经在线性时间内计算出最短路径了吗？】

Answer: yes, IF 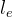= 1 for every edge e.  

【回答：是的，如果le = 1对于每条边e。】

Question: why not just replace each edge e by directed path of 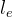unit length edges:

【问：为什么不把每条边e替换为有向路径的单位长度边：】

Answer: blows up graph too much

【回答：把图表搞得太多了】

Solution: Dijkstra’s shortest path algorithm.

【解决方案：Dijkstra的最短路径算法。】

3.Dijkstra’s Algorithm

 

 4.Non-Example

 

Question: why not reduce computing shortest paths with negative edge lengths to the same problem with non negative lengths? (by adding large constant to edge lengths)

【问：为什么不将计算具有负边长度的最短路径减少到具有非负边长度的相同问题呢？（通过向边长度添加大常量）】

Problem: doesn’t preserve shortest paths !

【问题：不能保留最短的路径！】

Also: Dijkstra’s algorithm incorrect on this graph !

【另外：Dijkstra的算法在这个图上是不正确的！】

(computes shortest s-t distance to be -2 rather than -4) 【（计算最短的s-t距离为-2，而不是-4)】

Part 2 Why It Works

1.Correctness Claim【正确性声明】

Theorem【定理】  [Dijkstra] For every directed graph with nonnegative edge lengths, Dijkstra’s algorithm correctly computes all shortest-path distances.

【对于每一个具有非负边长度的有向图，Dijkstra的算法正确地计算了所有的短路径距离。】

 Proof【证明】: by induction on the number of iterations. 【通过对迭代次数的归纳法。】

Base Case【基本情况】:

 2.Proof【证明】

Inductive Step【归纳步骤】:

Inductive Hypothesis: all previous iterations correct (i.e., A[v] = L(v) and B[v] is a true shortest s-v path in G, for all v already in X).

【归纳假设：所有之前的迭代都是正确的（即，A[v] = L (v)和B[v]是G中一个真正的最短的s-v路径，对于X中已经存在的所有v）。】

 3.Proof（con'd）

 

 Part 3 Fast Implementation【快速实现】

Which of the following running *mes seems to best describe a “naïve” implementa*on of Dijkstra’s algorithm?【下面哪一个运行方法似乎最能描述Dijkstra算法的“幼稚”实现？】