1.真值表法
根据重言式的定义,即一个公式φ是重言式当且仅当对所有赋值v,v(φ)=1,于是我们对此命题逻辑的所有原子命题进行赋值来判断是否是重言式。

如:(p∨q)→(p∧q)
可见原式的结果不为全为1或不全为0,因此原式为重言式。
2.归谬赋值法
在命题逻辑中,析取式有1为1,合取式有0为0,所以不妨对式子进行赋值,查看式子是否全为1或全为0,还是有1有0来判断是重言式、矛盾式还是可满足式。
如:¬(p→q)∧q∧r
设:q或r为0,则原式为0;p为0,¬(p→q)为0,可推出原式也为0,因此原式为矛盾式。
3.等值演算法
设A,B是两个命题公式,若A,B构成的等价式A↔B为重言式,则称A与B是等值的,记作A⇔B。因此我们只需要通过等值演算判断两个式子是否等值来确定重言式。
例如:

可以看出结果为0,原式为矛盾式。

可以看出结果为p,其中00,01是成假赋值,10,11是成真赋值。
4.主析取范式法
通过求取公式的主析取范式来判断公式类型。
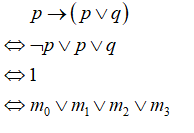
公式等值于1,它的主析取范式包含所有的最小项,因此原式为重言式。

该公式是可满足式,但不是重言式,因为它的主析取范式没含全部8个极小值(2^3=8)。
























 1028
1028

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








