计量经济学及Stata应用陈强第七章异方差习题7.2

最新推荐文章于 2022-12-20 19:42:01 发布

希斯克利

最新推荐文章于 2022-12-20 19:42:01 发布

阅读量1.4w

点赞数 29

文章标签：其他学习方法

本文链接：https://blog.csdn.net/weixin_57956137/article/details/127951195

版权

本文通过BP检验和White检验验证房价回归模型是否存在异方差问题，并利用Stata软件进行实证分析。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

7.2 房价回归是否存在异方差？数据集hprice2a.dta包含美国波士顿506个社区的房屋中位数价格的横截面数据，考虑以下特征价格回归:

$lprice_{i}=\beta _{1}+\beta _{2}lnox_{i}+\beta _{3}ldist_{i}+\beta _{4}rooms_{i}+\beta _{5}stratio_{i}+\varepsilon _{i}$

其中，lprice为房价的对数，lnox为空气污染程度的对数，ldist为社区到就业中心距离的对数，rooms为房屋的平均房间数，stratio为社区学校的学生 - 教师比例，下标i表示社区i。

（1）以5%的置信度，使用BP检验，检验是否存在异方差（假设扰动项为iid，分别以拟合值 $y\hat{}$ 以及所有解释变量进行检验）。

（2）以5%的置信度，使用怀特检验，检验是否存在异方差。

解答如下：

在Stata中导入数据集hprice2a.dta，在命令窗口输入如下命令：

代码：

reg lprice lnox ldist rooms stratio #特征价格回归
rvfplot #画残差与拟合值散点图
estat hettest,iid #使用拟合值y（hat）进行BP检验
estat hettest,iid rhs #使用所有解释变量进行BP检验
estat imtest,white #怀特检验

结果如图：

得到特征价格回归方程： $lprice_{i}=-0.95354lnox_{i}-0.1343401ldist+0.2545271rooms-0.0524512stratio+11.08387$

且各解释变量均显著，不过为初步考察是否存在异方差，画出残差与拟合值的散点图如下：

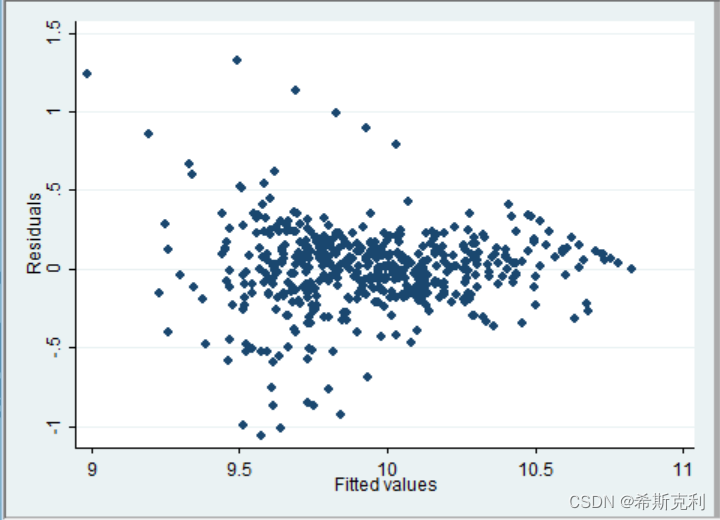
由上图发现当lprice的拟合值较小时，扰动项的方差较大，大致判断可能存在异方差。首先使用拟合值 $y\hat{}$ 进行BP检验结果得P值=0.0000，如下图：

其次使用所有解释变量进行BP检验，结果得P值=0.0000，如下图

综上所述，强烈拒绝同方差的原假设，认为存在异方差，也证实了残差图异方差的大致判断。最后进行5%置信度的White检验，结果得P值（prob>chi2）=0.0000，如下图：

由White检验同样强烈拒绝同方差的原假设，认为存在异方差，其结果与BP检验一致。解决方案请看下一节

计量经济学及Stata应用 陈强 第七章异方差习题7.2

计量经济学及Stata应用陈强第七章异方差习题7.2