算法基础课-第四章数学知识

李加号pluuuus

已于 2023-08-12 22:01:12 修改

阅读量235

点赞数

文章标签：算法

于 2023-08-12 20:59:48 首次发布

本文链接：https://blog.csdn.net/weixin_57974242/article/details/132197424

版权

一、数论

1.1 质数

1.1.1 质数的判定

试除法判定质数

模板题 AcWing 866. 试除法判定质数

给定 n 个正整数 ai，判定每个数是否是质数。

输入格式
第一行包含整数 n。接下来 n 行，每行包含一个正整数 ai。

输出格式
共 n 行，其中第 i 行输出第 i 个正整数 ai 是否为质数，是则输出 Yes，否则输出 No。

数据范围
1≤n≤100,
1≤ai≤231−1

输入样例：
2
2
6
输出样例：
Yes
No

方法1: 直接暴力枚举时间复杂度O(n^2)
但是要求高一点就会超时

bool is_prime(int n)
{
    if(n < 2) return false;
    for(int i=2; i <= n; i++)    
        if(n % i == 0)
            return false;
    return true;
}

优化思路：只需要遍历一半。在找因子时候，只需要遍历根号n部分即可。

方法2：直接使用sqrt函数

bool is_prime(int n){
    if(n < 2) return false; //2是最小的质数，如果n小于2，那n肯定就不是质数
    for(int i = 2;i <= sqrt(n);i ++){ //优化部分
        if(n % i == 0){  //如果可以被i整除，说明这个数不是质数
            return false;  //返回不是
        }
    }
    return true; //返回是
}

但是，这个sqrt 函数底层运行很慢，每次执行这行代码时，需要运算一次，下面看看其他方法

方法3：
将遍历代码优化成：for(int i = 2;i * i <= n;i ++), 本质上跟上面差不多，但是这里可能会出现溢出的风险，不推荐

方法4：
将遍历代码优化成for(int i=2; i <= n / i; i++), 这里不会出现数据溢出的风险，推荐使用

完整代码：

#include <iostream>

using namespace std;

// 试除法
// 将O(n) 降到为 O(sqrt(n))
bool is_prime(int n)
{
    if(n < 2) return false;
    // for(int i=2; i * i <= n; i++)    // 可能有溢出风险
    // for(int i=2; i <= sqrt(n); i++)  // sqrt 函数每次计算，影响效率
    for(int i=2; i <= n / i; i++)   // 只需要判断两个中较小的一个约数就行了
        if(n % i == 0)
            return false;
    return true;
}

int main()
{
    int m;
    cin >> m;
    while(m --)
    {
        int c;
        cin >> c;
        if(is_prime(c)) puts("Yes");
        else puts("No");
    }
    return 0;
}

1.1.2 分解质因数

试除法分解质因数

acwing 867. 分解质因数

给定 n 个正整数 ai，将每个数分解质因数，并按照质因数从小到大的顺序输出每个质因数的底数和指数。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个正整数 ai。

输出格式
对于每个正整数 ai，按照从小到大的顺序输出其分解质因数后，每个质因数的底数和指数，每个底数和指数占一行。

每个正整数的质因数全部输出完毕后，输出一个空行。

数据范围
1≤n≤100, 2≤ai≤2×109

输入样例：
2
6
8
输出样例：
2 1
3 1

2 3

意思是：6 = $2^{1}$ + $3^{1}$ 8 = $2^{3}$

算术基本定理，又称为正整数的唯一分解定理，即：每个大于1的自然数，要么本身就是质数，要么可以写为2个或以上的质数的积，而且这些质因子按大小排列之后，写法仅有一种方式。即：

p1 < p2 < p3 … <pn 均为质数，指数 ai 是正整数

代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

void divide(int n){
	for(int i = 2; i <= n / i; i++){
		if(n % i == 0) {   // i是n的因数 
			int s = 0;       
			while(n % i == 0){
				n /= i;   // i：底数 
				s++;      // s：次数 
			}
			cout << i <<" " << s << endl;
		}
	}
	
	if(n > 1)  cout << n << " 1" << endl;  // n就是大于sqrt(n)的唯一质因子
} 

int main(){
	int n ;
	cin >> n;
	while(n--){
		int a;
		cin >> a;
		divide(a);
	}
	return 0;
}

这里有个性质：n中最多只含有一个大于sqrt(n)的因子。证明通过反证法：如果有两个大于sqrt(n)的因子，那么相乘会大于n，矛盾。对其进行优化：先考虑比sqrt(n)小的，代码和质数的判定类似
最后如果n还是>1，说明这就是大于sqrt(n)的唯一质因子。时间复杂度:O( $\sqrt{n}$ )

朴素算法：如果要寻找11之前的质因数，删掉p之前所有数的倍数。比如2的倍数、3的倍数、4的倍数……删完之后，所有剩下的数就是质数。如果一个数 p 没有被删掉，就说明 p 不是 [ 2, p - 1] 之间任何一个数的倍数。即，[ 2, p - 1] 之间不存在 p 的约数。

时间复杂度：n/2 + n/3 + ... + n/n = n * (1/2 + 1/3 + ... + 1/n ) = O(nlogn)

(n个数中删去2的倍数：n/2 )

优化：只需要删去 [ 2, p - 1] 当中质数的所有倍数。当一个数不是质数的时候，不用删它的倍数。

1.1.3 筛质数

质数：只有1和它本身两个因数（约数），那么这样的数叫做质数。比如7，只有1和7两个约数。

合数：除了能被1和它本身整除，还能被其他的正整数整除，那么这样的数叫做合数。比如8，有1、2、4和8四个约数。

质因子（或质因数）：指能整除给定正整数的质数。根据算术基本定理，不考虑排列顺序的情况下，每个正整数都能够以唯一的方式表示成它的质因数的乘积。

互质：两个没有共同质因子的正整数称为互质。因为1没有质因子，1与任何正整数（包括1本身）都是互质。

质数：只有一个质因子的正整数为质数。

acwing 868. 筛质数

给定一个正整数 n，请你求出 1∼n 中质数的个数。

输入格式
共一行，包含整数 n。

输出格式
共一行，包含一个整数，表示 1∼n 中质数的个数。

数据范围
1≤n≤106

输入样例：
8
输出样例：
4

方法1：朴素版本筛质数：暴力枚举
直接通过枚举1~n 的质数，然后标记一个数的倍数即可
时间复杂度： O(nlogn)

int primes[N], cnt;     // primes[]存储所有素数
bool st[N];         // st[x]存储x是否被筛掉

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (st[i]) continue;
        primes[cnt ++ ] = i;
        for (int j = i + i; j <= n; j += i)
            st[j] = true;
    }
}

过程：

方法2：埃氏筛选法：用质数去筛选合数，但是不能保证每个数筛选了几次
时间复杂度： O(nloglogn)

埃氏筛
定理：一个质数*任何一个不为1的正整数=合数

埃氏筛的基本思想：

假设有一个筛子存放1～N，例如：

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 .........N

先将 2的倍数筛去：

2 3 5 7 9 11 13 15 17 19 21..........N

再将 3的倍数筛去：

2 3 5 7 11 13 17 19..........N

之后，再将5的倍数筛去，再来将7的质数筛去，再来将11的倍数筛去........，如此进行到最后留下的数就都是质数，这就是Eratosthenes筛选方法（Eratosthenes Sieve Method）。

代码：

void get_primes(int n)
{
    for(int i = 2; i <= n; i ++)
    {
        // 只需要筛选质数的倍数就行了
        if(!st[i])
        {
            primes[cnt ++] = i;   // 保存质数
            for(int j = i; j <= n; j += i) //可以用质数就把所有的合数都筛掉；
                st[j] = true;
        }
    }
}

方法3：线性筛选法。核心：保证了每个合数被最小质因子筛选掉。只筛选了一次，所以是线性的
也叫欧拉筛选法。

埃氏筛存在一个缺陷：即对于一个合数，可能会被筛多次。例如 30=2×15=5×6…。改用其最小质因子去筛掉这个合数，就可以保证30只会被筛一次。

从小到大枚举所有质因子 primes[j]。

当出现 i % primes[j] == 0 时，primes[j] 一定是 i 的最小质因子（因为是从小到大枚举），因此也一定是 primes[j] * i 的最小质因子。
当出现 i % primes[j] != 0 时，说明我们还尚未枚举到 i 的任何一个质因子，也就表示 primes[j] 小于 i 的任何一个质因子，这时 primes[j] 就一定是 primes[j] * i 的最小质因子。

可以发现无论如何，primes[j] 都一定是 primes[j] * i 的最小质因子，并且由于所要筛的质数在 2∼n 之间，因此合数最大为 n，故 primes[j] * i 只需枚举到 n 即可，但由于 primes[j] * i 可能会溢出整数范围，故改成 primes[j] <= n / i 的形式。

时间复杂度： O(n)

具体原理参考：线性筛法求素数的原理与实现_太上绝情的博客-CSDN博客

线性筛法，顾名思义，就是在线性时间 O(n) 用筛选的方法把素数找出来的一种算法。确切的说，线性筛法并不是判定素数的，而是在线性时间内求出一个素数表，需要判定是否是素数的时候只要看该数是否在表内就可以瞬间知道是不是素数。比如想求10000以内的素数，定义表int a[10000]，进行线性筛选后，a[n]的值就代表n是不是素数，a[n]==1，n是素数。a[n]==0，n不是素数，这就是查表判定素数，不用再做任何计算。

而如果用遍历取余，那么每判定一个数都要从头开始再遍历一遍，而线性筛法只在开始一次性运算完，以后只要查表即可，查表通常只需要1条语句。所以，如果只需要判定很少几次素数，那么用遍历取余即可，但是如果需要多次判定素数，而且个数还不是很小的话，那么线性筛法就会体现出巨大的优越性来。

线性筛法的核心原理：每个合数必有一个最小质因子（不包括它本身），用这个因子把合数筛掉。证明：合数一定有因子，最小质因子是唯一的，所以合数只会被它自己唯一的因子筛掉一次，把所有合数筛掉后剩下的就全是素数了。

比如：假设一个数 i，一个合数 t ，i 是 t 的最大因数。t 可能并不唯一（例如30和45的最大因数都是15）。如何通过 i 得到 t ？t 必然等于 i 乘一个比 i 小的素数。先来说这个数为什么一定要比 i 小：显然，如果 i 乘上一个比它大的素数，那么 i 显然不能是 t 的最大因子。再来说为什么要是素数：因为如果乘上一个合数，我们知道合数一定可以被分解成几个素数相乘的结果，如果乘上的这个合数x = p1*p2*……，那么t = i * x = i * p1 * p2……很显然p1* i也是一个因数，而且大于 i 。所以必须乘上一个素数。

该乘哪一个比 i 小的素数呢？先给出结论：任意一个数 i = p1*p2*……*pn，p1、p2、…、pn都是素数，则p1是其中最小的素数，设T = i * M（显然T就成了一个合数），那么 T 的最大因数就是i。乘上的数要 <= i 的最小质因数。

从小到大枚举每个数

1.如果当前数没划掉，必定是质数，记录该质数

2.枚举已记录的质数 (如果合数已越界则中断)

(1) 合数未越界，则划掉合数

(2)条件 i%p==0，保证合数只被最小质因子划掉

若 i 是质数，则最多枚举到 primes[j] 自身中断
若 i 是合数，则最多枚举到自身的最小质数primes[j]中断

模板：

int primes[N], cnt;     // primes[]存储所有素数
bool st[N];         // st[x]存储x是否被筛掉

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;  // 如果当前数没划掉，必定是质数，记录该质数
        for (int j = 0; primes[j] <= n / i; j ++ ) // 枚举已记录的质数
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;  // 保证合数只被最小质因子划掉
        }
    }
}

只有上一刻的我能看懂的过程：

代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e6 + 10;
bool st[N];
int primes[N], cnt;

// 朴素版本筛质数
void get_primes(int n)
{
    for(int i = 2; i <= n; i ++)
    {
        if(!st[i]) primes[cnt ++] = i;  // 保存质数
        for(int j = i; j <= n; j += i)  // 删除质数的倍数
            st[j] = true;
    }
}

// 埃氏筛选法： 用质数去筛选合数，但是不能保证每个数筛选了几次
void get_primes2(int n)
{
    for(int i = 2; i <= n; i ++)
    {
        // 只需要筛选质数的倍数就行了
        if(!st[i])
        {
            primes[cnt ++] = i;   // 保存质数
            for(int j = i; j <= n; j += i) //可以用质数就把所有的合数都筛掉；
                st[j] = true;
        }
    }
}


// 线性筛选法：保证了每个合数被最小质因子筛选出来的，只筛选了一次，所以是线性的 
void get_primes3(int n)
{
    for(int i = 2; i <= n; i ++)
    {
        // 如果不是质数， 加入进去
        if(!st[i]) primes[cnt ++] = i;  // 保存质数
        // 这个筛法：是从小到大枚举所有的质数
        for(int j = 0; primes[j] <= n / i; j ++)
        {
            // 表示用primes[j] * i的最小质因数primes[j] 筛掉primes[j] * i这个合数
            // 因为此时i % primes[j] == 0一定是未成立的，因此primes[j]一定小于i的最小质因数，因此primes[j]是primes[j]*i的最小质因数
            st[primes[j] * i] = true;

			// 因为此时i % primes[j] == 0成立了，primes[j]是i的最小质因数。
			// 如果此时不break，那么primes[j]会继续向后遍历，导致primes[j]不再是i的最小质因数，也不是primes[j] * i的最小质因数
            if(i % primes[j] == 0) break;   // primes[j] 一定是i 的最小质因子
        }
    }
}

int main()
{
    int n;
    cin >> n;
    get_primes3(n);
    cout << cnt << endl;
    return 0;
}

1.2 约数

约数，又称因数。若a / b == 0, 整数a除以整数b除得的商正好是整数而没有余数，我们就说a能被b整除，或b能整除a。a称为b的倍数，b称为a的约数。可以理解为除数。

如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数： (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和： (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)

1.2.1 试除法求约数

acwing 869. 试除法求约数

给定 n 个正整数 ai，对于每个整数 ai，请你按照从小到大的顺序输出它的所有约数。

输入格式
第一行包含整数 n。接下来 n 行，每行包含一个整数 ai。

输出格式
输出共 n 行，其中第 i 行输出第 i 个整数 ai 的所有约数。

数据范围
1≤n≤100, 2≤ai≤2×109

输入样例：
2
6
8
输出样例：
1 2 3 6
1 2 4 8

思路：枚举1~n， d * d <= n，只需要遍历根号n部分即可

注意数论问题一定要注意时间复杂度。

考虑到：约数个数数量多少不定，且需要排序，所以用vector数组

代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

vector<int> get_divisors(int n)
{
    vector<int> re;
    for(int i =1; i <= n / i; i ++)
        if(n % i == 0)
        {
            re.push_back(i);
            if(i != n / i) re.push_back(n / i);   // 防止完全平方数，约数是中间部分
        }
    sort(re.begin(), re.end());
    return re;
}

int main()
{
    int n;
    cin >> n;
    while (n -- )
    {
        int a;
        cin >> a;
        auto v = get_divisors(a);
        
        for(auto &t : v)
            cout << t << ' ';
        cout << endl;
    }
    return 0;
}

比如 6 = 2 * 3，先遍历到2，re.push_back(2)，再判断是不是完全平方数，不是的话加入另一个乘数。re.push_back(6 / 2)。一次循环加入两个数。完全平方数比如12 * 12 = 144，避免加入重复数字。

1.2.2 约数个数

举例：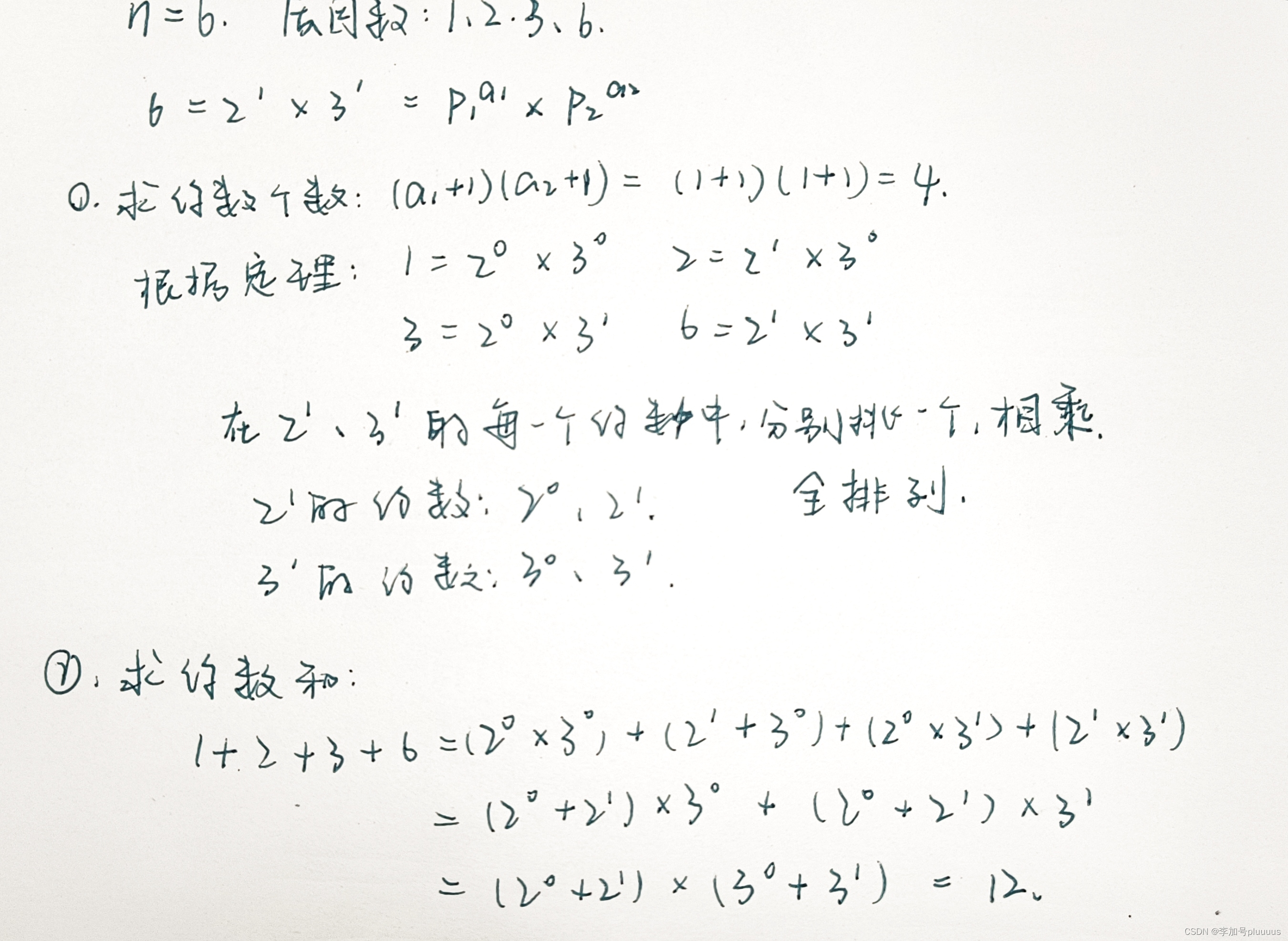

约数个数定理

在这里插入图片描述

注：int范围内约数个数最多的一个数，它的约数是1500个左右。

例题

AcWing 870. 约数个数

给定 n 个正整数 ai，请你输出这些数的乘积的约数个数。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个整数 ai。

输出格式
输出一个整数，表示所给正整数的乘积的约数个数，答案需对 10^9+7 取模。

数据范围
1≤n≤100,
1≤ai≤2×10^9

输入样例：
3
2
6
8
输出样例：
12

先用公式笔算一下：2 * 6 * 8 = $(2^1) * (2^1 * 3^1) * (2^3)$ = $2^{5} * 3^{1}$ ，用各个质数的指数+1后再相乘，即为此数的约数个数，即为 (5 + 1)(1 + 1) = 6 * 2 = 12

思路：先把原数分解为质因数，最后把每一个数的指数+1后再相乘即可。由于a过大，此处用哈希表进行存储。哈希表 first 存储底数， second 存储指数。

代码：

#include <iostream>
#include <cstring>
#include <unordered_map>

using namespace std;

typedef long long LL;

const int mod = 1e9 + 7;

int main(){
	int n;
	cin >> n;
	
	unordered_map<int, int> prime;
	
	while(n--){
		int x;
		cin >> x;
		for(int i = 2; i <= x/i; i++){
			while(x % i == 0){
				x = x/i;      
				prime[i]++;   // 键：底数x，值：指数 
			}
		}
		if(x > 1) prime[x] ++;  // 大于 x/i 的质因子
	}
	
	LL res = 1;
	for(auto t : prime) res = res * (t.second + 1);
	cout << res <<endl;
	return 0; 
}

unordered_map 容器：和 map 容器仅有一点不同，即 map 容器中存储的数据是有序的，而 unordered_map 容器中是无序的。以键值对（pair类型）的形式存储数据，存储的各个键值对的键互不相同，且不允许被修改。由于 unordered_map 容器底层采用的是哈希表存储结构，该结构本身不具有对数据的排序功能，所以此容器内部不会自行对存储的键值对进行排序。
unordered_map 容器在<unordered_map>头文件中。

1.2.3 约数之和

约数和定理

直接走度娘：约数和定理_百度百科 (baidu.com)

证明：

比如：

例题：正整数360的所有正约数的和是多少？

解：将360分解质因数可得 360= $2^{3} * 3^{2} * 5^{1}$

由约数和定理可知，360所有正约数的和为

( $2^{0} + 2^{1} + 2^{2} + 2^{3}$ ) × ( $3^0+3^1+3^2$ ) × ( $5^0+5^1$ ) = (1+2+4+8) × (1+3+9) × (1+5)

= 15 × 13 × 6 = 1170

例题

AcWing 871. 约数之和

给定 n 个正整数 ai，请你输出这些数的乘积的约数之和，答案对 109+7 取模。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个整数 ai。

输出格式
输出一个整数，表示所给正整数的乘积的约数之和，答案需对 109+7 取模。

数据范围
1≤n≤100,
1≤ai≤2×109
输入样例：
3
2
6
8
输出样例：
252

思路：

1、在每次输入一个数时，分解其质因数，将其出现的次数保存起来；
2、遍历保存质因数的表，将每个质因数带入公式中。

这里的代码实现存储底数和指数部分跟上一题约数个数一样，只是求解目标变了

#include <iostream>
#include <cstring>
#include <unordered_map>

using namespace std;

typedef long long LL;

const int mod = 1e9 + 7;

int main(){
	int n;
	cin >> n;
	
	unordered_map<int, int> prime;
	
	while(n--){
		int x;
		cin >> x;
		for(int i = 2; i <= x/i; i++){
			while(x % i == 0){
				x = x/i;      
				prime[i]++;   // 键：底数x，值：指数 
			}
		}
		if(x > 1) prime[x] ++;  // 大于 x/i 的质因子
	}
	
	// 和计算约数个数的过程一致。下面是求和过程，也是根据公式 
	
	LL res = 1;
	for(auto p : prime){
		int a = p.first, b = p.second;
		int t = 1;
		
		while(b--)                
			t = (t * a + 1) % mod;  // 求和公式：p^0 + p^1 +...+ p^n   
		
		res = (res * t) % mod;
	}
	cout << res <<endl;
	return 0; 
}

秦九韶算法求多项式的值：

while(a- -) t = ( t * p + 1 ) % mod;
循环第一次：t = p^1 + p^0
循环第二次：t = p^2 + p^1 + p^0
循环第三次：t = p^3 + p^2 + p^1 + p^0
循环第 a 次：t = p^0 + p^1 + p^2 + … + p^a

秦九韶算法：快速计算多项式的值 - 知乎 (zhihu.com)

Horner法则（秦九韶算法）的程序实现_秦九韶算法程序_远在远方的风比远方更远的博客-CSDN博客

1.2.4 最大公约数 ☆

头文件：gcd函数在numeric头文件中（有的编译软件会显示不可以）, 也可用万能头文件bits/stdc++.h声明。

万能头文件 #include <bits/stdc++.h> 是C++中支持的一个几乎万能的头文件，几乎包含所有的可用到的C++库函数。以后写代码就可以直接引用这一个头文件了，不需要在写一大堆vector、string、map、stack……

欧几里得算法：

即辗转相除法，是指用于计算两个非负整数a，b的最大公约数。

计算公式gcd(a,b) = gcd(b , a mod b)。

依据一个基本性质：d | a，d | b，d | (a+b)，d | (ax + by)
（d能整除a，d能整除b，那么d就能整除a+b，也能整除a的若干倍+b的若干倍）

递归代码，出口条件是b==0,否则则让a=b; b=a%b;一直递归下去直到满足出口条件.

代码模板，或者说原理：

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

举例：

举例：假如需要求 1997 和 615 两个正整数的最大公约数,用欧几里德算法，是这样进行的：

1997 / 615 = 3 (余 152)
615 / 152 = 4(余7)
152 / 7 = 21(余5)
7 / 5 = 1 (余2)
5 / 2 = 2 (余1)
2 / 1 = 2 (余0)
至此，最大公约数为1
以除数和余数反复做除法运算，当余数为 0 时，取当前算式除数为最大公约数，所以就得出了 1997 和 615 的最大公约数 1

数学推导：欧几里得算法详解_辜月的博客-CSDN博客

例题

AcWing 872. 最大公约数

给定 n 对正整数 ai,bi，请你求出每对数的最大公约数。

输入格式
第一行包含整数 n。接下来 n 行，每行包含一个整数对 ai,bi。

输出格式
输出共 n 行，每行输出一个整数对的最大公约数。

数据范围 1≤n≤105,1≤ai,bi≤2×109

输入样例：
2
3 6
4 6
输出样例：
3
2

代码：

#include <iostream>

using namespace std;

int gcd(int a, int b)   // 欧几里得算法
{
    return b ? gcd(b, a % b) : a;
}

int main()
{
    int n;
    cin >> n;
    while (n -- )
    {
        int x, y;
        cin >> x >> y;
        int re = gcd(x, y);
        cout << re << endl;
    }
    return 0;
}

扩展欧几里得算法：

// 求x, y，使得ax + by = gcd(a, b)
int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1; y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y -= (a/b) * x;
    return d;
}

1.2.5 欧拉函数

欧拉函数定义：小于 x 的整数中与 x 互质的数的个数，一般用φ(x)表示。特殊的，φ(1)=1。

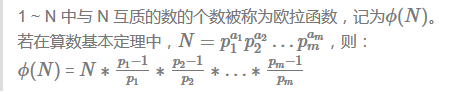
互质的定义：互质是公约数只有1的两个整数，叫做互质整数。特别的，1与任何整数都互质。比如n=6，则与6互质的数有1和5。根据欧拉函数计算：6的质因子有2和3，6*(1-1/2)*(1-1/3) = 2。即前N个数中与N互质数的个数。

对于质数来说，欧拉函数值就是其本身减去1。根据质数的定义，只包含1和本身两个约数。比如质数7，与1~6都互质。

证明：

首先要引入容斥原理：在计数时，必须注意没有重复，没有遗漏。为了使重叠部分不被重复计算，基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

比如概率论中求P（A+B+C）的概率就是P（A+B+C）= P(A) + P(B) + P(C) - P(AB) - P(AC) - P(BC) + P(ABC)。

先包含：P(A) + P(B) + P(C)

再排斥：- P(AB) - P(AC) - P(BC) + P(ABC)

同理，要求前N个数中与N互质的数的个数，首先找出N的质因子p1,p2,...,pk。1~N中，N的质因子及其倍数一定不与N互质，所以要先 N -（N / p1 + N / p2 +... +N / pk），N / pi是 1 到 N 中 pi 的倍数个数。同时，一个数既可能是pi的倍数也可能是pj的倍数，这样便重复减了，还需要加上（N / p1p2 + N / p1p3 +...+N / p1pk +N / p2p3 + ... + N / pk-1pk），然后根据容斥原理，后面还要加上三个数公共倍数的个数，减去四个数公共倍数的个数。将欧拉函数的式子N(1-1/p1)...(1-1/pk)展开就可以得到该前面的展开式了。为了避免出现小数，在编程时将1 - 1 / pi会写成乘上pi - 1再除以pi。

具体的数学解释请看：浅谈欧拉函数_liuzibujian的博客-CSDN博客

（臣妾是真的看不懂啊）（只能背公式了呜呜呜）

例题

AcWing 873 欧拉函数

题目描述：

给定n个正整数ai，请你求出每个数的欧拉函数。

输入格式

第一行包含整数n。接下来n行，每行包含一个正整数ai。

输出格式

输出共n行，每行输出一个正整数ai的欧拉函数。

数据范围

1≤n≤100,1≤ai≤2∗10^9

输入样例：

3
3
6
8
输出样例：

2
2
4

先想一下：与3互质的数有2个：1、2。与6互质的数有2个：1、5。与8互质的数有4个：1、3、5、7。想要求φ(6)，直接套公式：φ(6) = 6 × $\frac{2-1}{2}$ × $\frac{3-1}{3}$ = 2.

代码可以套用分解质因数的代码：

#include <iostream>
using namespace std;

int euler(int x) {
  int res = x;
  for (int i = 2; i <= x / i; i++) {
    if (x % i == 0) {
      // 这里i是x的素因子，所以可以先除再乘
      res = res / i * (i - 1);
      while (x % i == 0) x /= i;
    }
  }

  if (x >= 2) res = res / x * (x - 1);
  return res;
}

int main() {
  int n;
  cin >> n;
  while (n--) {
    int a;
    cin >> a;
    cout << euler(a) << endl;
  }
}

（rnm，太抽象了）

通过遍历2到sqrt(x)之间的数 i ，找出 x 的所有因子，并更新结果 res。当找到一个因子 i 时，将 res 乘以 $\frac{i - 1}{i}$ 。这样做的目的是每次找到一个因子 i 时，将之前已经遍历过的因子对 res 的贡献进行逆操作，即将之前的贡献减少。而对于新的因子 i，我们将其贡献加上。
例如，假设a = 12，当前循环到的因子i = 2，则执行 res = res / i * (i - 1) 的计算：当前的 res 为12，i 为2，所以计算结果为 res = 12 / 2 * (2 - 1) = 6。
这样，通过每次将res × $\frac{i - 1}{i}$ 的方式，我们可以保持res为之前所有因子对结果的贡献的累积。
while循环，令 x 不断除以 i ，直到 x 不能再被 i 整除为止。目的是找到质因子的底数 pi。最后，如果 x 大于1，那么说明 x 是一个大于sqrt(a)的质数。因为在循环中已经遍历了2到sqrt(a)之间的所有可能的因子，如果 x 还大于1，说明它没有被任何小于等于sqrt(a)的数整除，因此 x 是一个质数。将res更新为 res × $\frac{x - 1}{x}$ ，即欧拉函数的计算方式。得到的结果即为 x 的欧拉函数值。

例题

AcWing 874. 筛法求欧拉函数（线性筛）

给定一个正整数 n，求 1∼n 中每个数的欧拉函数之和。

输入格式
共一行，包含一个整数 n。

输出格式
共一行，包含一个整数，表示 1∼n 中每个数的欧拉函数之和。

数据范围
1≤n≤106
输入样例：
6
输出样例：
12

先想一下：φ(1) = 1，φ(2) = 1，φ(3) = 2，φ(4) = 2，φ(5) = 4，φ(6) = 2，总和=12

思路：因为这个题n的数据量很大，所以我们需要用线性筛，线性筛质数的过程中，顺便求出每个数的欧拉函数值，然后累加。

过程：

1）质数 i 的欧拉函数即为：phi[i] = i - 1。因为1 ~ i−1均与 i 互质，共i−1个。

2） phi[primes[j] * i ] 分为两种情况：

i % primes[j] == 0：primes[j] 是 i 的最小质因子，也是 primes[j] * i 的最小质因子，因此1 - 1 / primes[j] 这一项在 phi[i] 中计算过了，只需将基数N修正为 primes[j] 倍，最终结果为 phi[i] * primes[j]。
i % primes[j] != 0：primes[j]不是 i 的质因子，只是 primes[j] * i 的最小质因子，因此不仅需要将基数N修正为primes[j]倍，还需要乘上 $\frac{primes[j]-1}{primes[j]}$ 这一项，因此最终结果为 phi[i] * (primes[j] - 1

举例说明：

第一种情况，比如 i = 6, p[j] = 2，i % p[j] == 0。 2是 i = 6 的最小质因子，也是12的最小质因子。φ(i × p[j]) = φ(i) × p[j] 。φ(6 × 2) = φ(6) × 2 = 4。12的欧拉值有1、5、7、11.
第二种情况，比如 i = 3, p[j] = 2，i % p[j] != 0。2是 i × p[j] = 6 的最小质因子，φ(i × p[j]) = φ(i) × (p[j] - 1) 。代入得 φ(3 × 2) = φ(6) = φ(3) × (2-1) = 2 × 1 = 2

代码：

#include <iostream>
using namespace std;

const int N = 100010;
int prime[N], cnt;
int phi[N];
bool st[N];
typedef long long LL;

int get_eulers(int n){   // 线性筛质数 

    phi[1] = 1; // 根据定义，别漏了！ 
    
	for(int i = 2; i <= n; i++){
		if(!st[i]) {     //  i没被筛掉，是质数 
			prime[cnt++] = i;
			phi[i] = i - 1;   // 质数 i 的欧拉值是 i-1 
		}
		
		for(int j = 0; prime[j] <= n / i; j++){  // 枚举已保存的所有质数 
			st[prime[j] * i] = true;             // 筛掉合数  primes[j] * i 
			 
			 // 相较于线性筛，补充的部分 
			if(i % prime[j] == 0) {              // prime[j]是 i的最小质数
				phi[prime[j] * i] = phi[i] * prime[j];  // 套公式 
			    break;      
			} 
			
            phi[prime[j] * i] = phi[i] * (prime[j] - 1);  // i % primes[j] != 0 ,prime[j]是 i * prime[j] 的最小质数，套公式
			
		}
	}
	    LL res = 0;
    for(int i=1; i<=n; ++i){
        res += phi[i];
    }
    return res;
}

int main(){
	int n;
	cin >> n ;
	cout << get_eulers(n) << endl;
	return 0;
}

欧拉定理：

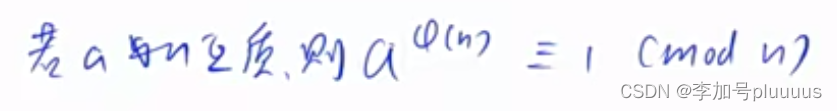
1.3 快速幂

就是更快速的计算幂运算。
比如计算a^b。幂运算有现成的公式，可以直接pow（a,b）。时间复杂度是O(b)，即每次乘b，都得再运算一次。如果b的值很大，那么代码的运行时间会很长，很多题目会疯狂时间超限。
而快速幂算法的时间复杂度是O（logb），可以有效减少运行计算机计算的次数。

应用：求逆元，但必须是质数。即扩展欧几里得算法。

d一定会是 a和b的最大公约数的倍数。

快速幂:快速求 $a^{b}$ % p的问题,时间复杂度:O(logb)。若对于n组数据,那么时间复杂度为O(n∗logb)

以下转自：快速幂算法（C++）_快速幂c++代码_L-M-Y的博客-CSDN博客

例子：
计算2^32（a=2,b=32）
2*2=2^2;
2^2 *2^2 =2^4;
2^4 *2^4 =2^8;
2^8 *2^8 =2^16;
2^16 *2^16 =2^32;
时间复杂度优化为O（log32）。可以认为，这个算法基于倍增原理，与其每次逐个乘，不如每次将a的值翻倍。

当b是2的整数幂时，计算很简单，可是若b不是2的整数幂时该怎么办呢？

例子：
计算5^105。虽然105不是2的幂，但是我们可以把它写成2的幂的和。
105 = 1 + 8 + 32 + 64 = 2^0 + 2^3 + 2^5 + 2^6
算法的关键：把b分解为2的幂之和可以二进制的角度来分解这个问题。

首先，105，1, 8，32，64这5个数的二进制表示：

在这里插入图片描述

很明显，105每个二进制位中的1和下面的数的二进制位中的1是一一对应的。通过这种方式，将b分解为2的幂的和。

伪代码：

fun(int a,int b){
	
	int sum = 1;
	 
    while(b!=0){
    	
	    if( b%2 == 1){
	        sum = sum*a;
			a = a * a;
			b >>= 2； 
		}
	}
}

从b的初始值开始，对b的每一个二进制位进行遍历，如果该位等于一，则让sum乘以a

在这里插入图片描述

一.暴力解法 O(n∗b)，会超时

基本思路:对于n组数据,分别循环b次求出 $a^{b}$ % p

#include<iostream>
using namespace std;
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a,b,p;
        long long res=1;
        cin>>a>>b>>p;
        while(b--)
            res = res * a %p;
        cout<<res<<endl;
    }
}

二.快速幂解法 O(n∗logb)

快速幂迭代版

#include<iostream>
using namespace std;
long long qmi(long long a,int b,int p)
{
    long long res=1;
    while(b)//对b进行二进制化,从低位到高位
    {
        //如果b的二进制表示的第0位为1,则乘上当前的a
        if(b&1) res = res *a %p;
        //b右移一位
        b>>=1;
        //更新a,a依次为a^{2^0},a^{2^1},a^{2^2},....,a^{2^logb}
        a=a*a%p;
    }
    return res;
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        cin.tie(0);
        ios::sync_with_stdio(false);
        int a,b,p;
        long long res=1;
        cin>>a>>b>>p;
        res = qmi(a,b,p);
        cout<<res<<endl;
    }
    return 0;
}

快速幂递归版

#include<iostream>
using namespace std;
#define ull unsigned long long
ull quick_pow(ull a,ull b,ull p)
{
    if(b==0) return 1;
    a%=p;
    ull res=quick_pow(a,b>>1,p);
    if(b&1) return res*res%p*a%p;
    return res*res%p;
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a,b,p;
        cin.tie(0);
        ios::sync_with_stdio(false);
        cin>>a>>b>>p;
        cout<<quick_pow(a,b,p)<<endl;
    }
    return 0;
}

解释：快速幂算法（C++）_快速幂c++代码_L-M-Y的博客-CSDN博客

AcWing 876. 快速幂、扩展欧几里得求逆元（乘法逆元，费马小定理）

二、组合计数

例题

AcWing 885. 求组合数 I（递推）

题解转自：AcWing 887. 求组合数 III（Lucas定理+优化版）_lucasyls_Brightess的博客-CSDN博客

组合数模板一：O(n^2)

QQ图片20220128001520.png

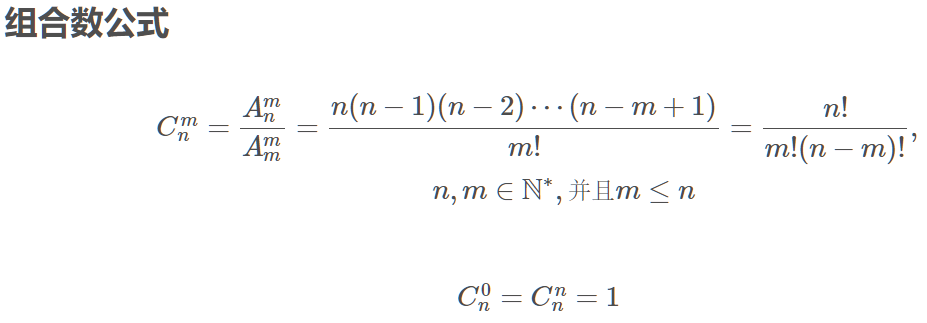
QQ图片20220127194743.png

题型:给定两个正整数a与b,求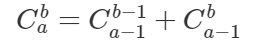： QQ图片20220127180018.png

递推式：直接预处理出c[a][b]所有的值。

公式求组合数时间复杂度 O(n^2)，主要是有预处理的两重循环。本题复杂度准确来说是O(n^2+m)， m是表示m次询问，但是m可以忽略不计，所以本题时间复杂度大约是2000^2=4e6，在合法的范围内。

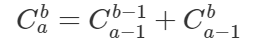
QQ图片20220127175305.png

关键：找出递推关系c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod

#include<bits/stdc++.h>

using namespace std;

const int N = 2020,mod = 1e9+7;
int n;
int c[N][N];
int a,b;

void init(){

    for(int i=0;i<N;++i){
        for(int j=0;j<=i;++j){

            if(!j) c[i][j]=1;//注意c[0][0]，c[1][0]，c[2][0]......的值都是0
            else c[i][j] = (c[i-1][j] + c[i-1][j-1])%mod;
        }
    }
}


int main(){

    init();
    cin>>n;
    while(n--){

        cin>>a>>b;
        cout<<c[a][b]<<endl;
    }
    
    return 0;
}

记忆化搜索写法：

#include<bits/stdc++.h>

using namespace std;


typedef long long LL;
const int N = 2010;
const int mod = 1e9+7;

// 第二种写法，保存之前计算过的每个值到res数组中
int res[N][N];
LL comb(int n, int m)
{
    if (m == 0 || m == n)
        return 1;
    if (res[n][m] != 0)
        return res[n][m];
    return res[n][m] = (comb(n - 1, m) + comb(n - 1, m - 1)) % mod;
}

int main()
{
    init();
    int n;
    cin>>n;
    while(n--)
    {
        int a, b;
        cin>>a>>b;
        cout<<comb(a, b)<<endl; // 第一种提交方式

    }
}

AcWing 886. 求组合数 II（预处理+优化的O(n)版本）

题目同上。组合数模板二：O(a*log(mod))（a–组合数下界，mod–模数）

QQ图片20220127205441.png

QQ图片20220127205313.png

与组合数I不同的是，上一题是预处理所有c[a][b]的值，这一题是预处理中间的一步

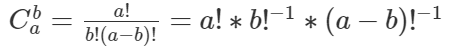
QQ图片20220127195535.png

(b!)^(−1) 与 ((a−b)!)^(−1) 该如何求呢？

答案：利用之前学过的利用快速幂求逆元

时间复杂度：O(a∗log(mod))（a 是组合数的下界，求逆元的时候快速幂的时间复杂度是 log mod，此时 mod-2 就是几次幂）

//关键在预处理

#include<bits/stdc++.h>

using namespace std;

#define int long long
const int mod=1e9+7,N=1e5+10;
int fac[N],infac[N];

int qmi(int a, int k, int p)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = res * a % p;
        a = a * a % p;
        k >>= 1;
    }
    return res;
}

signed main()
{
    int n;
    fac[0]=infac[0]=1;
    for(int i=1;i<N;i++)
    {
        //存阶乘 mod p 的值
        fac[i]=fac[i-1]*i%mod;
        
        //存阶乘的逆元 mod p 的值，利用了上方推到的递推式
        infac[i]=infac[i - 1] * qmi(i,mod-2,mod)%mod;
    }
    
    cin>>n;
    while(n--)
    {
        int a,b;
        cin>>a>>b;
        cout<<fac[a] * infac[b] % mod * infac[a - b] % mod<<endl;
        //注意这里是三个相乘，容易溢出long long，因此两个数乘完后要及时mod，末尾也要mod
    }
}

优化版本：（47 ms）

时间复杂度：O(a)（a 是组合数的下界）

由于在上方的原版代码中，我们预处理两个数组都是正向来求解，我们可以以另一种方式思考：将infac数组的预处理逆向操作，这样做的话，我们可以节省每次循环都要进行一次快速幂求逆元（alog mod）的时间，优化为：只在初始时进行仅仅一次快速幂，这样就大大降低了时间复杂度。使之优化成了线性（O(a)）

代码：

#pragma GCC optimize(2)
#include<bits/stdc++.h>

using namespace std;
#define int long long
const int mod = 1e9+7,N = 1e5+10;
int n;
int fac[N],infac[N];
int a,b;

inline int qmi(int a,int b)
{
    int res = 1;
    while(b)
    {
        if(b&1) res = res * a % mod;
        b>>=1;
        a = a * a % mod;
    }
    return res;
}

inline void init()
{
    fac[0] = infac[0] = 1;
    for(int i=1;i<N;++i) fac[i] = fac[i-1] * i % mod;
    infac[N-1] = qmi(fac[N-1],mod-2);
    for(int i=N-2;i>=1;--i)
    {
        infac[i] = infac[i+1] * (i+1) % mod;//将推出来的递推公式变一下形
    }
}

signed main()
{
    init();
    scanf("%lld",&n);
    while(n--)
    {
        scanf("%lld%lld",&a,&b);
        printf("%lld\n",fac[a]*infac[b]%mod*infac[a-b]%mod);
    }

    return 0;
}

AcWing 887. 求组合数 III（Lucas定理+优化版）

在这里插入图片描述

在这里插入图片描述组合数模板三：O(plog{2,n})，本题还要在此基础上乘最多20组测试数据

QQ图片20220127235025.png

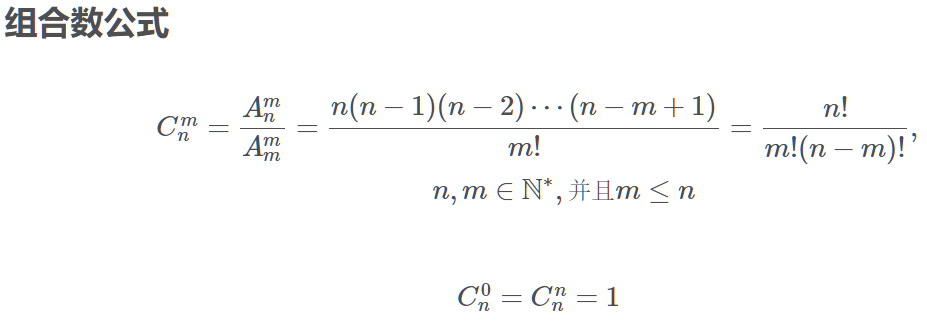
109146_0f48089e7f-QQ图片20220127194743.png

解决核心：卢卡斯定理

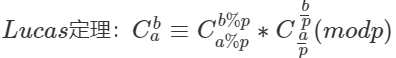
QQ图片20220127235447.png

QQ图片20220128111042.png

写法一：优化之处在于把原本每次for循环都要qmi求的逆元优化到最后一步返回值的时候来求解（是对于C函数的改编）

#include<bits/stdc++.h>

using namespace std;

#define int long long

int qmi(int a,int k,int p)
{
    int res = 1;
    while(k)
    {
        if(k&1) res = res*a%p;
        a = a*a%p;
        k>>=1;
    }
    return res;
}

int C(int a, int b, int p)
{
    if(a < b) return 0;
    
    int down = 1, up = 1;
    for(int i=a, j=1; j<=b; i--, j++)
    {
        up = up * i % p;
        down = down * j % p;
    }

    return up * qmi(down, p-2, p) % p;//其实优化之处就是把原本每次for循环都要qmi求的逆元优化到最后一步返回值的时候来求解
}

int lucas(int a,int b,int p)//lucas定理，套公式即可
{
    if(a<p && b<p) return C(a,b,p);//这一步从定义出发计算即可
    return C(a%p,b%p,p)*lucas(a/p,b/p,p)%p;
    //a%p后肯定是<p的,所以可以用C(),但a/p后不一定<p 所以用lucas继续递归
}

signed main()
{
    int n;
    cin >> n;
    while(n--)
    {
        int a,b;
        int p;
        cin >> a >> b >> p;
        cout << lucas(a,b,p) << endl;
    }
    return 0;
}

写法二：

#include<bits/stdc++.h>

using namespace std;

#define int long long

int qmi(int a,int k,int p)
{
    int res = 1;
    while(k)
    {
        if(k&1) res = res*a%p;
        a = a*a%p;
        k>>=1;
    }
    return res;
}

int C(int a,int b,int p)//从定义出发来编写的函数
{
    int res = 1;
    for(int i=1,j=a;i<=b;i++,j--)
    {
        res = res*j%p;//乘分子：a * (a-1) * .... * (a-b+1)
        res = res*qmi(i,p-2,p)%p;//除分母：原本是除上i，这里要转为乘上i的逆元，逆元结合费马小定理用快速幂来计算
    }
    return res;
}

int lucas(int a,int b,int p)//lucas定理，套公式即可
{
    if(a<p && b<p) return C(a,b,p);//这一步从定义出发计算即可
    return C(a%p,b%p,p)*lucas(a/p,b/p,p)%p;//a%p后肯定是<p的,所以可以用C(),但a/p后不一定<p 所以用lucas继续递归
}

signed main()
{
    int n;
    cin >> n;
    while(n--)
    {
        int a,b;
        int p;
        cin >> a >> b >> p;
        cout << lucas(a,b,p) << endl;
    }
    return 0;
}

分解质因数法求组合数 —— 模板题 AcWing 888. 求组合数 IV

当我们需要求出组合数的真实值，而非对某个数的余数时，分解质因数的方式比较好用：
    1. 筛法求出范围内的所有质数
    2. 通过 C(a, b) = a! / b! / (a - b)! 这个公式求出每个质因子的次数。 n! 中p的次数是 n / p + n / p^2 + n / p^3 + ...
    3. 用高精度乘法将所有质因子相乘

int primes[N], cnt;     // 存储所有质数
int sum[N];     // 存储每个质数的次数
bool st[N];     // 存储每个数是否已被筛掉


void get_primes(int n)      // 线性筛法求素数
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}


int get(int n, int p)       // 求n！中的次数
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}


vector<int> mul(vector<int> a, int b)       // 高精度乘低精度模板
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }

    while (t)
    {
        c.push_back(t % 10);
        t /= 10;
    }

    return c;
}

get_primes(a);  // 预处理范围内的所有质数

for (int i = 0; i < cnt; i ++ )     // 求每个质因数的次数
{
    int p = primes[i];
    sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}

vector<int> res;
res.push_back(1);

for (int i = 0; i < cnt; i ++ )     // 用高精度乘法将所有质因子相乘
    for (int j = 0; j < sum[i]; j ++ )
        res = mul(res, primes[i]);

题解转自：AcWing 889. 满足条件的01序列 - AcWing

AcWing 889. 满足条件的01序列（卡特兰组合数，快速幂/扩欧/优化版预处理求逆元）

题目描述
给定 n 个 0 和 n 个 1，它们将按照某种顺序排成长度为 2n 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。

输出的答案对 1e9+7取模。

输入格式
共一行，包含整数 n。

输出格式
共一行，包含一个整数，表示答案。

数据范围
1≤n≤10^5
样例
输入样例：
3
输出样例：
5

举例：

三个0，三个1。如果要求满足题目条件，则第一个数必须是0，最后一个数必须是1

0 0 0 1 1 1
0 0 1 1 0 1
0 0 1 0 1 1
0 1 0 0 1 1
0 1 0 1 0 1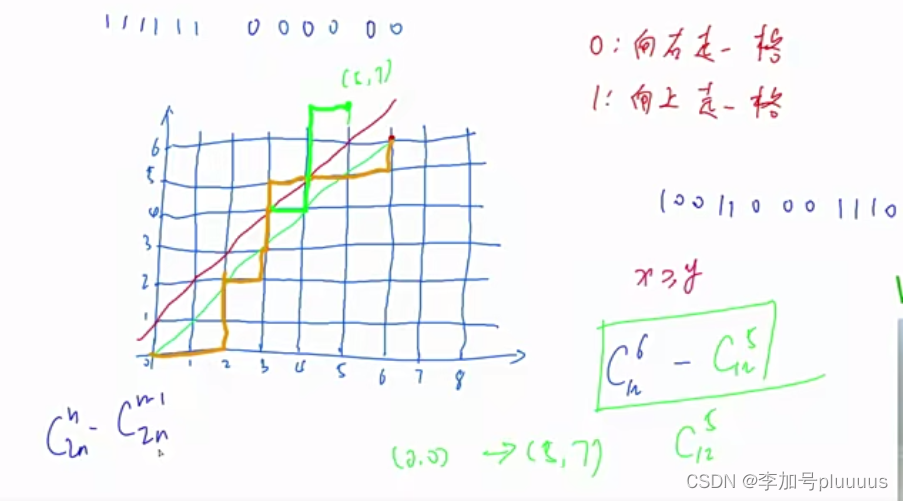

总方案数： $c_{12}^{5}$ 。总共向右走5步，向上走7步，共12步，其中5步是向右走的。

题目分析：

如果n等于6，即6个0和6个1，可将题目转化为从原点（0，0）走到终点（6，6）有多少路径的问题。即把每一种数列转化成一种路径。

0：向右走一格
1：向上走一格

可以把任何一个排列转化成从（0，0）走到（6，6）的路径，任何一条从（0，0）走到（6，6）的路径都可以转化成一个排列。需要满足：任意前缀序列的 0 的个数都不少于 1 的个数，则 x>=y。路径必须在对角线以下。即满足条件的路径都不能超过蓝边（可以经过蓝边但是绝对不能经过红边）

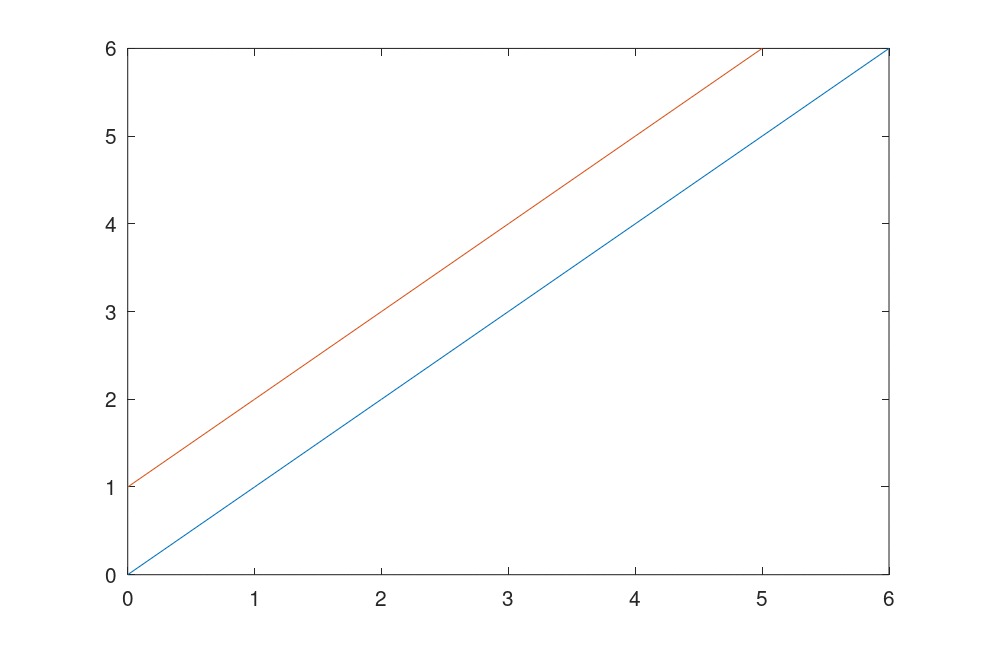
那么问题转化为：从（0，0）到（n，n）不经过红边的所有路径个数：即总共的方案数 - 经过红边的方案数。总方案数： $C_{2n}^{n}$ 。

经过红颜色边的路径个数：

案例: 0 0 1 1 0 1 1 1 0 0 0 1

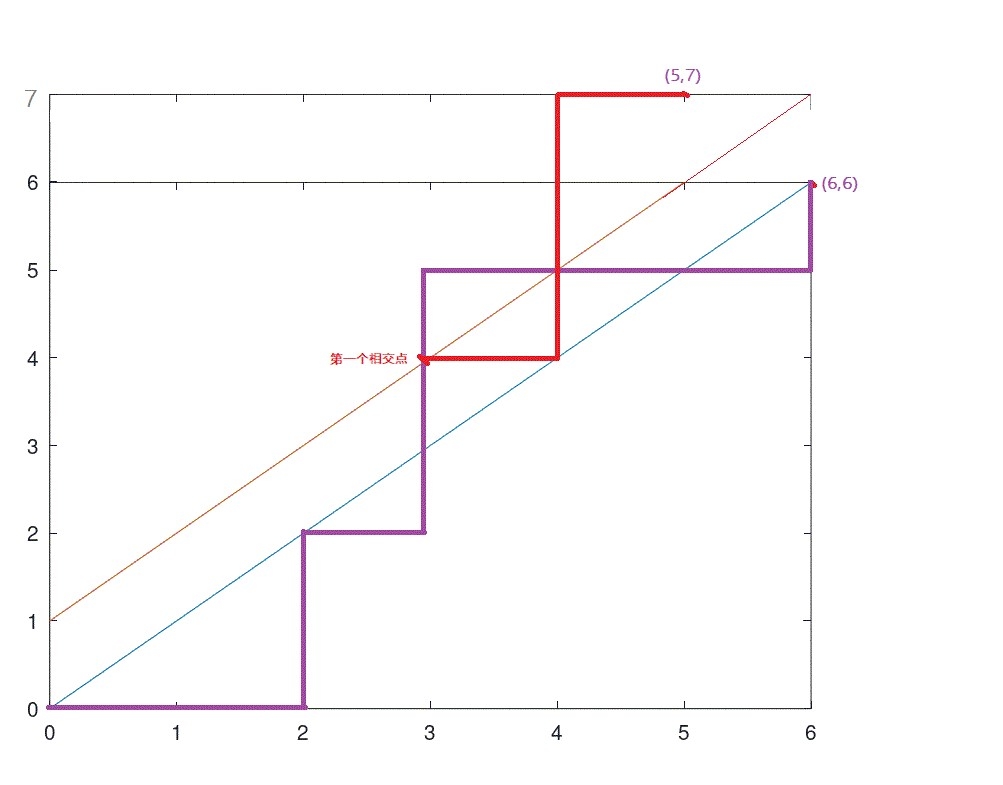
对于任何一条经过红颜色边的路径，找到第一个走到红边的点（第一个与红颜色边相交的点），将这条路径从这个点的后半部分关于红边做轴对称，（6，6）的对称点为（5，7）。

任何经过红颜色边的点都可以使用这种方式，找到第一个走到红颜色边的点，将后面的部分关于红颜色边做轴对称，则终点一定是（5，7）（即（6，6）关于红颜色边的对称点）。

任何一条从（0，0）到（6，6）经过红颜色边的点，通过上述方式都可以变成一条从（0，0）走到（5，7）的路径；而任意一条从（0，0）走到（5，7）的路径都会经过红颜色边，找到第一个经过红颜色边的点，关于红颜色边做轴对称，可以变成一条从（0，0）走到（6，6）并经过红颜色边的路径。从（0，0）走到（5，7）的路径与从（0，0）走到（6，6）且经过红颜色边的路径一一对应。

从（0，0）到（5，7）的所有路径为 $C_{12}^{5}$ ，则从（0，0）到（6，6）经过红颜色边的路径为 $C_{12}^{5}$ 。
从（0，0）到（6，6）不经过红边的所有路径个数： $C_{12}^{7}$ - $C_{12}^{5}$ 。

进行一般化，从（0，0）到（n，n）不经过红边的所有路径个数： $C_{2n}^{n}$ - $C_{2n}^{n-1}$

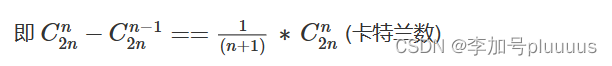
代码：

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int mod = 1e9 + 7;

int qmi(int a, int k, int p)
{
    int res = 1;
    while(k)
    {
        if (k & 1) res = (LL)res * a % p;
        k >>= 1;
        a = (LL)a * a % p;
    }
    return res;
}

int main()
{
    int n;
    cin >> n;
    int a = 2*n, b = n;
    int res = 1;

    // 卡特兰数计算公式
    for (int i=a; i>a-b; i--) res = (LL) res * i % mod;
    for (int i=1; i<=b; i++) res = (LL) res * qmi(i, mod-2, mod) % mod;
    res = (LL) res * qmi(n+1, mod-2, mod) % mod;

    cout<<res<<endl;

    return 0;
}

三、高斯消元

即求解线性多元方程组：

在这里插入图片描述

初等行列变化:

某一行乘上一个非零数,矩阵不变
某一行乘上一个常数加到另一行上,矩阵不变
交换矩阵中某两行的元素,矩阵不变

思路:

利用初等行列变化初等行列变化将矩阵变换成上三角形矩阵,再由后往前推出解。上三角形矩阵带来的结果有三种:无解,有唯一解,无穷多解。

无解:若在最后化成的上三角形矩阵中,正对角线中某个元素为0,但其所在行的最后一列元素不为0时,此时矩阵无解
有无数解:若在最后化成的上三角形矩阵中,存在正对角线中某个元素为0,且其所在行的最后一列元素也为0时,此时矩阵有无穷组解
有唯一解:若在最后化成的上三角形矩阵中,不存在正对角线中某个元素为0,此时矩阵有唯一解

算法步骤

枚举每一列c，找到当前列绝对值最大的一行
用初等行变换(2) 把绝对值最大的这一行换到最上面（注意：“最上面”指的是未确定阶梯型的行，而不是第一行）
用初等行变换(1) 将该行的第一个数变成 1 （其余所有的数字依次跟着变化）
用初等行变换(3) 将下面所有行的当前列的值变成 0

按照步骤从上到下变换成完美阶梯型：

再自下而上求每一行的解：

遍历完前 n 列后，如果当前没有走到最后一行的下一行，那说明简化之后的方程组的方程个数不足 n ，那么这时必然是无解或无数解。则从系数全是 0 的那行开始检查常数项，如果某个常数非 0 ，那就得到了0 = b i这个方程，是无解的；如果常数都是0 ，那是无数解；如果简化之后的方程组的方程个数恰好是n，那说明是唯一解，我们只需要将系数矩阵通过变换三变成单位阵即可。但是这个时候可以只变常数项，因为我们需要的只是变换后的常数项，这才是方程的解。

题目：

输入一个包含 n 个方程 n 个未知数的线性方程组。

方程组中的系数为实数。

求解这个方程组。

下图为一个包含 m 个方程 n 个未知数的线性方程组示例：

输入格式
第一行包含整数 n。

接下来 n 行，每行包含 n+1 个实数，表示一个方程的 n 个系数以及等号右侧的常数。

输出格式
如果给定线性方程组存在唯一解，则输出共 n 行，其中第 i 行输出第 i 个未知数的解，结果保留两位小数。

如果给定线性方程组存在无数解，则输出 Infinite group solutions。

如果给定线性方程组无解，则输出 No solution。

数据范围
1≤n≤100,
所有输入系数以及常数均保留两位小数，绝对值均不超过 100。

输入样例：
3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00

输出样例：
1.00
-2.00
3.00

代码：

对于行的元素改变操作，总是按列倒序遍历
#include<bits/stdc++.h>

using namespace std;
typedef double db;
const int N = 110;
/*  C++浮点数存在误差，不能直接判断0，要判断是否小于一个很小的数，
    如果小于这个很小的数，就认为是0，如小于1e-6*/
const db eps = 1e-8;

int n;
db a[N][N];

int gauss()// 高斯消元，答案存于a[i][n]中，0 <= i < n
{
        int c,r;
        for(c = 0,r = 0;c < n; ++c)//上界是小于n，因为是枚举系数矩阵的列
        {
                int t = r;
                // ① 找到当前这一列中绝对值最大的一行
                for(int i = r; i < n; ++i)
                {
                        if(fabs(a[i][c])>fabs(a[t][c])) t = i;
                }
                // 如果这一列中最大值已经是0了，直接continue进入下一列
                if(fabs(a[t][c])<eps) continue;//剪枝

                // ② 将这行换到最上面
                for(int i = c; i <= n; ++i) swap(a[t][i],a[r][i]);// 将绝对值最大的行换到最顶端
                
                // ③ 将该行第一个数变成1
                // 将r行中c列后的每一个元素除上一个a[r][c](该行的第一个不为零的元素)
                for(int i = n; i >= c; --i) a[r][i]/=a[r][c];// 将当前行的首位变成1

                for(int i = r+1; i < n; ++i)// 用当前行将下面所有的列消成0
                {
                        if(fabs(a[i][c])>eps)//剪枝
                        {
                                for(int j = n; j >= c; --j)
                                {
                                // a[r][j]当前这行的第j列元素,a[i][c]是下面行的最前面的元素
                                //目的是把第r+1行~n行的第c列元素都消除为0
                                        a[i][j] -= a[r][j] * a[i][c];//联想学线代怎么做的就行
                                }
                        }
                }

                ++r;
        }

        if(r<n)// 无解和无穷多解的判断
        {
            // 如果出现了等号左右一个为0一个非0，则说明无解
                for(int i = r; i < n; ++i)
                        if(fabs(a[i][n])>eps) return 2;// 无解
                // 否则说明有无穷多解
                return 1;// 有无穷多组解
        }
        
        // 回溯计算每个值xi
        for(int i = n-1; i >= 0; --i)
                for(int j = i+1; j < n; ++j)
                        a[i][n] -= a[i][j] * a[j][n];
//a[j][n]即代表之前循环已经求出来的未知数xj，a[i][j]代表当前枚举到的第i行中xj的系数，简单解个方程就行
        return 0;// 有唯一解
}

int main(){
        cin>>n;
        // 存储线性方程组的增广矩阵
        for(int i=0;i<n;++i)
                for(int j=0;j<n+1;++j)
                        cin>>a[i][j];
           

        int t = gauss();// 执行高斯消元

        if(t==2) cout<<"No solution"<<endl;// 否则无解
        else if(t==1) cout<<"Infinite group solutions"<<endl;// 如果 t = 1,线性方程组存在无数解
        else{
                for(int i=0;i<n;++i){
                        if(fabs(a[i][n])<eps) a[i][n] = 0;// 去掉输出 -0.00 的情况
                        printf("%.2lf\n",a[i][n]);// %.2lf 保留两位小数
                }
        }

        return 0;
}

四、简单博弈论

容斥原理：

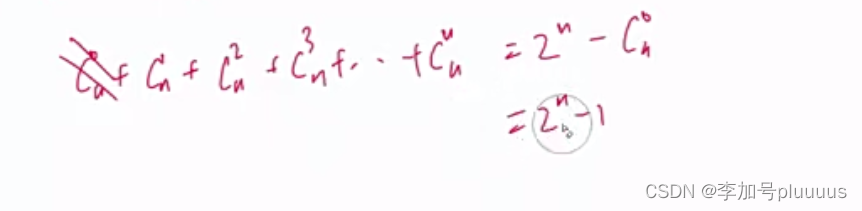
参考：

线性筛法求素数的原理与实现_太上绝情的博客-CSDN博客

约数和定理_百度百科 (baidu.com)

约数个数定理_百度百科 (baidu.com)

数论（三）——约数（约数个数，约数和，公约数）_c++约数求和_DearLife丶的博客-CSDN博客

常用代码模板4——数学知识 - AcWing

浅谈欧拉函数_liuzibujian的博客-CSDN博客

【ACWing】873. 欧拉函数_记录算法题解的博客-CSDN博客

欧几里得算法详解_辜月的博客-CSDN博客

Horner法则（秦九韶算法）的程序实现_秦九韶算法程序_远在远方的风比远方更远的博客-CSDN博客

快速幂算法（C++）_快速幂c++代码_L-M-Y的博客-CSDN博客

AcWing 875. 快速幂-数论-C++(递归、迭代、暴力) - AcWing

高斯消元（Gaussian elimination）_高斯消去法_努力的老周的博客-CSDN博客

AcWing 889. 满足条件的01序列 - AcWing

李加号pluuuus

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
算法基础课-第四章数学知识

同时，一个数既可能是pi的倍数也可能是pj的倍数，这样便重复减了，还需要加上（N / p1p2 + N / p1p3 +...+N / p1pk +N / p2p3 + ... + N / pk-1pk），然后根据容斥原理，后面还要加上三个数公共倍数的个数，减去四个数公共倍数的个数。而任意一条从（0，0）走到（5，7）的路径都会经过红颜色边，找到第一个经过红颜色边的点，关于红颜色边做轴对称，可以变成一条从（0，0）走到（6，6）并经过红颜色边的路径。互质的定义：互质是公约数只有1的两个整数，叫做互质整数。
复制链接

扫一扫