多智能体强化学习之值函数分解

最新推荐文章于 2025-03-19 12:38:26 发布

weixin_58246452

最新推荐文章于 2025-03-19 12:38:26 发布

阅读量2.6k

点赞数 5

文章标签：机器学习

本文链接：https://blog.csdn.net/weixin_58246452/article/details/131427115

版权

文章介绍了多智能体强化学习的三种主要范式：集中式学习、独立式学习和集中式训练分布式执行（CTDE）。集中式学习通过单智能体算法处理全局信息，但难以扩展；独立式学习忽略智能体间的交互；CTDE结合两者优点，但随着智能体数量增加，优化复杂度提高。值函数分解是解决这一问题的关键技术，通过DQN、VDN等方法来分解和学习多智能体系统的值函数。DQN和经验回放、目标网络的引入增强了学习的稳定性和效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

多智能体强化学习范式

多智能体学习有三种范式：集中式学习（Centralized Learning）、独立式学习（Independent Learning）和集中式训练分布式执行（Centralized Training with Decentralized Execution，CTDE）。

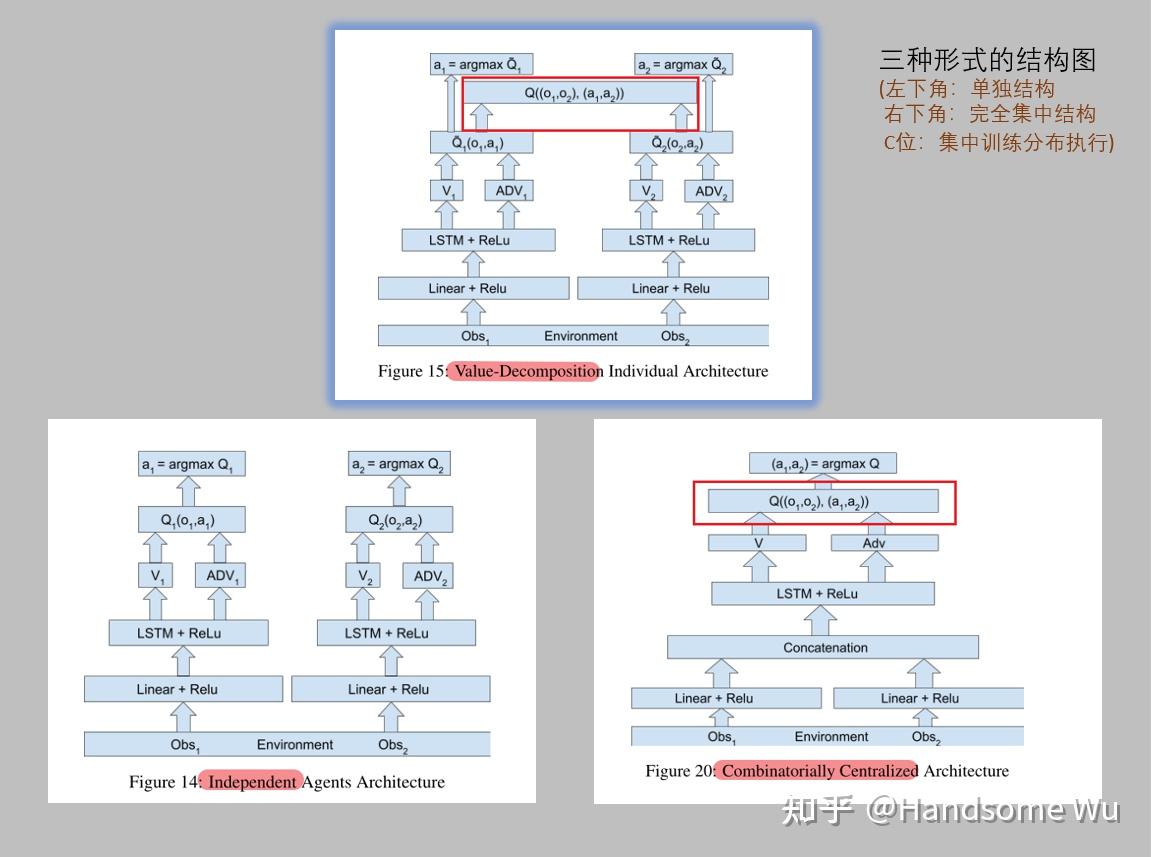
1、集中式学习将整个系统视为一个整体，采用单智能体强化学习算法训练，解决了环境非平稳问题，但需要上帝视角全局通信，不可扩展，无法解决无通信、大规模和大动作空间的问题。

MADDPG，是在深度确定策略梯度（Deep Deterministic Policy Gradient，DDPG）方法的基础上，对其中涉及到的 actor-critic 框架进行改进，使用集中式训练、分布式执行的机制。 MADDPG为每个智能体都建立了一个中心化的 critic，它能获取全局信息（包括全局状态和所有智能体的动作）并给出对应的值函数 $Q_{i}(s,a_{1},...,a_{n})$ ，这在一定程度上缓解了多智能体系统环境不稳定的问题。另一方面，每个智能体的actor只需要根据局部的观测信息做出决策，能够实现对多智能体的分布式控制。

2、独立式学习让每个智能体独立训练自己的策略，在一些合作任务中取得了不错表现，但是忽视了多智能体之间的联系，加剧了学习的不平稳性。

3、集中式训练，分布式执行作为折中，训练时拥有上帝视角，提高学习效率，执行时各自独立决策，一定程度上解决了多智能体学习问题，但随着智能体数量增加，最优联合值函数求解复杂。

值函数分解

在 MARL 的 policy-based 方法中，中心化的值函数是直接使用全局信息进行建模，没有考虑个体的特点。在多智能体系统是由大规模的个体组成时，这样的值函数是难以学习或者是训练得到收敛的，很难推导出理想的策略。并且，只依靠局部观测值，无法判断当前奖励是由于自身的行为还是环境中其它队友的行为而获得的。

值函数分解，其实就是找到一个合理的方法来精确地表示每个独立智能体的动作值 $Q_{i}$ 与中心网络中的 $Q_{tot}$ 之间的关系。因为多智能体强化学习模型训练参数是依赖于 $Q_{tot}$ 的，多智能体强化学习通过中心化网络接收全局状态信息 $s$ 并训练单个智能体的参数，其主要目的是解决的单个智能体不具备全局观察能力的缺点。

每一轮训练结束后，单个智能体独立执行自己的动作，但是不能准确表示 $Q_{i}$ 和 $Q_{tot}$ 之间的关系，训练出来的模型效果就很差，

值函数分解的目的就是在中心化网络中分解 $Q_{tot}$ 。

centralized training decentralized execution（CTDE）其实就是值分解，换句话说，中心训练分步执行。就是在训练阶段将所有的智能体的 $Q$ 以加性的方式组合在一起，在中心层训练，训练好的每个智能体各做各的。这样做有两个缺点：1）出现 “lazy agent” ；2）中心化训练会严重拖慢训练速度，因为每次训练都需要等所有的智能体都上传数据才行。

传统的DQN方法可以训练出一个联合智能体的动作价值函数 $Q_{tot}$ ，但遗憾的是，该函数并不能用于决策，因为部分观测问题使得每个智能体都无法获得 $Q_{tot}$ 的全部输入。一个可行的解决方案是用一定的方法将 $Q_{tot}$ 分解为 $Q_{i}$ 的函数，这样直接学习 $Q_{i}$ ，例如使用累计方法的VDN，设计单调函数的QMIX和使用先训练的 $Q_{tot}$ 再训练 $Q_{i}$ 的QTRAN方法等。

DQN

值函数估计方法引入

在值函数估计方法中，我们希望引入一个价值模型用来估计每个状态动作对的累计回报。其代价函数可以写为：

$L=\frac{1}{2}\sum_{a}^{}\sum_{s}^{}(Q(s,a)-Q(s,a;\theta ))^{2}$

其中 $Q(s,a)$ 为真实的累积回报的值函数， $Q(s,a;\theta)$ 为价值模型估计的累积回报，我们希望两者的差最小。采用梯度下降法可得参数的更新公式为：

$\theta_{t+1}=\theta_{t}+\alpha[Q(s_{t},a_{t})-Q(s_{t},a_{t};\theta)]\bigtriangledown Q(s_{t},a_{t})$

通常采用TD方法对真实的 $Q(s_{t},a_{t})$ 进行估计，最终更新公式为：

$\theta_{t+1}=\theta_{t}+\alpha[r(s_{t},a_{t})+Q(s_{t+1},a_{t+1};\theta_{t})-Q(s_{t},a_{t};\theta_{t})]\bigtriangledown Q(s_{t},a_{t})$

其中可以定义TD-error为：

$\delta_{t}=r(s_{t},a_{t})+Q(s_{t+1},a_{t+1};\theta_{t})-Q(s_{t},a_{t};\theta_{t})$

Q-Learning

贪心策略：智能体每次采取的动作受以下方程控制：

$\pi(s)=argmax_{a\in A}Q_{t}(s,a)$

其中 $Q_{t}(s,a)$ 是在时刻 $t$ ，智能体拥有的 $Q$ 表中 $(s,a)$ 对应的 $Q$ 值，由于每次选择动作都使得在现有经验下，后续的收益达到最大，所以称为贪心策略。

$\epsilon$ 贪心策略：智能体每次以 $\epsilon$ 的概率执行随机动作，以 $(1-\epsilon)$ 的概率执行贪心策略。这里的 $\epsilon$ 称为探索系数。

现在我们确定了智能体如何按照行为策略和环境进行交互采集数据，现在最重要的是，我们应该如何利用收集到的数据，更新我们的 $Q$ 表，让它最后能收敛到最优策略对应的 $Q$ 表。

Q-Learning 的增量式实现

增量式更新方法的一般形式是：

新估计值 ← 旧估计值 + 步长 × [ 目标 — 旧估计值 ]

表达式中的 [ 目标 — 旧估计值 ] 表示估计误差，误差会随着向目标的靠近而缩小。

在 Q-Learning 中，我们采用如下方程对Q值进行更新：

$Q(s,a)\leftarrow Q(s,a)+\alpha(R(s,a)+\gamma max_{a}Q(S^{'},a)-Q(s,a))$

Q-Learning 的l两个特点

异策略：行动策略和评估策略不是一个策略。行动策略采用了贪心的 $\epsilon$ -greedy 策略，而评估策略采用了 $maxQ(s,a)$ 贪心策略。

时间差分：从值函数更新公式可以看出时间差分，利用时间差分目标来更新当前状态动作值函数。TD 目标可以写成 $r_{t}+ \gamma max_{a}Q(s_{t+1},a)$

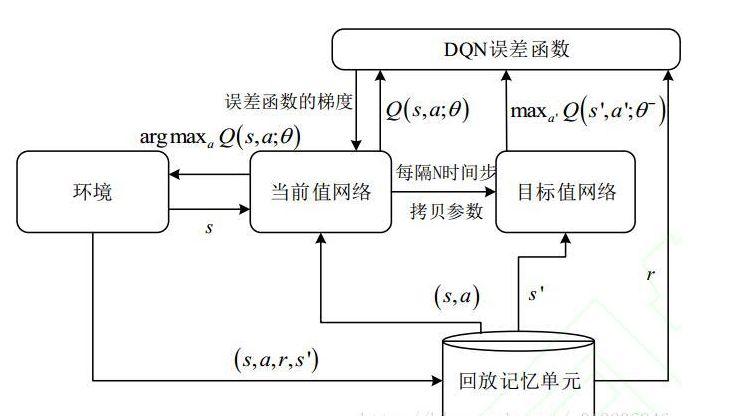
DQN

DQN 在 Q-Learning 的基础上作了如下修改：

1、DQN采用深度卷积神经网络逼近值函数；

2、DQN利用经验回放训练强化学习模型；

3、DQN独立设置了目标网络来单独处理时间差分算法中的 TD 误差。

输入

经过CNN卷积池化后得到 n 个state，而最终我们将会输出 K 个离散的动作。这 K 个离散的动作其实就是值函数，但此处的值函数 Q 不是一个具体的数值，而是一组向量，在神经网络中的权重为 θ，值函数表示为 $Q(s,a,\theta)$ ，最终神经网络收敛后的 θ 即为值函数。

近似和算法设置理论

整个过程的核心变为如何确定 θ 来近似值函数，最经典的做法就是采用梯度下降最小化损失函数来不断的调试网络权重 θ，Loss function 定义为：

$L_{i}(\theta_{i})=E_{(s,a,r,s^{i})\sim U(D)}[(r+\gamma max_{a^{'}}Q(s^{'},a^{i};\theta_{i}^{-})-Q(s,a;\theta_{i}))^{2}]$

其中， $\theta_{i}^{-}$ 是第 i 次迭代的目标网络参数， $\theta_{i}$ 是Q-Network 网络参数，接下来就是对 θ 求梯度：

$\frac{\partial L_{i}(\theta_{i})}{\partial \theta_{i}}=E_{(s,a,r,s^{i})\sim U(D)}[(r+\gamma max_{a^{'}}Q(s^{'},a^{i};\theta_{i}^{-})-Q(s,a;\theta_{i}))\bigtriangledown _{\theta_{i}}Q(s,a;\theta_{i})]$

在DQN算法出现之前，更新神经网络参数时，计算TD目标的动作值函数所使用的网络参数 θ 与梯度计算中要逼近的值函数使用的网络参数相同，这样就很容易导致数据间存在关联性，从而使得训练不稳定，为了解决关联性问题，TD目标计算时使用一个参数 $\theta^{-}$ ，计算并更新动作值函数逼近的网络使用另一个参数 $\theta$ ，在训练过程中，动作值函数逼近网络的参数 $\theta$ 每一步更新一次，TD 目标计算网络的参数 $\theta^{-}$ 每隔固定步数更新一次。

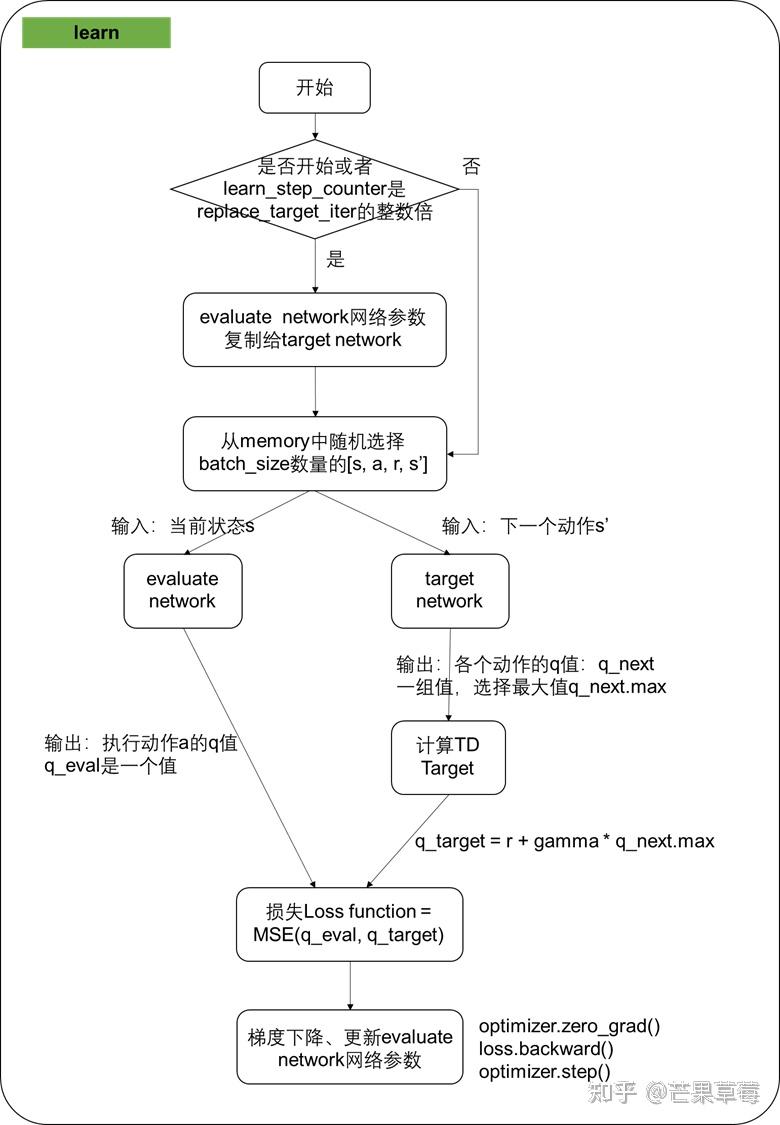
另外，在学习过程中，将训练的四元组存进一个 replay memory 中，在学习过程中以 min-batch 读取训练网络结构。

两个重要的思想：经验回放和目标网络。

经验回放：

将系统探索环境的到的数据储存起来，然后随机采样样本更新深度神经网络的参数。

原因：

1、深度神经网络作为有监督学习模型，要求数据满足独立同分布；

2、Q-Learning 算法得到的样本前后是有关系的。为了打破数据之间的关联性，经验回放方法通过存储-采样的方法将这个关联性打破了。

目标网络（和Q值网络结构完全相同）：

在一段时间内，目标 Q 值保持不变，一定程度上降低了当前 Q 值和目标 Q 值的相关性，提高了算法的稳定性。

结构框图

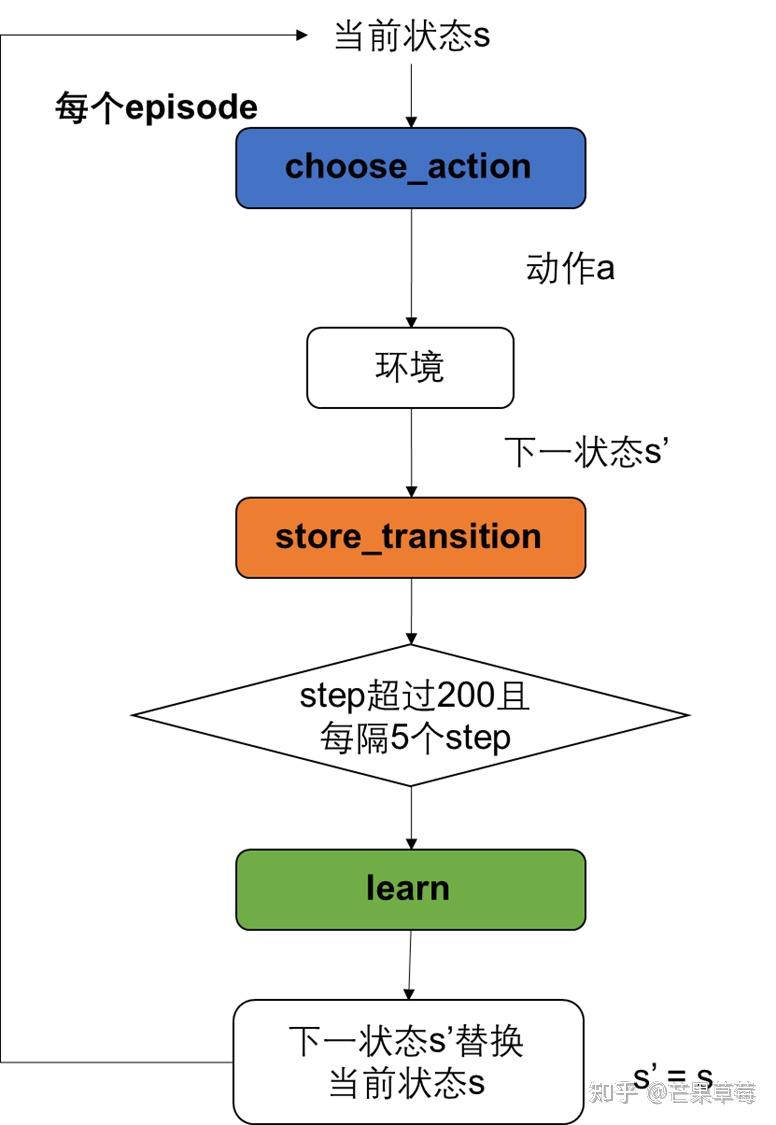
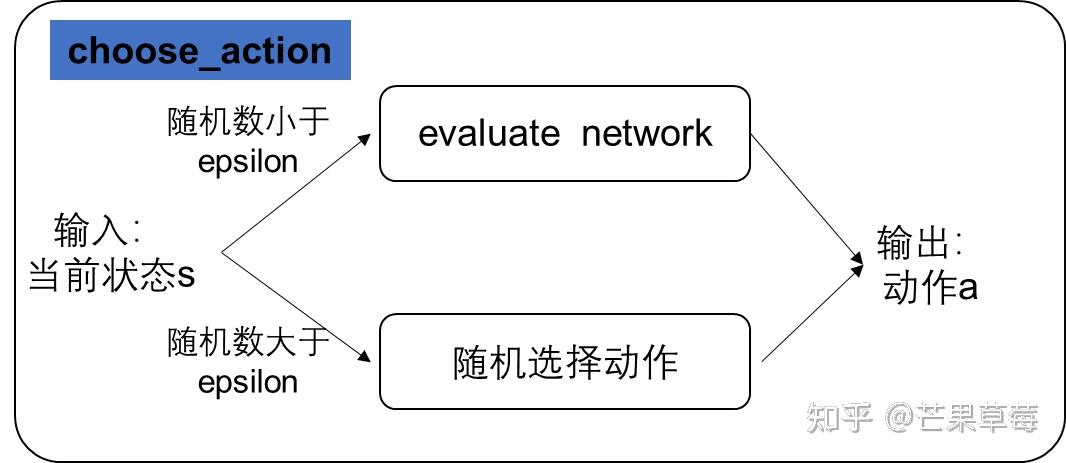
算法流程图

VDN

$Q_{tot}(s,u)=\sum_{i=1}^{N}Q_{i}(o_{i},u_{i})\approx \sum_{i=1}^{N}Q_{i}(h_{i},u_{i})$

在智能体1 的（o1，u1）不足以完全模拟 Q1 时，智能体1可能会在其LSTM中存储来自历史观测的额外信息，或者在通信通道中接收来自智能体 2 的信息。

近似得到Qtot之后，VDN使用DQN的更新方式，通过全局奖励 r 来更新 Qtot，其 Loss 函数表示为：

$L(\theta)=\frac{1}{M}\sum_{j=1}^{M}(y_{j}-Q_{tot}(s,u))^{2}$

其中，M 是 batch size， $y_{j}=r_{j}+\gamma arg max_{u}Q_{tot}^{-}(s^{'},u)$ ， $Q_{tot}^{-}=\sum_{i=1}^{N}Q_{i}^{-}(o_{i},u_{i})$ ， $Q_{i}^{-}$ 是target-net。

我们知道𝑄𝑖是经过神经网络得到的，它是一个 tensor，那么所有的𝑄𝑖加起来得到的𝑄𝑡𝑜𝑡𝑎𝑙也是一个 tensor，因此通过 TD-error 来更新𝑄𝑡𝑜𝑡𝑎𝑙，梯度会经过𝑸𝒕𝒐𝒕𝒂𝒍 反向传递给每个𝑸𝒊 (𝒐𝒊 ,𝒖𝒊 )从而去更新它们，这样就可以站在全局的角度去更新 𝑄𝑖 (𝑜𝑖 , 𝑢𝑖 )。