多智能体强化学习文献阅读记录（一）：Shapley Q-Value: A Local Reward Approach to Solve Global Reward Games

Shapley Q-Value: A Local Reward Approach to Solve Global Reward Games

Wang, J., Zhang, Y., Kim, T. K., & Gu, Y. (2020, April). Shapley Q-value: A local reward approach to solve global reward games. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 34, No. 05, pp. 7285-7292).

1. Problems

   • 全局奖励博弈

     ​ 全局奖励博弈是合作博弈的一个子类，所有智能体的共同目标是最大化全局奖励。

   • 奖励分配

     目前多采用共享全局奖励的方式，这可能会导致不正确的奖励函数，导致学习率下降。而局部奖励是指根据每个智能体的贡献来分配全局奖励。(VDN、QMIX、QTRAN等方法本质上也是进行奖励分配)

   ​ 在一般的合作式多智能体强化学习中，通常是找到一组NE作为稳定解，而NE通常更关注个人奖励，不能体现明确的合作激励。因此，共享全局奖励通常适用于智能体强制合作的情况。使用局部奖励可以反映每个智能体的贡献度。

2. Preliminaries

   • CG

     ​ 对于$G=<N,v>$,若对$\forall S,T\subset N,$满足：
     $$V(S)+V(T)⩽v(S\cup T)+V(S\cap T)$$
     则G称为凸博弈。

     ​ 设凸博弈G的一个解为$<CS,\vec{x}>$，其中 C S = { C 1 , C 2 , . . . , C m } CS=\{C_1,C_2,...,C_m\} CS={C1​,C2​,...,Cm​}表示一个联盟结构,用$C{S}_N$表示所有可能的联盟结构。$\vec{x}$表示分配给每个智能体的向量(本地奖励)，$\vec{x}$满足1.$x_i\ge 0,\forall i\in N$; 2.$x_i\ge v_i,\forall i\in N$。

     ​ 任意对策v的核心为：
     C ( v ) = { x ⃗ ∈ R n ∣ x ⃗ ( N ) = V ( N ) , x ⃗ ( S ) ⩾ V ( S ) , ∀ S ⊂ N } C(v)=\left\{ \vec{x}\in R^n\left| \vec{x}\left( N \right) =V\left( N \right) , \right. \vec{x}\left( S \right) \geqslant V\left( S \right) ,\forall S\subset N \right\} C(v)={x ∈Rn∣x (N)=V(N),x (S)⩾V(S),∀S⊂N}
     ​ 在核心下，没有一个子联盟有偏离目前的联盟结构而自己组建联盟的动机。

   • Shapley Value

     ​ Shapely值是合作博弈的一个特殊的单点解，其形式为：
     ϕ i ( v ) = ∑ S ⊂ N − { i } ∣ S ∣ ! ( ∣ N ∣ − ∣ S ∣ − 1 ) ∣ N ∣ ! ( v ( S ∪ i ) − v ( S ) ) \phi _i\left( v \right) =\sum_{S\subset N-\left\{ i \right\}}{\frac{\left| S \right|!\left( \left| N \right|-\left| S \right|-1 \right)}{\left| N \right|!}}\left( v\left( S\cup i \right) -v\left( S \right) \right) ϕi​(v)=S⊂N−{i}∑​∣N∣!∣S∣!(∣N∣−∣S∣−1)​(v(S∪i)−v(S))
     ​ Shapley值满足1.有效性：$x(N)=v(N)$、2.公平性：如果一个智能体没有贡献，分配的值就是0。如果要计算一个智能体的shapley值，必须考虑$2^{|N|}-1$个可能的联盟，因此本文中使用一种近似Shapley-Q值来代替。

   • Multi-agent Actor-Critic

     ​ 策略梯度方法通过直接最大化 $J(\theta )=$ ${\mathbb{E}}_{s\sim {\rho }^{\pi },a\sim {\pi }_{\theta }}[r(s,a)]$来学习策略$\pi$,由于$J(\theta )$的梯度不能直接计算，因此用以下方式来近似梯度计算：
     $${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{s\sim {\rho }^{\pi },a\sim {\pi }_{\theta }}\left[Q^{\pi }(s,a){\nabla }_{\theta }\log {\pi }_{\theta }(a\mid s)\right]$$
     ​ 在AC框架中， ${\pi }_{\theta }(a\mid s)$ 表示Actor， $Q^{\pi }(s,a)$ 表示Critic。 Actor负责执行动作，Critic负责为Actor执行的动作打分。

3. Solutions

   • ECG

     将原先的凸博弈拓展到无限视野和决策的场景，称为ECG

     ​ Stage1: 一个oracle安排联盟结构，签订合作协议。如果一个智能体加入其中某个联盟，则依据它的最佳长期贡献来分配给它奖励。假设oracle可以观测到整个环境，并且对所有智能体都很了解。

     ​ Stage2:每个智能体在加入被指定的联盟后，将根据策略函数${\pi }_i(a_i|s)$来最大化所在联盟的价值，从而实现每个联盟的最优价值以及个人奖励分配。(假设所有智能体都能观测到全局状态)

     ​ CS中的一个联盟C的最优价值为：
     $$ma{x}_{{\pi }_C}{v}^{{\pi }_C}(C)=E_{{\pi }_C}[\sum _{t=1}^{\infty }{\gamma }^{t-1}{r}_t(C)]$$
     其中,${\pi }_C={\times }_{i\in C}{\pi }_i$,$r_t(C)$表示由联盟C在时刻t获得的奖赏。根据凸博弈的性质，有：
     $$\begin{gathered} ma{x}_{{\pi }_{C\cup D}}{v}^{{\pi }_C}(C\cup D)\ge ma{x}_{{\pi }_C}{v}^{{\pi }_C}(C)+ma{x}_{{\pi }_D}{v}^{{\pi }_C}(D), \\ \forall C,D\subset N,C\cap D=\varnothing \end{gathered}$$

   引理1：1. 凸对策的核心非空 2.若$<CS,x>$是$<N,v>$的核心，并且分配方案x有效，则：$v(CS)\ge v(C{S}^{\prime }),\forall C{S}^{\prime }\in C{S}_N$
   

   定理1： 对于一个存在有效分配方案的ECG，在核心中一定存在一个关于大联盟的解，并且其目标是 m a x π v π ( { N } ) max_\pi v^\pi (\{N\}) maxπ​vπ({N})，即最大化团队总价值，即：
   m a x π v π ( { N } ) ≥ m a x π v π ( { C S ′ } ) , ∀ C S ′ ∈ C S N max_\pi v^\pi (\{N\}) \ge max_\pi v^\pi (\{CS'\}),\forall CS' \in CS_N maxπ​vπ({N})≥maxπ​vπ({CS′}),∀CS′∈CSN​

   定理1的proof
   

   ​ 从定理1可以看出，在适当的有效分配方案下，具有大联盟的ECG实际上等价于全局奖励博弈，其目标都是最大化全局奖励。这里假设所有智能体构成一个大联盟，因此ECG中的局部奖励方法在全局奖励博弈中是可行的。

   推论1：对于每个具有大联盟的ECG，shapley值一定是其核心。

• Shared Reward Approach

  ​ 共享奖励方法是指直接把全局奖励分配给每个智能体，每个智能体的目的都是最大化全局奖励，即：
  m a x π i v π ( { N } ) = m a x π i E π [ ∑ t = 1 ∞ r t ( N ) ] max_{\pi_i} v^\pi (\{N\}) = max_{\pi_i} E_\pi[\sum^\infty_{t=1}r_t(N)] maxπi​​vπ({N})=maxπi​​Eπ​[t=1∑∞​rt​(N)]
  ​ 其中，$r_t(N)$是全局奖励，$\pi$是所有智能体的联合策略。基于本文定义的ECG，可以将其改写为如下的等价优化问题：
  m a x π i v π ( { N } ) = m a x π i ∑ i ∈ N x i = m a x π i x i = m a x π i 1 ∣ N ∣ v π ( { N } ) max_{\pi_i} v^\pi (\{N\}) = max_{\pi_i}\sum_{i \in N}x_i=max _{\pi_i}x_i=max_{\pi_i}\frac{1}{\left| N \right|}v^\pi (\{N\}) maxπi​​vπ({N})=maxπi​​i∈N∑​xi​=maxπi​​xi​=maxπi​​∣N∣1​vπ({N})
  ​ 其中，$x$是针对大联盟N的有效分配方案。这说明共享全局奖励方法实际上是一个针对大联盟的有效分配方案。但这种方式不一定能找到最优解，因为 ( { N } , x ) (\{N\},x) ({N},x)不一定满足核心的条件。

• Shapley Q-value

  ​ 使用Shaley值来对每个智能体进行奖励分配，由于$v^{{\pi }_{C^{\prime }}}(C^{\prime })$表示联盟$C^{\prime }$在ECG中采取行动得到的奖励，因此可以用Q值来表示v。则定义每个智能体的Shapley Q-value定义为：
  Φ i ( C ) = Q π C ∪ { i } ( s , a C ∪ { i } ) − Q π C ( s , a C ) Q Φ i ( s , a i ) = ∑ C ⊆ N \ { i } ∣ C ∣ ! ( ∣ N ∣ − ∣ C ∣ − 1 ) ! ∣ N ∣ ! ⋅ Φ i ( C ) \begin{aligned} &\Phi_i(\mathcal{C})=Q^{\pi_{\mathcal{C} \cup\{i\}}}\left(s, \mathbf{a}_{\mathcal{C} \cup\{i\}}\right)-Q^{\pi_{\mathcal{C}}}\left(s, \mathbf{a}_C\right) \\ &Q^{\Phi_i}\left(s, a_i\right)=\sum_{\mathcal{C} \subseteq \mathcal{N} \backslash\{i\}} \frac{|\mathcal{C}| !(|\mathcal{N}|-|\mathcal{C}|-1) !}{|\mathcal{N}| !} \cdot \Phi_i(\mathcal{C}) \end{aligned} ​Φi​(C)=QπC∪{i}​(s,aC∪{i}​)−QπC​(s,aC​)QΦi​(s,ai​)=C⊆N\{i}∑​∣N∣!∣C∣!(∣N∣−∣C∣−1)!​⋅Φi​(C)​
  ​ 近似边际贡献:

  ​ 可以看出，在计算智能体对于其他联盟的边际贡献时，必须考虑$2^{|N|}-1$个可能的联盟。并且针对每一个联盟，都需要学习两个Q函数，然后计算两者之间的差异。这显然是复杂并且不稳定的，因此这里使用了一种方法直接计算近似的边际贡献：

  ​ 假设每个智能体按照顺序加入联盟，直到组成一个大联盟。有如下记号：
  P ⁡ ( C ∣ N \ { i } ) = ∣ C ∣ ! ( ∣ N ∣ − ∣ C ∣ − 1 ) ! / ∣ N ∣ ! \operatorname{P}(\mathcal{C} \mid \mathcal{N} \backslash\{i\})=|\mathcal{C}| !(|\mathcal{N}|-|\mathcal{C}|-1) ! /|\mathcal{N}| ! P(C∣N\{i})=∣C∣!(∣N∣−∣C∣−1)!/∣N∣!
  ​ P表示智能体i随机加入一个现有联盟C的概率，随后再与后来的智能体组成大联盟。据此定义如下的函数来直接近似边际贡献：
  Φ ^ i ( s , a C ∪ { i } ) : S × A C ∪ { i } ↦ R , \hat{\Phi}_i\left(s, \mathbf{a}_{\mathcal{C} \cup\{i\}}\right): \mathcal{S} \times \mathcal{A}_{\mathcal{C} \cup\{i\}} \mapsto \mathbb{R}, Φ^i​(s,aC∪{i}​):S×AC∪{i}​↦R,
  ​ 其中S是状态空间，C是智能体i希望加入的有序联盟， A C ∪ { i } = ( A j ) j ∈ C ∪ { i } \mathcal{A}_{\mathcal{C} \cup\{i\}}=\left(\mathcal{A}_j\right)_{j \in \mathcal{C} \cup\{i\}} AC∪{i}​=(Aj​)j∈C∪{i}​表示联盟 C ∪ { i } C \cup \{i\} C∪{i}中智能体的动作空间。

  ​ 在实际操作中，动作是有序的,用每个智能体动作向量的连接表示 a C ∪ { i } \mathbf{a}_{\mathcal{C} \cup\{i\}} aC∪{i}​，例如，C=(0,2)是一个有序联盟，则 a C ∪ { 1 } = ( a 0 , a 2 , a 1 ) \mathbf{a}_{\mathcal{C} \cup\{1\}}=\left(a_0, a_2, a_1\right) aC∪{1}​=(a0​,a2​,a1​)。为了保证在不同情况下映射 Φ ^ i ( s , a C ∪ { i } ) \hat{\Phi}_i\left(s, \mathbf{a}_{\mathcal{C} \cup\{i\}}\right) Φ^i​(s,aC∪{i}​)的输入一致，规定将所有智能体的动作进行连接，并用0来填充无关智能体。

  ​ 近似Shapley Q-value

  ​ 根据上述定义，可以将Shaply Q-Value记作：
  Q Φ i ( s , a i ) = E C ∼ Pr ⁡ ( C ∣ N \ { i } ) [ Φ i ( C ) ] Q^{\Phi_i}\left(s, a_i\right)=\mathbb{E}_{\mathcal{C} \sim \operatorname{Pr}(\mathcal{C} \mid \mathcal{N} \backslash\{i\})}\left[\Phi_i(\mathcal{C})\right] QΦi​(s,ai​)=EC∼Pr(C∣N\{i})​[Φi​(C)]
  ​ 为使上述SQ值便于计算，可以通过对概率分布P进行采样的方式来近似计算，即：
  Q Φ i ( s , a i ) ≈ 1 M ∑ k = 1 M Φ ^ i ( s , a C k ∪ { i } ) , ∀ C k ∼ Pr ⁡ ( C ∣ N \ { i } ) Q^{\Phi_i}\left(s, a_i\right) \approx \frac{1}{M} \sum_{k=1}^M \hat{\Phi}_i\left(s, \mathbf{a}_{\mathcal{C}_k \cup\{i\}}\right), \forall \mathcal{C}_k \sim \operatorname{Pr}(\mathcal{C} \mid \mathcal{N} \backslash\{i\}) QΦi​(s,ai​)≈M1​k=1∑M​Φ^i​(s,aCk​∪{i}​),∀Ck​∼Pr(C∣N\{i})

• SQDDPG

  ​ 在关于大联盟的ECG中，每个智能体只需要最大化自身的Shapley Vaule 即可使得全局奖励最大化，即：
  m a x π v π ( { N } ) = m a x π ∑ i ∈ N x i = ∑ i ∈ N m a x π i x i = ∑ i ∈ N m a x π i Q Φ i ( s , a i ) max_{\pi} v^\pi (\{N\}) = max_{\pi}\sum_{i \in N}x_i=\sum _{i \in N}max _{\pi_i}x_i=\sum _{i \in N}max _{\pi_i}Q^{\varPhi _i}(s,a_i) maxπ​vπ({N})=maxπ​i∈N∑​xi​=i∈N∑​maxπi​​xi​=i∈N∑​maxπi​​QΦi​(s,ai​)
  ​ 一个全局奖励博弈可以看作是一个势博弈，在势博弈中存在一个纯策略纳什均衡。因此，考虑使用DDPG方法(Deep deterministic policy gradient)去搜索最优的确定性策略。用Shapley Q-value代替DDPG中的Q函数，每个智能体的策略梯度为：
  $${\nabla }_{{\theta }_i}J\left({\theta }_i\right)={\mathbb{E}}_{s\sim {\rho }^{\mu }}\left[{{\nabla }_{{\theta }_i}{\mu }_{{\theta }_i}(s){\nabla }_{a_i}{Q}^{{\Phi }_i}\left(s,a_i\right)|}_{a_i={\mu }_{{\theta }_i}(s)}\right],$$
  ​ 其中 $Q^{{\Phi }_i}\left(s,a_i\right)$是智能体i的Shapley Q值，${\mu }_{{\theta }_i}$是其决定性策略。在每一个时间步，都可以获得一个全局奖励。由于每个智能体的Shapley Q-value都与本地奖励相关，因此不能直接根据全局奖励来更新每个智能体的${\hat{Q}}^{{\Phi }_i}\left(s,a_i\right)$。根据Shapley值的有效性，可以通过以下最小化问题来更新${\hat{Q}}^{{\Phi }_i}\left(s,a_i\right)$(相当于值函数分解)。
  $$\begin{array}{rl}\underset{{\omega }_1,{\omega }_2,\dots ,{\omega }_{\mid \mathcal{N}}\mid }{\min }& {\mathbb{E}}_{s^t,{\mathbf{a}}_{\mathcal{N}}^t,r^t(\mathcal{N}),s^{t+1}}[\frac{1}{2}(r^t(\mathcal{N})\\ & +{\gamma \sum _{i\in \mathcal{N}}{Q}^{{\Phi }_i}\left(s^{t+1},a_i^{t+1};{\omega }_i\right)|}_{a_i^{t+1}={\mu }_{{\theta }_i}\left(s^{t+1}\right)}\\ & {-\sum _{i\in \mathcal{N}}{Q}^{{\Phi }_i}\left(s^t,a_i^t;{\omega }_i\right))}^2]\end{array}$$
  ​ 其中,$\gamma (N)$是全局奖励，$Q^{{\Phi }_i}(s,a_i;w_i)$表示智能体i的Shapley Q值(被参数化为$w_i$),

4. Experiments

• Cooperative Navigation

  ​ 有三个智能体和三个目标点，没有为智能体分配指定的目标点，每个智能体要移动到其中一个目标。每个智能体在环境中的状态包括当前的位置，速度，与三个目标之间的距离以及与其他智能体之间的距离。每个智能体的动作空间向上、向下、向左、向右、留在原地。全局奖励是每个目标和离他最近的智能体之间的距离的和的相反数。如果发生了碰撞，则全局奖励将减少1。
  

• Prey-and-Predator

  ​ 在这个任务中，我们只能控制三个捕食者，猎物是随机的。每个捕食者的目的是通过协调，以尽可能少的步骤捕获猎物。每个捕食者的状态包括其当前的位置和速度，各自对猎物和其他捕食者的位移，以及猎物的速度。动作空间与协同导航中定义的空间相同。整体奖励是任何捕食者和猎物之间的负最小距离。如果猎物被任何捕食者抓住，全局奖励将增加10，游戏终止。
  

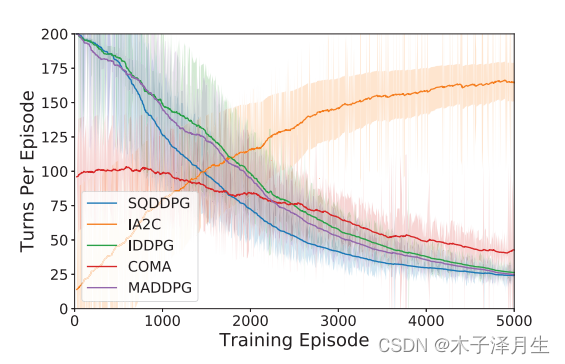
• Traffific Junction

  ​ 在此任务中，汽车沿着在一个或多个交通路口相交的预定义路线移动。在每个时间步，新的车以概率p出现到环境中，汽车总数限制在Nmax以下。在一辆汽车完成任务后，它将被从环境中移除，并可能被采样回一条新的路线。每辆车的视野有限，为1，这意味着它只能观察其周围3x3区域内的情况。在我们的实验中，与其他实验不同的是，汽车之间不允许进行通信（苏赫巴托、szlam和费格斯，2016年；Das等人，2018年）。每辆车的动作空间为燃气和制动，全局奖励函数为${\sum }_{i=1}^N-0.01t_i$。其中ti为车i在一次任务中在路上持续活动的时间步长，N为汽车总数。此外，如果发生碰撞，全球奖励将减少10。我们通过成功率（即没有发生碰撞的事件）来评估性能。

  

5. results

   ​ 在实验过程中，SQDDPG表现出了公平的信用分配和快速的收敛速度。