遗传算法C++实现求解VRP问题

 车辆路径问题（Vehicle Routing Problem, VRP）

1.问题描述

车辆路线问题（VRP）：一定数量的客户，各自有不同数量的货物需求，配送中心向客户提供货物，由一个车队负责分送货物，组织适当的行车路线，目 标是使得客户的需求得到满足，并能在一定的约束下，达到诸如路程最短、成本最小、耗费时间最少等目的。

2.VRP基因编码和解码方法 

假设1：仅有1个配送中心，在某一时刻，所有负责配送的车同时从 配送中心出发，分别完成各自的配送任务后，再回到配送中心（送奶路线）；

假设2：配送中心有若干辆车(如6辆)，一辆车可负责一个或多个点的配送任 务，且每个配送点只被服务一次。

假设3：每辆车有一定的载重量（如90t）和里程限制（如 200km），车的载重和行驶里程不可超过指定的值。

假设4：车辆必须在客户允许的时间窗处进行配送服务，此处采用硬时间窗

·编码

对于此问题，采用自然数编码，每个自然数代表一个客户，0代表配送中心，例如：

2

5

8

3

7

1

9

4

6

10

·解码

在解码过程中应该使每辆车在满足各种约束条件下为尽可能多的客 户提供服务。首先，安排第一辆车从配送中心0出发，到序列中的第一 个客户2处为其提供服务，服务完后再综合考虑车辆容量限制、行驶总路程限制以及序列中第二个客户5的时间窗限制等条件，决定是否直接到客户5处提供服务。 假若条件允许，则到客户5处，服务完再分析是否直接到客户8处提 供服务，依次类推；假若不能为客户8提供服务，则该辆车直接由客户5处返回配送中心，形成一个配送回路0->2->5->0。

接下来，安排第二辆车从配送中心0出发，直接到客户8处，服务完 再分析是否到后续客户3处为其服务。

依此类推，直到所有的客户都被服务为止，将客户序列拆分成了若 干个满足约束条件的配送回路，对应一个可行解。

注：为了使任何一个个体解码后都能对应可行解，本节假设从配送中心派一辆车单独为某一个客户提供服务，都可以在该客户的第一个时间窗内到达并完成服务。在实际中，假若从配送中心出发的车辆直接到 某个客户处服务，不能在该客户的第一个时间窗内完成服务，则说明该客户的第一个时间窗不可用，可以删掉该时间窗。因此，这种假设是有 意义的。

本程序可以调节是否可用交叉和变异，及其参数值，以及锦标赛法选取的后代数目可在参数设置区进行调节(默认0.1倍种群大小) ,仅仅将下面的两个数据文件与GA.cpp文件放在一个工程目录下即可运行代码。

3.实例：

设有一配送中心为10个客户提供货物配送服务，序号0表示配送中心， 序号1，2，…，10表示10个需求点。

配送中心共有6辆同型号的车辆，每辆车的最大装载量均为90t，每辆车的最长行驶距离均200km；

动用每辆车的固定成本均为50元，每辆车行驶每公里成本为20元；

配送中心及各个需求点之间的距离见表1；

车辆在配送中心及各个需求点之间的行驶时间见表2；

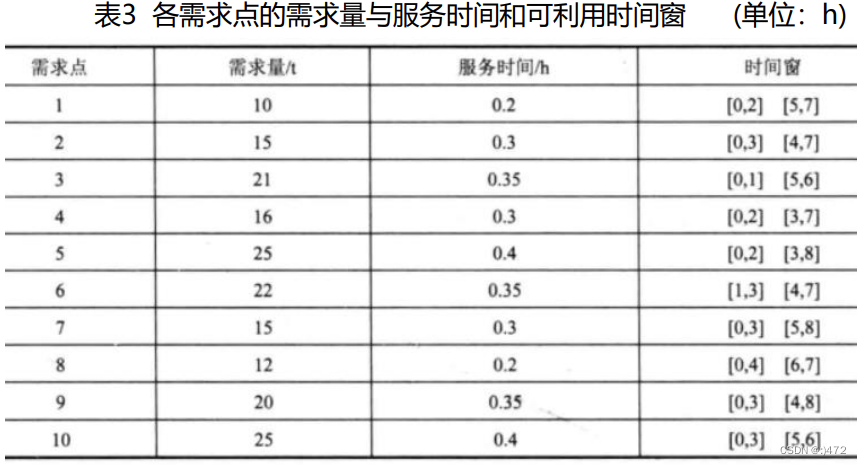
各个需求点的需求量、服务时间及可利用的时间窗见表3；

为了使总配送成本达到最少，需要安排多少辆车完成配送任务?每辆车的配送路径是什么?

 

 

 4.算法设计

（1）选择算子：随机遍历抽样（Stochastic universal sampling，SUS）

随机遍历抽样是轮盘选择的修改版本。使用相同的轮盘，比例相同，但使用多个选择点，只旋转一次转盘就可以同时选择所有个体。 这种选择方法可以防止个体被过分反复选择，从而避免了具有特别高适应度的个体垄断下一代。因此，它为较低适应度的个体提供了被选择的机会， 从而减少了原始轮盘选择方法的不公平性。

 （2）交叉算子：2点交叉（2-point crossover）+ 交叉映射+交叉概率

在2点交叉中， 交换两个父代个体中交叉点之间的基因序列，并形成交叉映射关系， 再按照交叉映射关系对其他位点的基因进行变换，得到两个新个体。

上面的两个父代对于选定的交叉点可以形成如下交叉映射关系：

4—5、8—7、2—10、11—3。

按照这样的映射关系，交叉后得到两个新个体

 

 （3）变异算子：交换突变（Swap mutation）+变异概率

（4）终止规则

采用一定的进化代数N作为终止规则，即当进化代数达到N时，终止计算，并把历代种群个出现的适应度最大的个体作为问题的最优解输出。

5.算法实现

（1）语言：C++

（2）环境：

操作系统：windows10家庭版

IDE：Visual Studio 2022

CPU：Intel Core i7-10875H 2.3GHz   实际速度：约4.3Ghz

内存：16GB DDR4 2933MHz

（3）源代码

//Time.h

#pragma once
#include<stdexcept>

// 时间窗类
class Time
{
public:
	// 默认构造函数
	Time() :start{ 0 }, end{ 24 } {}
	Time(unsigned start_, unsigned end_) :start{ start_ }, end{ end_ } {}
	//运算符重载
	bool operator<=>(const Time& other_time_window)const = delete;
	bool operator==(const Time& other_time_window)const = default;
	const auto& operator[](size_t index)const 
	{
		if (index == 0)return start;
		if (index == 1)return end;
		throw std::out_of_range{ " Time 对象下标越界!" };
	}
	unsigned start;		// 起始时刻
	unsigned end;		// 结束时刻
};

// Customer.h
#pragma once
#include<array>
#include<vector>
#include<compare>

#include"Time.h"

const size_t Window_num{ 2 };	// 时间窗个数
// 客户类，包括配送中心
class Customer
{
public:
	// 默认构造函数
	Customer();
	// 主构造函数
	Customer(unsigned number, unsigned requirement, double service_time, std::array<Time, Window_num> time_window);
	// 删除副本成员
	Customer(const Customer&) = delete;
	Customer& operator=(const Customer&) = delete;
	// 默认移动成员
	Customer(Customer&&)noexcept = default;
	Customer& operator=(Customer&&)noexcept = default;
	//运算符重载
	bool operator==(const Customer& other_customer) const { return m_number == other_customer.get_number(); }
	const auto& operator[](size_t index)const { return m_time_window.at(index); }
	auto& operator[](size_t index) { return const_cast<Time&>(std::as_const(*this)[index]); }
	// 类型转换
	operator size_t()const { return m_number; }


	// 访问器 //

	const unsigned get_number() const { return m_number; }
	const unsigned get_requirement() const { return m_requirement; }
	const double get_service_time() const { return m_service_time; }
	// 展示顾客属性
	void show_customer() const;
	// 获得与另一个顾客的距离
	unsigned get_distance(const size_t other_customer_number)const;
	unsigned get_distance(const Customer& other_customer)const;
	unsigned get_distance(const Customer* other_customer)const;
	// 判断是否在时间窗内
	double is_in_window(double time)const;

	// 访问器 //

	// 无更改器 //

	// 展示固有参数
	static void show_parameters();

	static const Customer Distribution_Center;							// 配送中心
	inline static std::vector<std::vector<int> > Distance_Matrix{};		// 客户以及配送中心之间的距离矩阵
	inline static std::vector<Customer> Customer_Array{};				// 客户序列，一般只在初始化时添加，不可修改
	inline static int Size{};											// 配送中心+客户数
	

private:
	unsigned m_number;											// 序号
	unsigned m_requirement;										// 需求量，单位t
	double m_service_time;										// 服务用时
	std::array<Time, Window_num> m_time_window{};				// 时间窗
};

// Car.h
#pragma once

#include"Customer.h"

// 车辆类
class Car
{
public:
	// 主构造函数
	explicit Car(unsigned number) :m_number{ number } {}
	// 默认副本成员
	Car(const Car&) = default;
	Car& operator=(const Car&) = default;
	// 默认移动成员
	Car(Car&&)noexcept = default;
	Car& operator=(Car&&)noexcept = default;
	//运算符重载
	const Customer* operator[](int index)const;
	Customer* operator[](int index) { return const_cast<Customer*>(std::as_const(*this)[index]); }
	// 类型转换
	operator size_t()const { return m_number; }

	// 访问器 //

	unsigned get_cost()const { return m_cost; }
	// 展示车辆属性
	void show_car()const;

	// 访问器 //


	// 更改器 //

	// 在路线后添加一个客户
	bool add_customer(const Customer* customer);
	//void add_customer(const Customer& customer);
	// 在时刻表后添加对应的时刻
	//void add_time(double time) { m_time.push_back(time); }
	// 计算配送成本
	void calculate_cost();
	// 更新时刻表
	bool update_time_list();

	// 更改器 //

	// 展示固有参数
	static void show_parameters(int choice = 0);
	
	inline static  unsigned Max_Amo