速算技巧（头同尾补与头补尾同）

目录

背景：

过程：

头同尾补：

步骤一：

步骤二：

步骤三：

步骤四：

步骤五：

头补尾同：

步骤一：

步骤二：

步骤三：

步骤四：

步骤五：

头尾互换两位数减两位数

步骤一：

步骤二：

步骤三：

11的乘法：

第一种情况：

步骤一：

步骤二：

步骤三：

步骤四：

第二种情况：

步骤一：

步骤二：

步骤四：

步骤五：

总结： 

---

背景：

速算技巧也被称为快速计算方法或速算法，速算技巧的学习应用不仅能够提高个人的计算速度和准确性，还有助于培养逻辑思维能力和数学兴趣，虽然速算技巧可以简化计算过程，但它们通常建立在坚实的数学基础上，因此在学习速算之前，理解和和掌握基本的数学概念和运算规则是非常重要的。

过程：

头同尾补：

适用于两位数乘法。具体来说，“头同尾补”指的是两个乘数的十位数字相同（即“头同”）并且个位数字相加正好等于十（即“尾补”）

速算口诀（（头+1）x头 尾x尾（占两位））

步骤一：

1.式子为61x69,被乘数为61，乘数为61，被乘数与乘数的十位数相同、个位数相加为10互补，因此符合我们的条件

步骤二：

2.根据口诀“头+1”，式子里头数为6，所以6+1

步骤三：

3.根据口诀中“（头+1）x头”，将上个步骤的计算结果和头数相乘，上个步骤的计算结果为7，头数为3，所以6x7

步骤四：

接着根据口诀“尾x尾（占两位）”，被乘数的尾数为1，乘数的尾数为9，所以我们用1x9

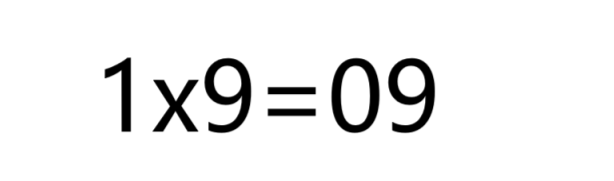
步骤五：

随后将第三步和第四步的计算结果一次写出来，得到计算结果

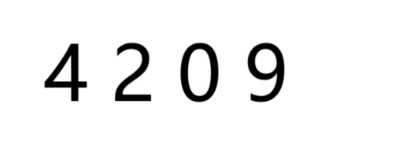
头补尾同：

两个乘数的十位数相加等于10（即“头补”），且个位数相同（及”尾同”）

速算口诀：（（头x头）+尾 尾x尾）

步骤一：

式子为28x88，被乘数为28，乘数为88，被乘数和乘数的十位相加为10互补、个位数相同，符合条件

步骤二：

按照口诀“头x头”，在例子中，被乘数头为2，乘数头8，使用2x8

步骤三：

在按照口诀“（头x头）+尾”，将上个步骤的计算结果与两数的尾数相加，在例子中，两数共同尾数为8，所以在加上8

步骤四：

继续按照口诀“尾x尾”，在式子中，被乘数与乘数共同的尾数为8，使用8x8

步骤五：

接下来，将步骤4和步骤5的计算结果依次写出来，得到结果

头尾互换两位数减两位数

适用于AB-BA（A和B分为代表十位和个位上的数字，且A不等于B）的算式

速算口诀：头剪尾，乘以九

步骤一：

1.算式为65-56，被减数为56，减数为65符合头尾互换的条件

步骤二：

2.根据口诀“头数-头数”，使用被减数的头数“6”减去减数的”5”

步骤三：

3.根据口诀“（头数-头数）x9”，我们使用第二步头数-头数的差和9相乘，得到结果

11的乘法：

两头一拉，中间相加”是11”的乘积速算的基本口诀。实际就死将被乘数的十位和个位数数字分别拉开，然后将它们相加，得到的和放在十位和个位之间，就构成了乘积

第一种情况：

个位数与十位数相加小于10：

步骤一：

1.两位数与11相乘（小于10），如图所示

步骤二：

2.首先将这个两位数（个位数与十位数相加小于10）写下来，然后将个位数与十位数中间空一位。

步骤三：

3.然后将个位数和十位数相加。

步骤四：

4.将个位数和十位数相加的和卸载之前的空一位上，所得到的数字就是结果

第二种情况：

个位数与十位数相加大于等于10：

步骤一：

1.两位数与11相乘（大于等于10）

步骤二：

2.还是将这两个数（个位数与十位数相加大于等于10）写下来，将个位数字与十位数字之前空一位

步骤三：

3.然后将个位数字和十位数字相加

步骤四：

4.将个位数数字和十位数字相加的和卸载之前的空格上

步骤五：

5.将所得的数字百位上加1，所得的数字就是要计算的结果

总结： 

总之速算技巧能够简化计算过程，减少计算时间，从而提高计算速度，等多种好处，最重要的是有助于培养和发展逻辑思维，底层逻辑认知觉醒。