图的着色问题与最大团问题的关系及改进

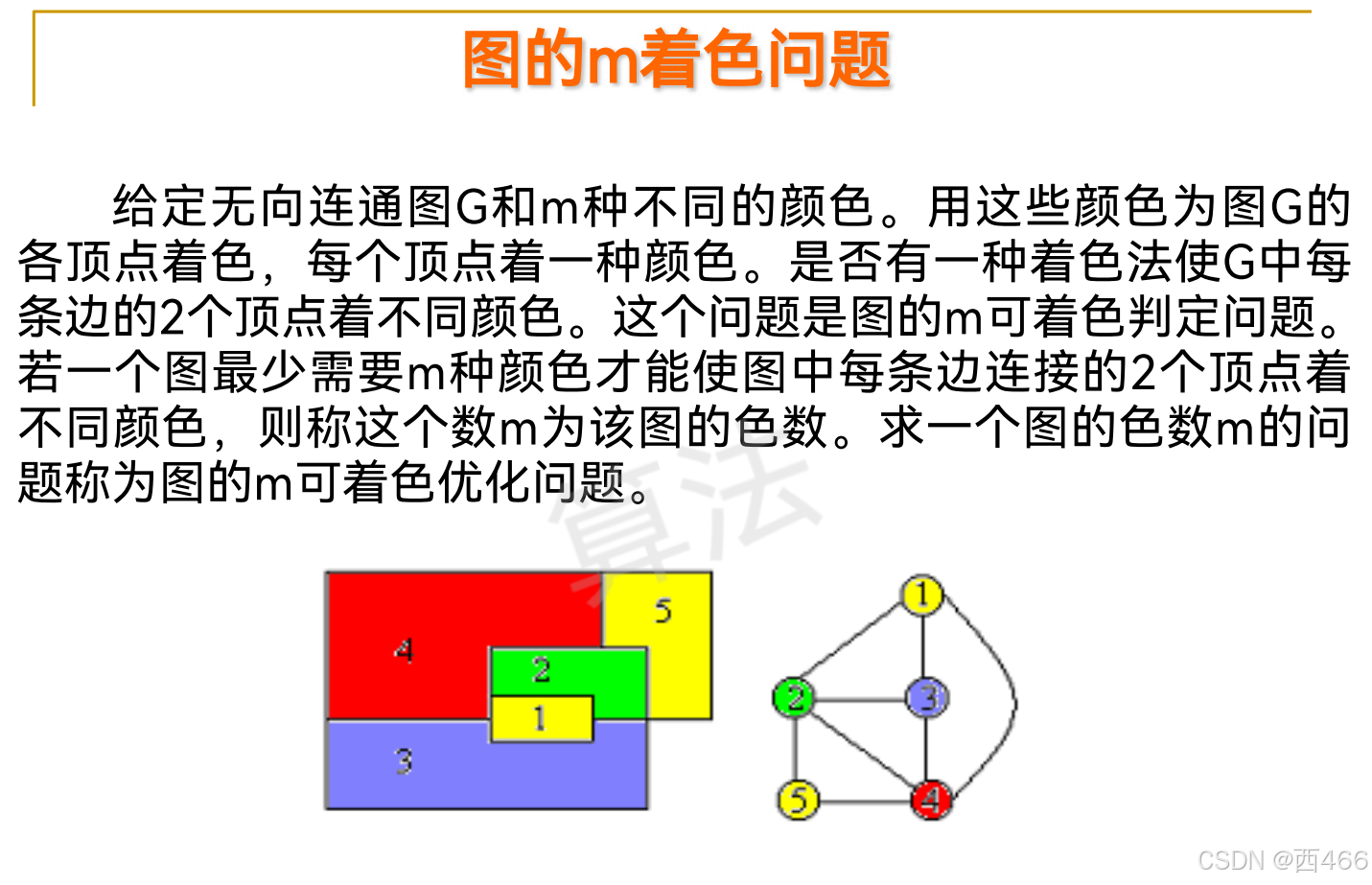
• 图的m着色问题

题目背景

算法分析

图的m着色问题是一个经典的图论问题，旨在判断一个图是否能用不超过m种颜色为其顶点着色，使得任意相邻顶点颜色不同。可采用如回溯法、贪心算法结合启发式策略、分支限界法，以及对于特定图类（如平面图）的线性时间算法等方法。

• ‌回溯法‌：通过递归尝试所有可能的颜色组合，当发现当前着色方案导致相邻顶点颜色冲突时回溯到上一步尝试其他颜色。此方法简单直观，但效率较低，尤其对于顶点数较多的图。
• ‌贪心算法与启发式‌：从某种“最优”的顶点开始着色，每次选择当前可用的最小颜色号，并尝试维持这种策略以减少后续冲突。启发式方法如DSATUR（最大度饱和策略）可显著提高效率。
• ‌分支限界法‌：结合回溯与剪枝技巧，通过评估当前着色方案的前景来提前终止无望的搜索路径，从而节省时间。
• ‌特定图类算法‌：对于平面图（任意顶点对间均不交叉的图），存在基于四色定理的线性时间算法，尽管四色定理的证明复杂，但实际应用中已有高效的实现方法。

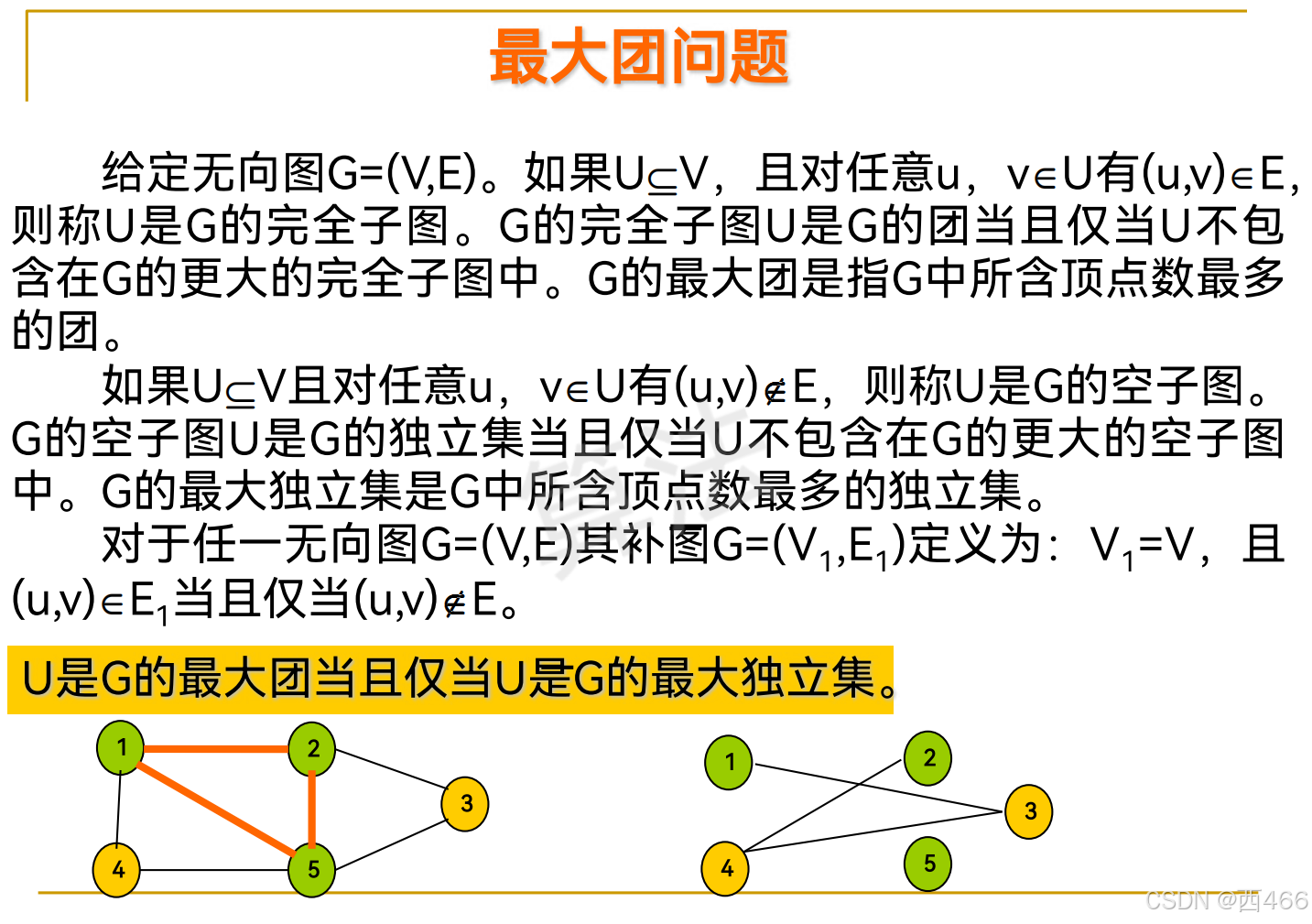
• 最大团问题

题目背景

算法分析

‌最大团问题是一种经典的组合优化问题，属于NP完全问题。‌最大团问题（Maximum Clique Problem, MCP）的目标是在给定的无向图中找到一个顶点数最多的完全子图，也称为团。

• ‌回溯法‌：回溯法通过递归地尝试所有可能的顶点组合，判断每个组合是否构成团。
• ‌分支限界法‌：这种方法通过扩展树或图来表示解空间，使用界限函数来剪枝，减少不必要的搜索。

• 二者关系

• 色数与团大小的关系：根据图论的基本定理，图的色数（最小着色数）X(G)和图的最大团大小W(G)满足关系X(G)≥W(G)。这意味着如果一个图可以用m种颜色着色，那么最大团的大小不会超过m。
• 启发式约束：通过m着色可以提供一个上界，从而减少最大团搜索的范围。

• 改进最大团问题上界

基于着色的启发式搜索：

步骤：

1. 先用贪心算法或其他快速方法对图进行着色，得到一个着色方案。
2. 设得到的着色数为m，这意味着最大团的大小w≤m。
3. 在枚举可能的最大团时，只考虑那些大小不超过m的子图，这样大大减少了搜索空间。

回溯与剪枝：

步骤：

1. 在回溯求解最大团问题时，维护当前找到的最大团大小k。
2. 每向前推进一层搜索树时，检查剩余顶点数与当前最大团的和是否有可能超过已知的最大团大小k。
3. 如果某一结点的扩展已经不可能超过当前的最大团大小k，则剪枝，不再继续搜索。

动态更新上界：

步骤：

1. 在算法执行过程中，动态更新图的着色数m。
2. 每当找到一个部分解（局部团），更新着色数m，并调整上界w≤m。
3. 这样可以不断收紧上界，加速算法在剪枝过程中的效率。