这就是卷积！

相位才是最重要的啊

于 2023-04-23 18:50:51 发布

阅读量321

点赞数 4

分类专栏：卷积文章标签：学习

本文链接：https://blog.csdn.net/weixin_59495044/article/details/130327350

版权

卷积专栏收录该内容

1 篇文章 0 订阅

订阅专栏

作者：小豪同学

知乎：相位才是最重要的

CSDN：相位才是最重要的啊

写在前面：

看这篇文章的人可能是初学卷积的人，也可能是想要对卷积有一定认识的人。不论你是前者还是后者，相信你都能够在本文中找到你想要的答案。

全文共计5400字左右，对于只是想要了解卷积是什么的人，只需要看完本文主题就好了，本文主体我举了本单词的例子来帮助大家理解卷积，之后又通过吃饭的例子加深大家对卷积应用的认识。对于讨厌数学和物理的读者来说也可以放心，因为本文主体并不涉及任何一个公式。看完之后，相信你能够对‘卷积是什么’这个问题有一个大致的答案。对于信号与系统的初学者来说，你还可以继续阅读本文（也就是本文的延伸阅读部分，需要读者有一定信号与系统的知识背景），延伸阅读部分我详细解释了信号与系统中的卷积，包括时域中输入与输出的关系，还有频率响应函数等，相信能够对你日后的学习有所帮助。

然而，不论是前半部分还是后半部分，本文都不会涉及到任何有关计算方法的部分，因为我觉得，相比于怎么算，“为什么计算卷积（或者说什么情况下要计算卷积）？”这个问题要重要的多，本文也是着重回答这个问题的。

你背单词的方法科学吗？

假设一个月之后你要进行六级考试，所以你希望在一个月内背尽可能多的单词（学过英语的深有体会吧）。假设我要在一个月背900个单词，那么，我该如何制定我的单词计划呢？

一天背30个！！！这样30天之后我就能背完900个单词啦。

可是这样就有个小问题，我今天背了30个，明天背30个，后天早上起来，我就会60个单词了吗？

显然不是，因为你会忘记的，那怎么办？

答案应该是：你需要知道遗忘单词的速度。

那如何获得遗忘单词的速度呢？

你可能已经想到了，就是它！

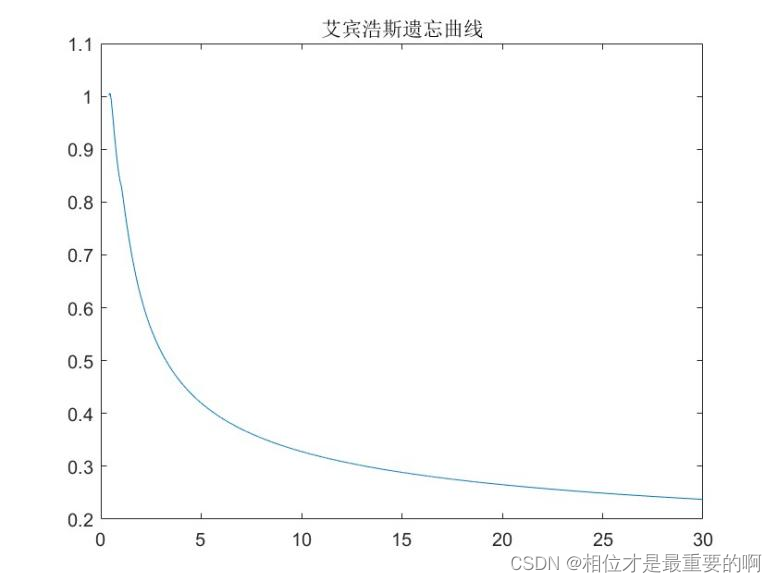现在我可以知道，我今天背了30个单词，明天还记得多少，后天还记得多少，30天后又记得多少。那如果我今天背30个，6天后又背30个，按照这个单词计划，30天我能背多少？

我们先将上面的艾宾浩斯遗忘曲线×30，得到下面的曲线：

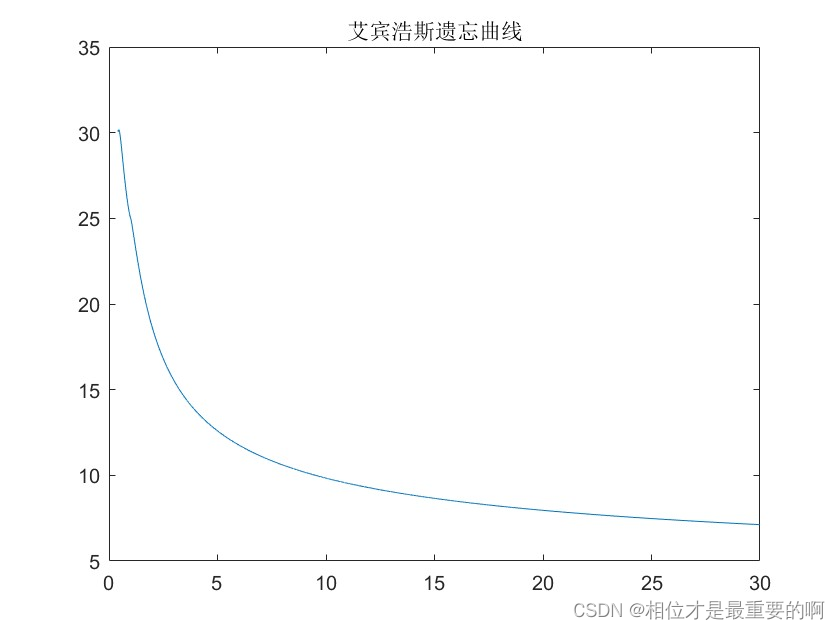之后实施我们的计划，只需要将上面的曲线以间隔为6向右平移，最后的情况应该是：

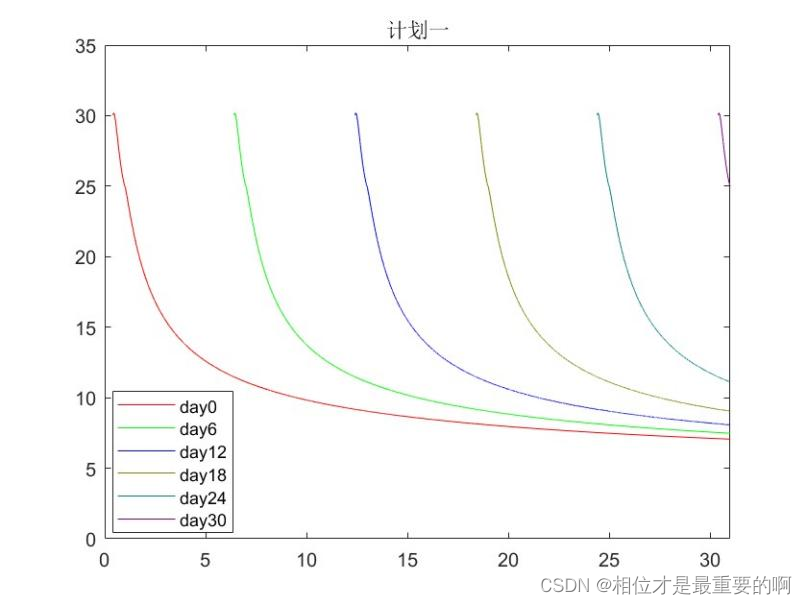实际上应该是离散的，所以应该是：

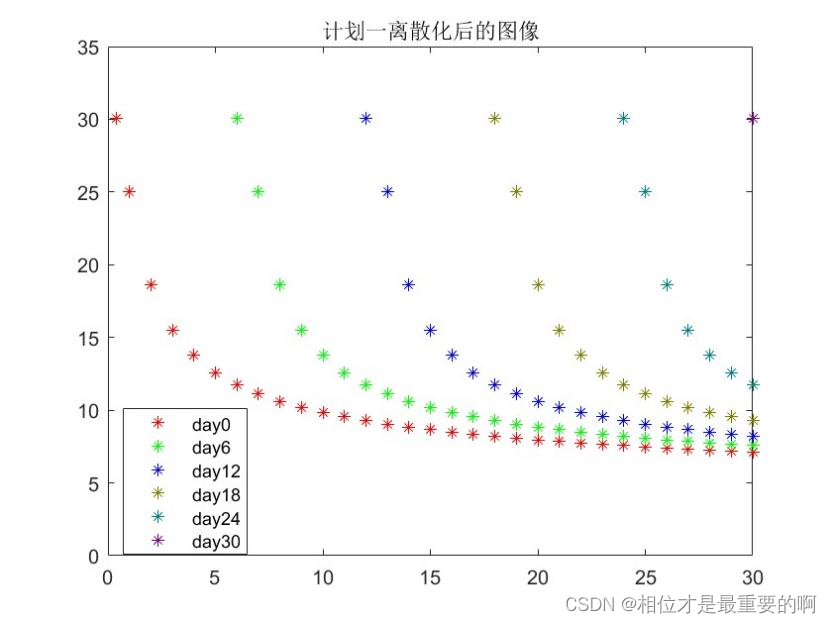然后，我们将今天背的，（今天还记得的）昨天背的单词，前天背的单词一直到第一天背的单词相加，就是到今天为止，我记住的总共单词，这个过程得到的结果可以用下面的这张图来表示：

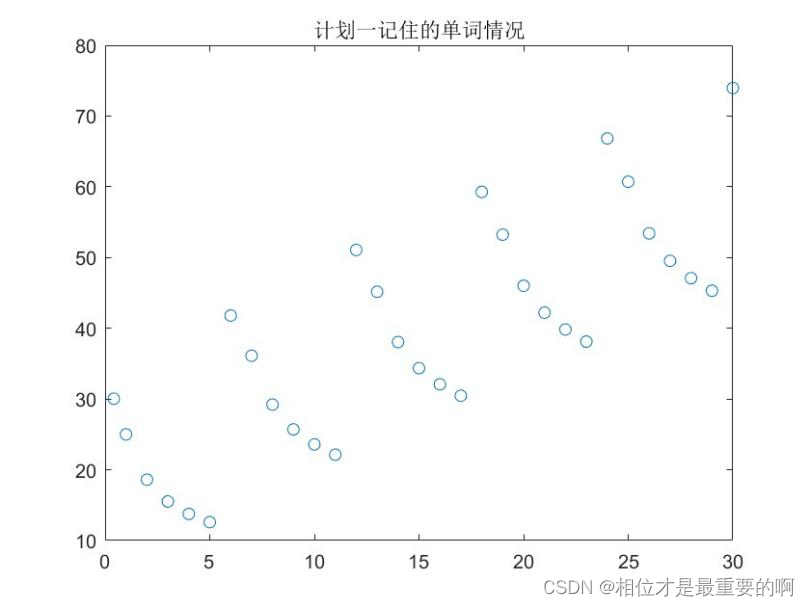如图所示，第30天记住的单词数大约只有74个，相比于不忘记的情况，足足少了（6*30-74=）106个。最后只记住了不到一半！

现在让我们再来考虑开头所讨论的计划（即每天背30个，背30天）。这个计划应该是这样的：

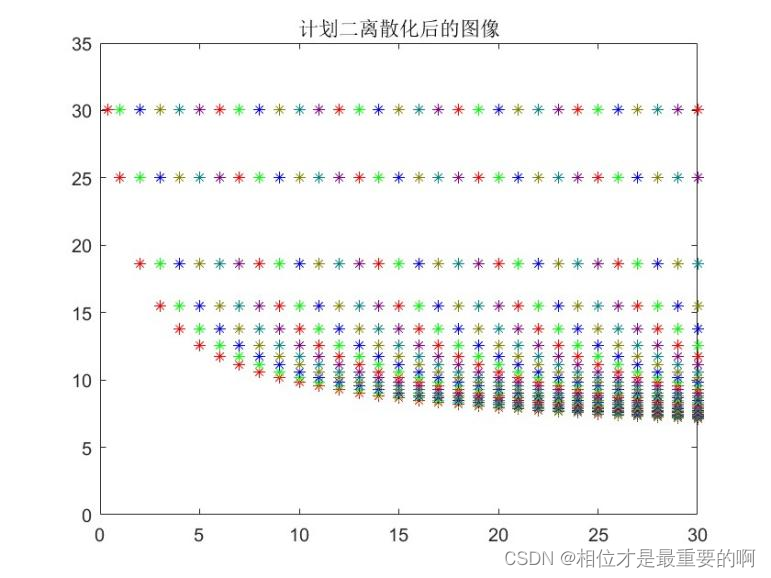最后得到的结果是：

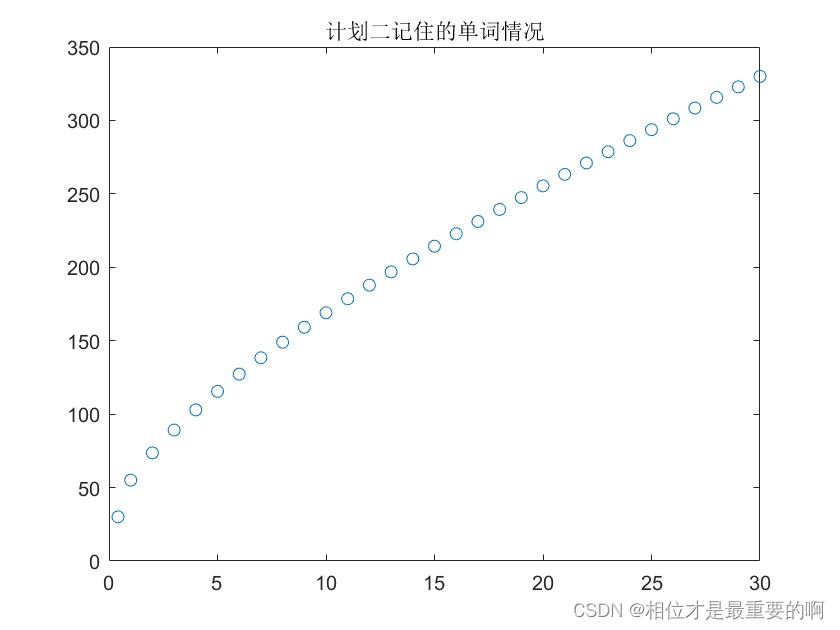在第30天，最后大脑中只记得330个。可见，想要在30天内背900个单词，每天背30个是行不通的。因此，如果你真的需要30天背900个单词，那么你就需要改变你的复习计划，比如，每天多背一些单词或者加入复习计划，让单词忘得不要那么快。

值得一提的是，我们最后得到的结果是一个函数，这意味着，我们不仅能知道30天之后能记住多少，我们还能知道第5天，第10天记住了多少（同理，我们还可以知道，如果这个计划一直持续下去，一年能记住多少单词），我们做了一件一劳永逸的事！

现在让我们再来回顾计划一，让我们看看我们都做了什么吧。

首先，我们认为，大脑不会记住我们背过的每一个单词，因此我们引入了艾宾浩斯遗忘曲线描述单词遗忘的速率。然后，我们制定了背单词的计划，也就是，6天背一次，每次背30个。我们将复习计划作用与艾宾浩斯遗忘曲线（也就是先将艾宾浩斯遗忘曲线×30，然后再平移，叠加），整个流程是这样的：

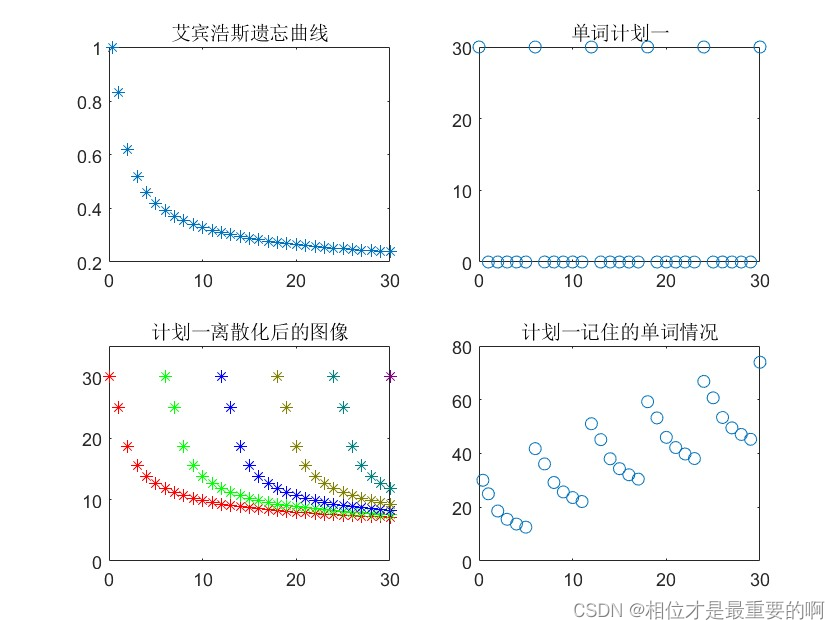这就是卷积（严谨来说是卷积和，因为我们考虑的是离散情况，不过它和连续情况的卷积是一个意思）！

从卷积角度再来解释一下我们刚才做的事情就是，我们找到了单词的遗忘速度--艾宾浩斯遗忘曲线，然后制定了单词计划，将两者的图像进行卷积，我们就得到了哪天能记住多少单词这个函数。

这简直太妙了，也就是说，现在我可以根据这个办法（卷积）来指导我的背单词计划（一定程度上），那么现在我就有了各种单词计划：

假如你有严重的拖延症，只有到快要考试的时候才想起来背单词，（假定单词计划为线性情况，也就是随着时间推移，每天背的单词越来越多）你的记忆情况应该是这样的（我就暂且将其命名为拖延版单词计划）：

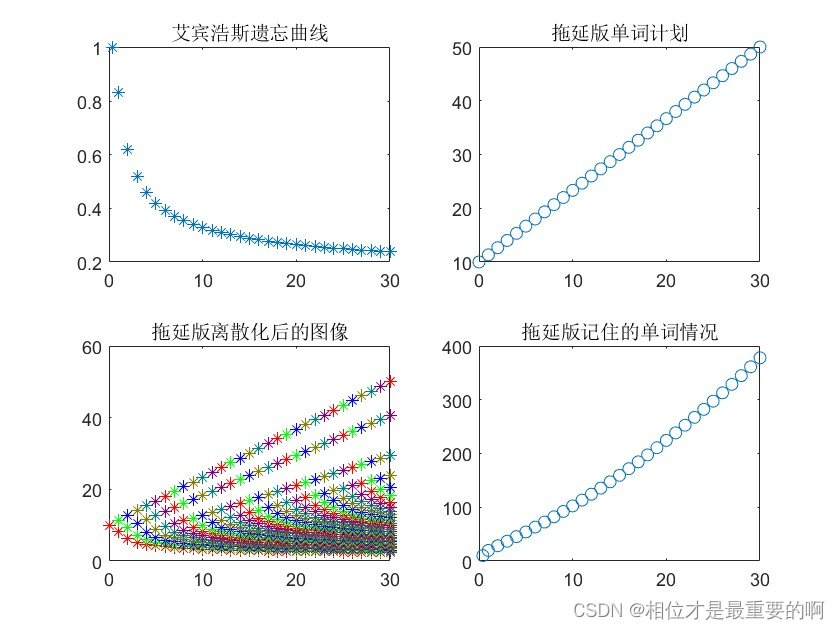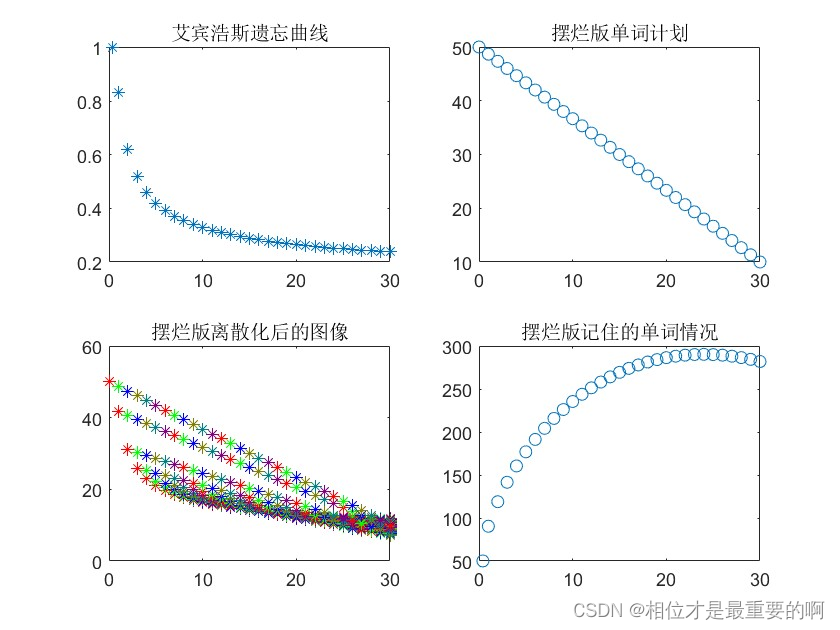
当然，还有摆烂版：

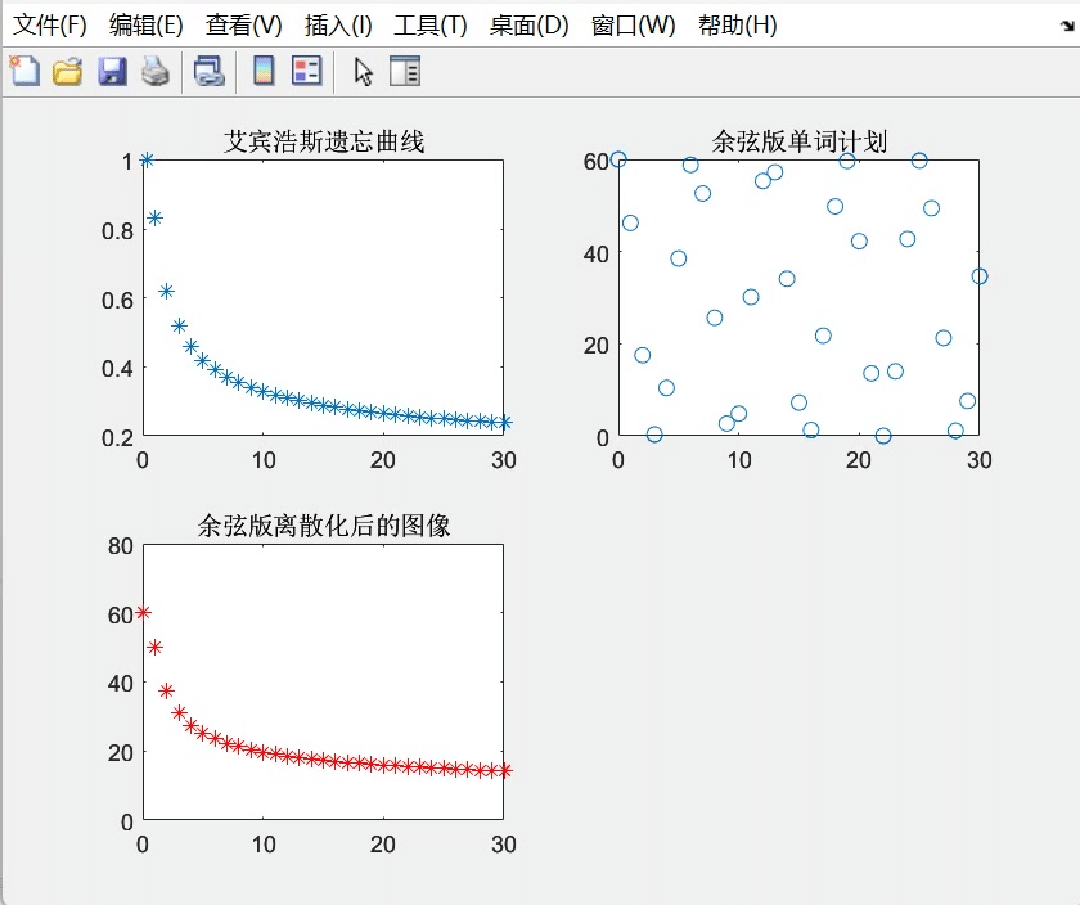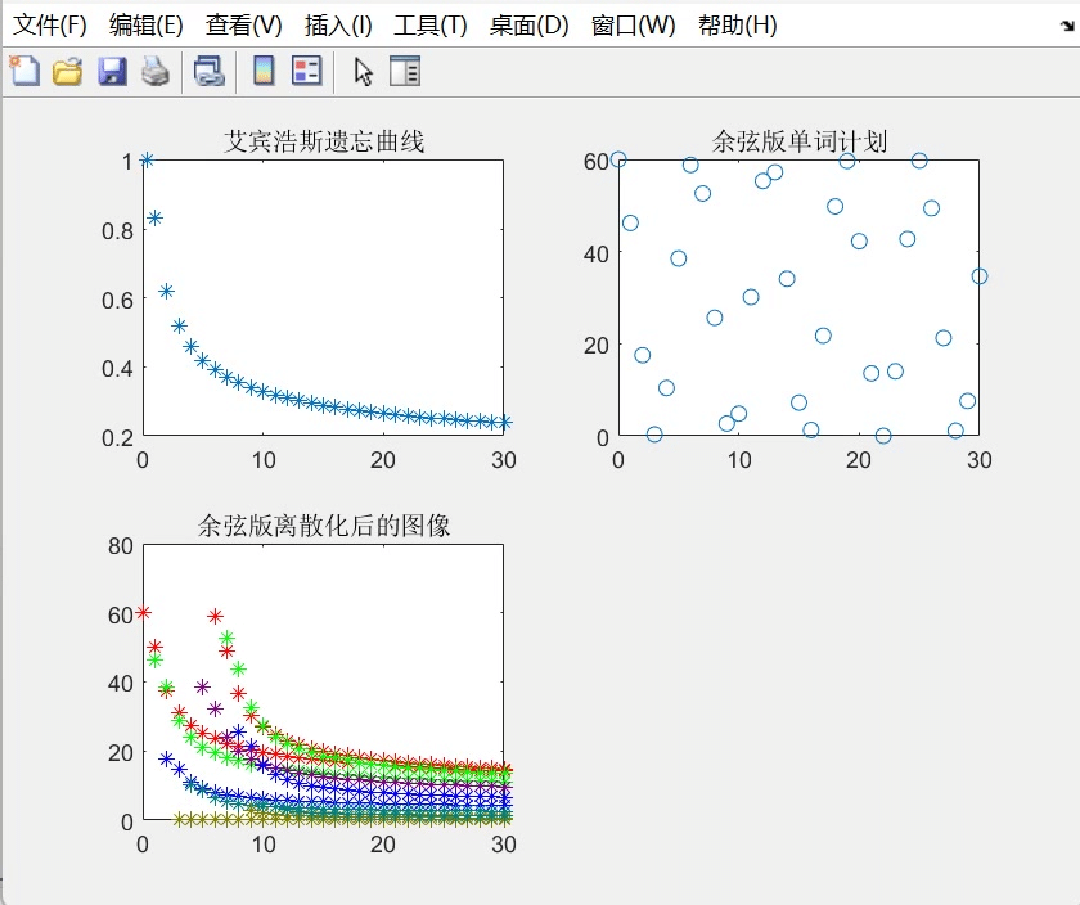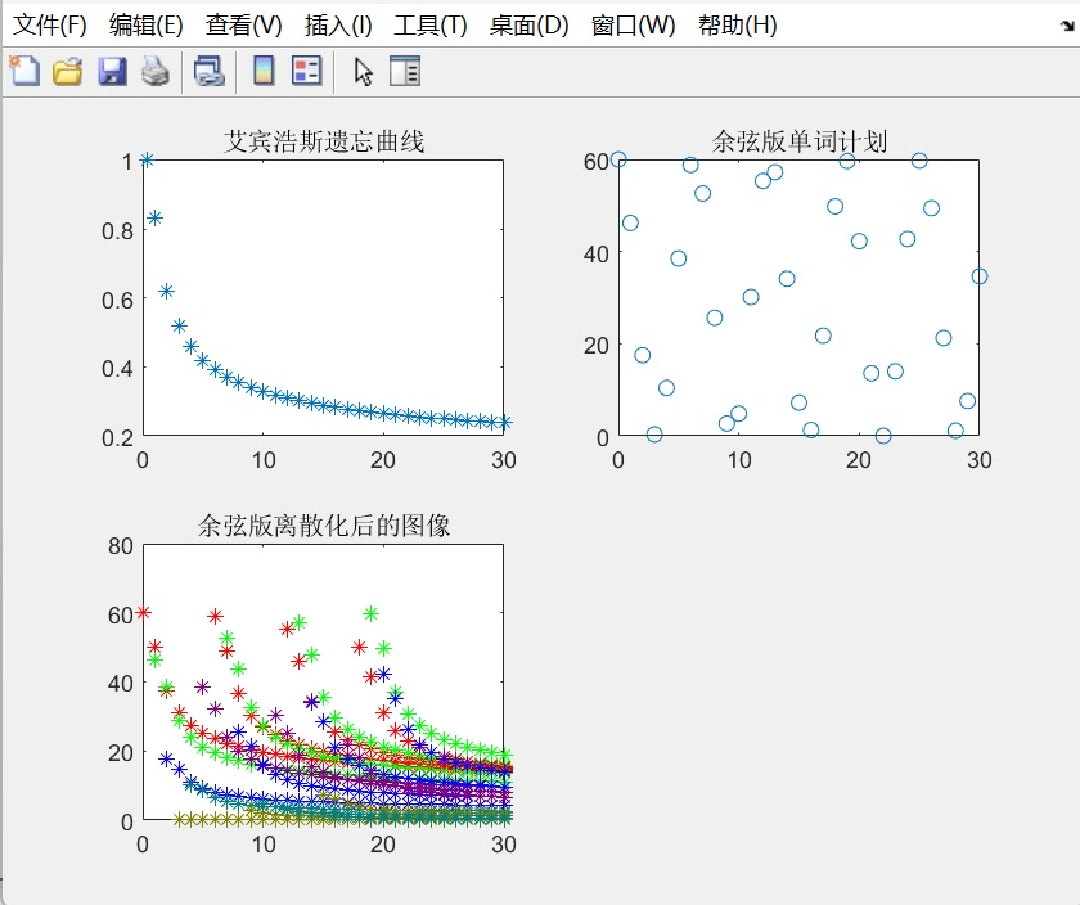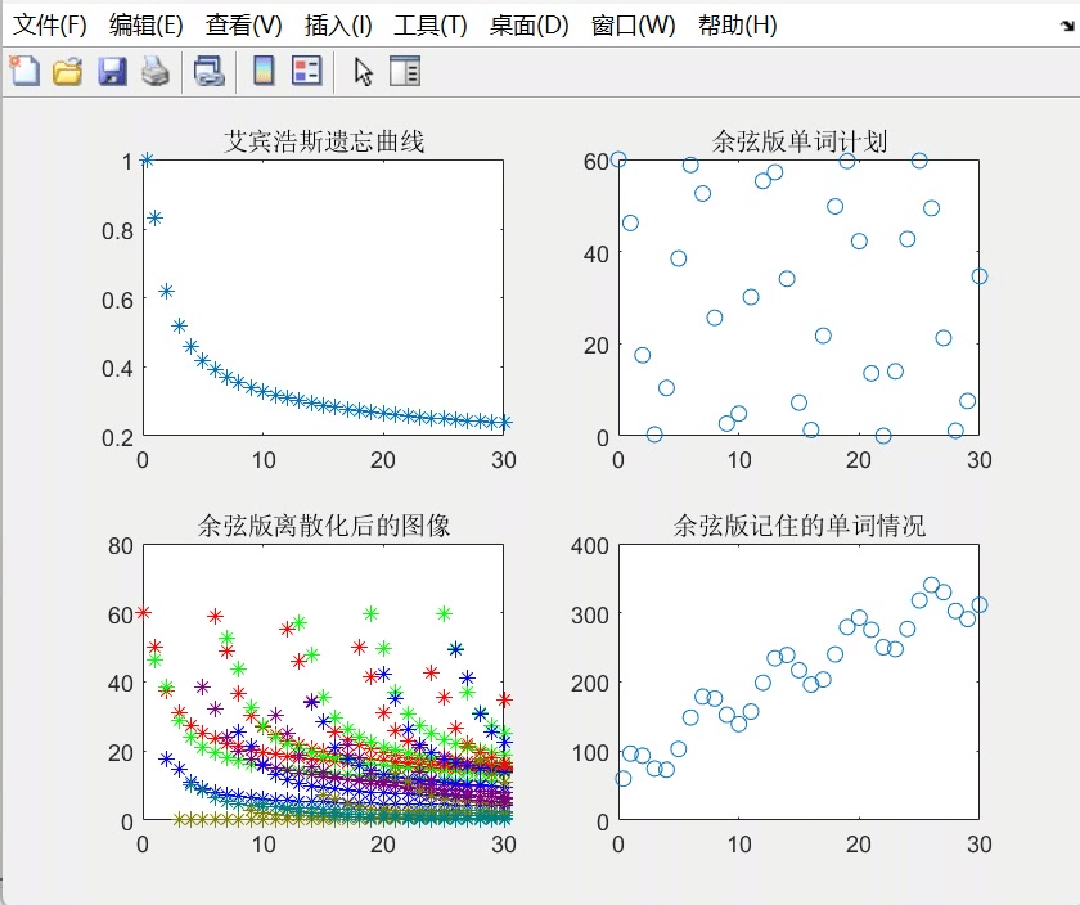
甚至如果你愿意的话，还有余弦版本的单词计划：

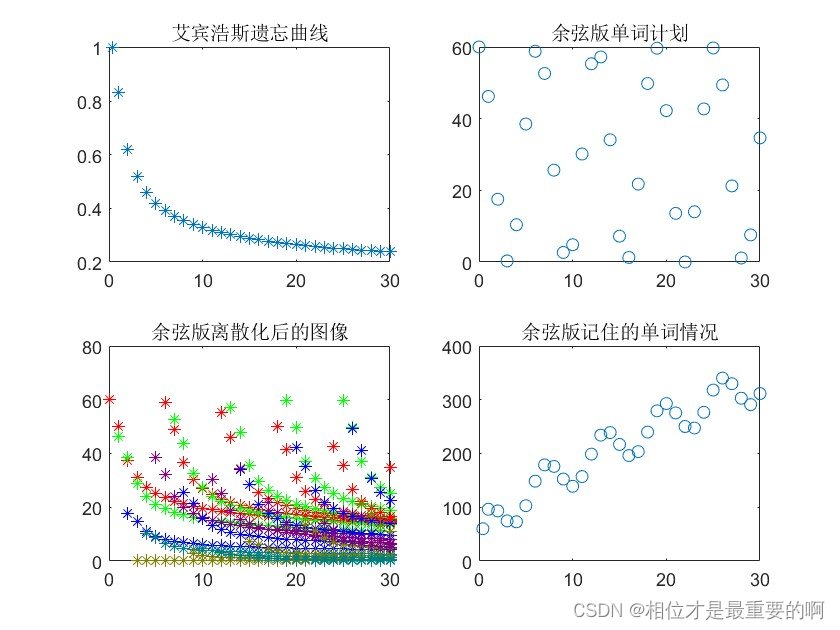图三（左下角得图）看起来貌似有点凌乱了，所以我在下面放一个gif（动图），也能够帮助大家更好理解这个过程：

现在，我就可以回答刚开始的那个问题了，也就是，为什么要进行卷积（或者说，什么情况下要进行卷积运算）？

根据我们之前考虑的情况，首先，最终我们想要的东西，某一天的输出不仅与当天的输入相关，还和之前的输入相关（今天的记住的单词=今天刚背的+昨天背的记住的+前天背的记住的+……）。然后，他要是一个线性时不变系统（今天的记住的单词=今天刚背的+昨天背的记住的+前天背的记住的+……，他们之前的关系是相加而不是平方什么的。而且现在背完的单词即刻生效，而不是等到10天20天之后）。

好了这就是卷积的应用情况，我之前还看到这样一句话，我觉得很有道理：为什么要进行卷积？因为卷积更能够反映现实世界之中的生活。

是的，因为，你前一秒钟所作的事情的状态不会立刻消失，它会损耗一点，然后叠加到下一个状态之中（系统中有类似于“储能”和“缓冲”作用的物体，在上面的单词计划中，我们的大脑就起到这样的作用）。如此往复，得到了最后的输出，也就是事情的结果。

卷积可以应用于任何类似于这样的场景。比如，吃饭。

我们先来分析一下这个过程，当我感觉到饿的时候，我就会吃饭。我刚吃的饭可以持续一段时间，让我不会感到饥饿（吃饭就是提供能量，人活动就是在消耗能量），一旦能量的消耗低于某个阈值，我就会感觉到饥饿，因此需要再次吃饭补充能量。也就是下面这张图所示：

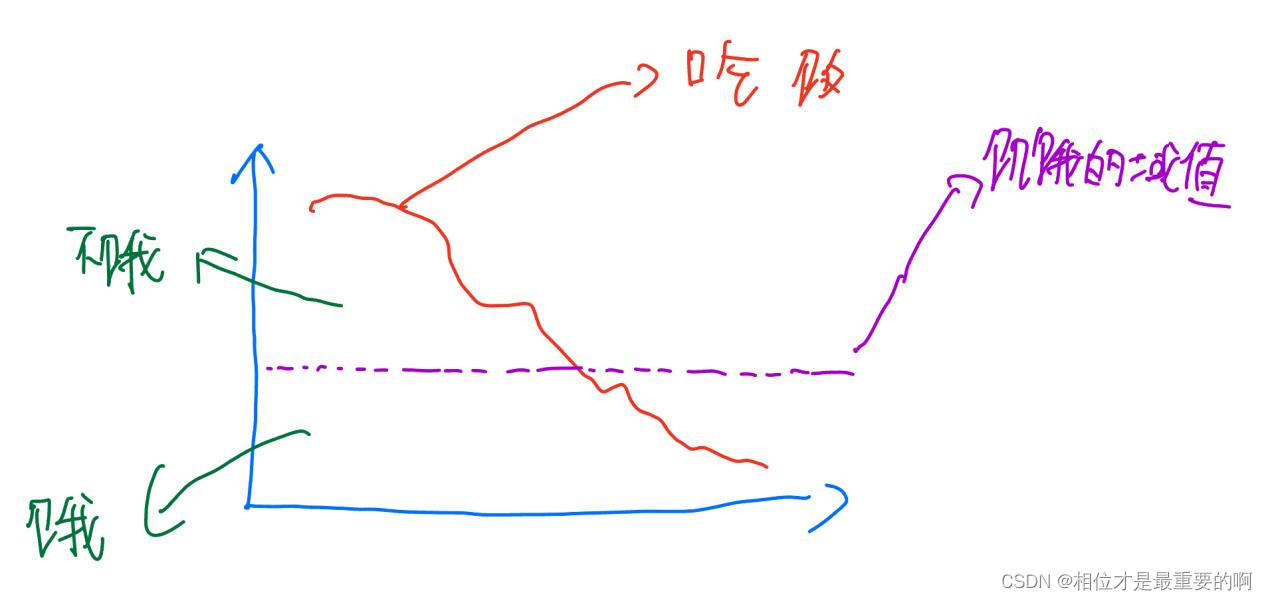这样我们就找到了消耗能量的曲线（相当于上文中的艾宾浩斯遗忘曲线），然后再制定吃饭时间，还有吃多少就好了（也就是上文中的单词计划）。然后再将两曲线卷积（平移，叠加）。我就能明白，我在什么时候会感觉到饥饿了。

然而，这件事情可能并没有那么简单，我们似乎忽略了一些事情。第一，人体各时间消耗能量的速度真的一样吗（也就是说，白天和夜晚消耗能量的速度是一样的吗）？第二，我计算出来的结果真的具有普适性吗（也就是说，我可以根据此图像来预测明天什么时候饥饿？可是，每天吃的都一样？每天吃饭的时间都一样？）？第三，每天能量消耗的速率都是一样的吗（如果今天下午有体育课，那那个时刻的消耗速率会不会快一些？）……

因为有上面所说的各种各样的问题，这个模型实际上并不适用于人。即使能够适用，我们也没有办法保证每天干的事情都一样，吃饭时间都一样，吃的东西都一样。如果强行要用，结果就是，可能每天都需要重新计算。可能你算了半天还不如说一句，我饿了。毕竟，相比之下，你自己的感受才是最重要的。

那么，分析了这么半天，都是无用功喽？

不是的，只是因为人的活动太复杂，太具有个性化，所以才不可预测，更重要的是，人会说话表达自己的感受。因此，它适用于另外一部分生物--宠物或者是牲畜。

毕竟，跟人相比，它们每天的生活可单调多了，而且，它们也不会张口说，我饿了（可能也会，只是我们听不懂），更不会自己拿钱去买饭，它们只能等我们去给它们喂饭。

这样就简单多了，我们假定他们消耗能量的速度是线性的（因为活动很单调），然后在制定喂粮计划，将二者进行卷积，就可以得到小狗身体的能量曲线，知道他们什么时候会饿。

那么，整个过程可以用下面这张图来表示：

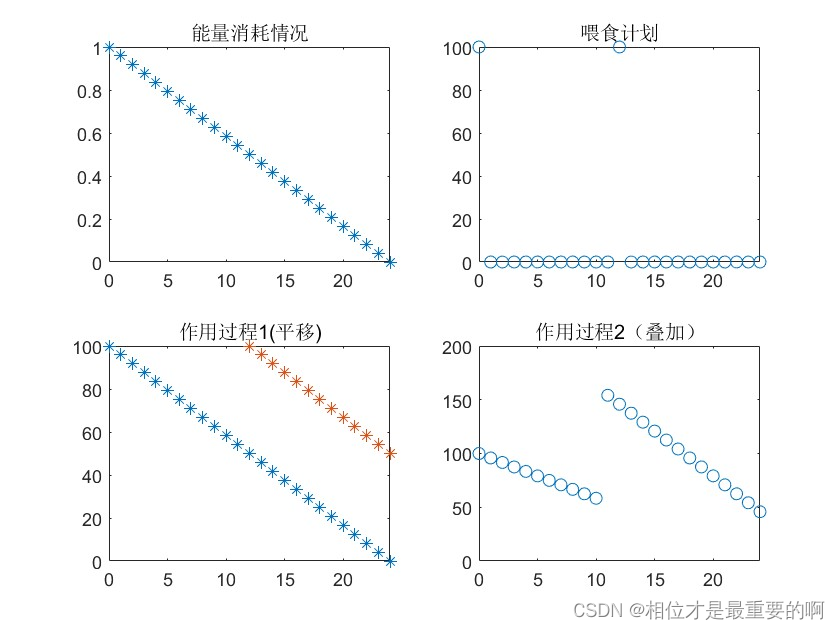对小狗来说：

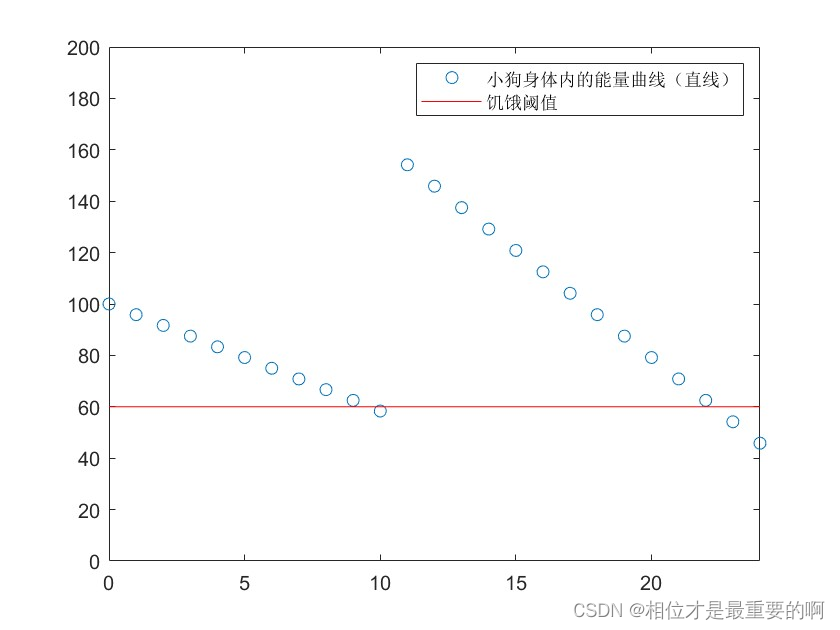卷积适用于所有类似于上面两种情况的场景，我也只是抛砖引玉，相信大家之后在学习卷积的过程中，能够想到更好的应用场景，用卷积对具体场景进行建模分析。

延伸阅读：信号与系统中的卷积

读者知识背景：信号与系统（傅里叶变换，卷积，基尔霍夫定律）

在本科学习的信号《信号与系统》中，用傅里叶分析的办法求解电路的输出常常是教学和考试中的重点。在看完本文之后，再来看看他们是怎么回事吧。

在上面的电路图中，你可以通过基尔霍夫定律写出电路的微分方程，然后通过傅里叶分析或者经典解法求得最汇总电路的输出 $u_R\left( t \right)$ 。

让我们来回顾一下傅里叶分析的办法，我们先是写出电路的微分方程，即：

$i_S\left( t \right) ={Cu_R}^{'}\left( t \right) +\frac{u_R\left( t \right)}{R}$

带入数值后是：

$i_S\left( t \right) =0.5\times {u_R}^{'}\left( t \right) +u_R\left( t \right)$

之后等式两边同时进行傅里叶变换（FT）得到：

$I_S\left( jw \right) =0.5jwU_R\left( jw \right) +U_R\left( jw \right)$

随后求出频率响应函数：

$H\left( jw \right) =\frac{U_R\left( jw \right)}{I_S\left( jw \right)}=\frac{1}{0.5jw+1}=\frac{2}{jw+2}$

再进行傅里叶逆变换（IFT）得到：

$h\left( t \right) =2e^{-2t}\varepsilon \left( t \right)$

而输入和输出在频域的关系是：

$I_S\left( jw \right) H\left( jw \right) =U_R\left( jw \right)$

在时域的关系是：

$i_S\left( t \right) *h\left( t \right) =u_R\left( t \right)$

现在，给了你任何输入，你都可以通过以上这些公式求出输出了，在这个电路图中，他们的关系是保持不变的。

通常情况下，为了避免卷积运算（因为计算比较复杂），我们会利用卷积定理将时域中的卷积转化到频域中的乘积进行计算。而 $H\left( jw \right)$ 被称为频率响应函数， $h\left( t \right)$ 是冲激响应函数。

现在，我们来思考一个问题，这个 $h\left( t \right)$ 究竟是什么？为什么输入和它卷积就是输入？

答案就在它的名字之中—冲激响应函数。

我们可以这样理解 $h\left( t \right)$ 当输入将输入信号分割为无穷多份，每份的时间大小是无穷小（类似于微积分的那种感觉）。那么，每无穷小，每单位强度（也就是输入的量纲，抱歉我不知道该怎么描述了）的输入，就会输出一个 $h\left( t \right)$ 。

那么考虑输出就是：第一时刻，第一时刻的输出=第一时刻的输入强度 $\times h\left( t \right)$ 。第二时刻，第二时刻的输出=第二时刻的输入强度 $$$ \times h\left( t \right) +$ 第一时刻的输入在第二时刻的输出……

可能你已经察觉了，这个 $h\left( t \right)$ 起到的作用，就是上文中的艾宾浩斯遗忘曲线，这正符合我们上文对于卷积的解释。对于单位强度的输入，都会有一个 $h\left( t \right)$ 输出， $h\left( t \right)$ 会随着时间的变化而变化，叠加到后边的时刻里（背过的单词会逐渐遗忘，记住的单词会累加到后边的天数之中）。

接下来的问题是：为什么我刚说，名字本身就是上个问题的答案（关于这个问题的答案不一定正确，但是你可以这样理解）？

信号与系统中介绍了一个实际上并不存在的冲激函数，即狄拉克函数，即 $\delta \left( t \right)$

，它的长度是无穷小，高度是无穷大，（时域上负无穷到正无穷的）积分是1。那么，我现在想进行上面所说的，把输入分成无穷多份，每份的区间长度是无穷小，单位强度是1，要怎么操作？

答案就是和冲激函数作用（之后我会用 $x\left( t \right)$ 表示输入， $y\left( t \right)$ 表示输出）。

冲激函数有下面的性质：

$$$ x\left( t \right) \times \delta \left( t \right) =x\left( 0 \right) \times \delta \left( t \right) \\ \int\limits_{-\infty}^{\infty}{x\left( t \right) \times \delta \left( t \right) dt=x\left( 0 \right)}$

把输入函数和冲激函数放到同一张图上就是：

首先， $$$ \delta \left( t \right)$ 本身的区间长度就是无穷小，相乘之后，也就可以取到输入函数 $$$ x\left( t \right)$ 任意时刻的值（只要将 $$$ \delta \left( t \right)$ 平移就好）。接下来， $$$ \delta \left( t \right)$ 与 $$$ x\left( t \right)$ 乘之后的积分为1，也就保证他是单位强度了。这时候对应的输出，就是 $$$ h\left( t \right)$ 。

那么，我们来考虑信号与系统中，最最经常让求的输出--阶跃响应。

$$$ \varepsilon \left( t \right) *h\left( t \right) =y\left( t \right)$

这是什么意思？

我仍然可以类比之前的单词计划，也就是：我从0时刻开始输入了单位强度为1的连续信号，强度大小始终保持不变，我制定了单词计划，从今天开始每天都背一个单词。而且知道了冲激响应 $$$ h\left( t \right)$ ，我知道了每背一个单词，单词随时间的遗忘速度（艾宾浩斯遗忘曲线）。那 $$$ y\left( t \right)$

用上边的公式表达就是很清楚的事情了，因为卷积本身就是适用于这种情况（线性时不变系统，每次输入得到的输出都不会立刻消失，而是会变化一些于之后时刻的输入的输出）。唯一的差别是就是：我们之前的背单词计划是离散状况，而在电路图的输入和输出通常是连续状况。不过，正如我所说，离散序列的卷积和和连续状况的卷积表达的是同一个意思。

一点无关紧要的话：

看完本文，我想你对卷积是什么，在什么情况下用，为什么要进行卷积这些问题已经很清楚了。如果你有一点点的收获，我都没有白白在期中考试周另外抽出十几个小时写完这篇文章。

我一直都觉着，学习只是本身并不是为了知道它怎么算，而是要理解它的意义，在说什么情况下用。我仍然记得在高一刚刚学指数函数的时候，我对于e这个常数感到十分困惑。如果你只是告诉我，e=2.718……，我不会甘心的。但是如果你举几个例子说明，e是自然界中存在的常数（比如有关银行利率的事情），当时的我可能会对自然底数这个奇奇怪怪的无理数有一些认识。当然，就算当时只告诉你e是一个无理数，随着后边知识的学习，你也会明白e究竟为什么是自然常数，就像明白 $$$ \pi$ 一样。只是，我觉得，是不是这个认识可以提前一点点，哪怕很少……

事的开始是因为，我在刚刚学卷积的时候，对于卷积能够干什么，什么情况下做卷积这个问题感觉到很疑惑，然而我当时查了很久的资料都没有查到我想要的内容（可能有，但是我没找到吧）。2023年4月18日中午，躺在床上睡午觉的我突然想起这件事情，我认为，现在的我应该已经能够回答这个问题了，于是我就从床上跳下来，开始写这篇文章。我之前学习其他课程的时候还有很多很多想法，不过这次是我第一次以博客的方式写出来。实际过程比我想象的要难很多（是我太菜了），也比我想象中花的时间要多得多，matlab有段时间没用了，也觉得有些生疏了。网上搜到的艾宾浩斯遗忘曲线在0之前的图像是异常的，直接平移不行，怎么得到预期的效果……

当然最后一一解决了，所以才有了这个文章。要说目的的话，可能是希望下一个像我一样的人（也就是你们）能够找到他想找到的资料。额，现在，我现在该担心担心我两门课的期中考试怎么办了……

我的文笔并不好，也许有的地方没有表达清楚，作图的字迹也很潦草，感谢大家能够看到这。

当然这其中最最重要的部分是老师和同学的帮助。为了让本文错误更少，达到我预想的效果，我找了我没学过卷积的同学当第一批读者，我非常非常感谢他们。

祝看到本文的人天天开心！

小豪同学

2023年4月23日