【数模-评价类模型】层次分析法_评价层次模型图-CSDN博客

本文链接：https://blog.csdn.net/weixin_60279621/article/details/145103056

一、使用场景

适用场景：

评价类问题

局限性：

1）n不能过大，可能会导致一致性差异过大

2）已知标准/准则/指标的数据，则不使用

二、建模步骤

第一步：建立层次结构

评价类问题三问：

①我们评价的目标是什么？

②我们为达到这个目的可选方案？

③评价的标准/指标/准则是什么？

即根据评价类三问的目标、标准、方案搭建。

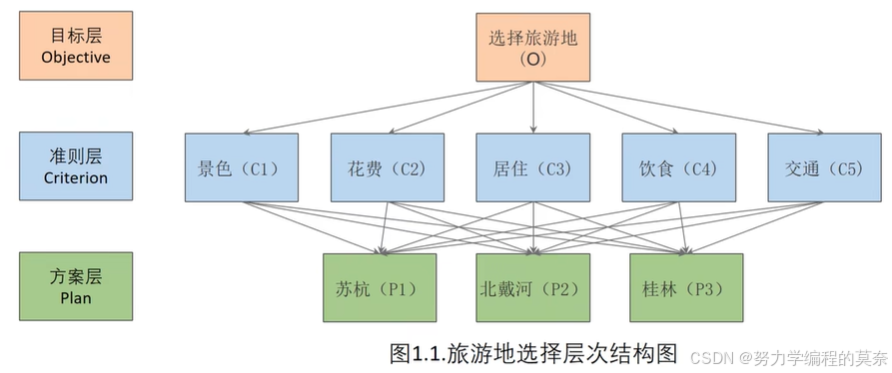
图片制作方式：PPT（Smartart）、Xmind……

第二步：构造各层次的判断矩阵

填的数值聚优主观性（比赛时只能自己填写/AI填写），理想状况为专家群体判断。

在论文中直接给出判断矩阵，不用说明是如何给出的。

PS：结合实际/联系材料信息

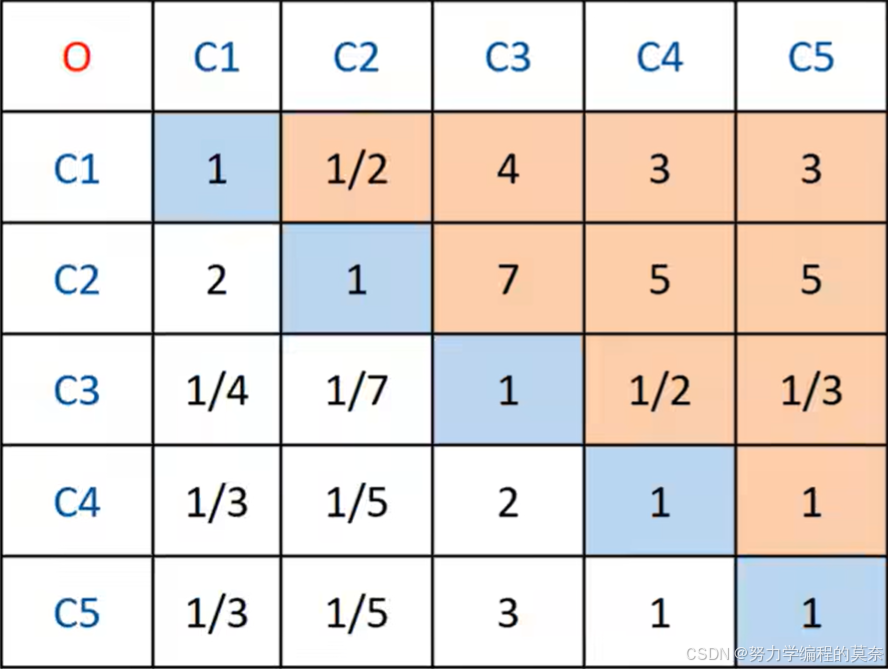
判断矩阵步骤：

Ⅰ）对指标进行两两比较，根据如下标准填写

Ⅱ）矩阵中 $a_{ij}$ 代表，i指标相对于j指标的重要程度

Ⅲ） $a_{ij} \times a_{ji}=1$

Ⅳ）两两比较可能会出现矛盾，需要通过一致性检验

一致矩阵：各行各列成倍数关系

第三步：对判断矩阵进行一致性检验

一致性检验步骤：

①计算一致性指标CI

$CI=\dfrac{{}\lambda_{max} -n}{n-1}$

其中 λ 为判断矩阵的最大特征值，n为方阵的大小

②查找对应RI

③计算一致性比例CR

$CR=\dfrac{CI}{RI}$

如果CR<0.1，则可认为判断矩阵的一致性可以接受，否则需要修正判断矩阵。

第四步：计算权重

三种计算权重的方法：

法一：算术平均法

a. 按列归一化，每个元素除以所在列之和

b. 每个指标在每一列的权重求平均

$W_i= \frac{1}{n} \sum_{j=1}^{n} \dfrac{a_{ij}}{\sum_{k=1}^{n} a_{kj}}$

法二：几何平均法

a. 矩阵中同一行的元素相乘

$M_i=\prod_{j=1}^{n} a_{ij}$

b. 对每行的乘积开n次方根

$Y_i=\sqrt[n]{M_i}$

c. 归一化处理，得到最后的权重

$W_i=\dfrac{Y_i}{\sum_{i=1}^{n}Y_i}$

法三：特征值法

a. 求出矩阵最大特征值，以及其对应的特征向量

b. 对特征向量进行归一化

建议三种方法都使用，来保证结果的全面、有效。

第五步：根据计算所得权重构建权重矩阵

对每一个方案的数值乘以权重，计算出最后结果，并对方案进行排序。

利用Excel计算更方便！

三、模型拓展

1）准则层可以有多个

2）准则层与方案层不一定要一一对应（未对应的视作0）

3）每个准则层对应不同的方案层

四、代码（Python）

1.一致性检验

import numpy as np

# 定义矩阵A
# np.array 用于创建数组。
A = np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,1/2],[1/5,1/2,2,1]]) # 原判断矩阵(手动输入)
n = A.shape[0] # 获取A的行，0变为1则是获取A的列，shape是获取形状信息
 
# 求出最大特征值以及对应的特征向量
# np.linalg.eig 用于计算方阵的特征值和特征向量。
eig_val,eig_vec = np.linalg.eig(A) # eig_val是特征值，eig_vec是特征向量
Maxeig = max(eig_val) # 求特征值的最大值
 
CI = (Maxeig-n)/(n-1)
ri = [0,0.0001,0.52,0.89,1.12,1.26,1.36,1.41,1.46,1.49,1.52,1.54,1.56,1.58, 1.59] 
RI = ri[n-1]
# 这里n=2时，一定是一致矩阵，所以CI =0，我们为了避免分母为0，将这里的第二个元素改为了很接近0的正数
 
CR = CI/RI
if CR< 0.10:
    print(CR,'通过一致性检验')
else:
    print(CR,'未通过一致性检验，请修改')

2.算数平均法求权重

import numpy as np
# 定义判断矩阵A
A = np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,2],[1/5,1/2,1/2,1]])
n = A.shape[0]

# 计算每列的和
# np.sum 用于计算一维数组中所有元素的总和。
# 在二维数组中，axis=0 表示按列计算总和，axis=1 表示按行计算总和。
ASum = np.sum(A, axis=0)

# 归一化
# 二维数组除以一维数组，会自动将一维数组扩展为与二维数组相同的形状，然后进行逐元素的除法运算。
stand_A = A/ASum
# 各列相加到同一行
ASumr = np.sum(stand_A, axis=1)
#计算权重向量
weights = ASumr/n
print('算术平均法求的权重结果为：',weights)

3.几何平均法求权重

import numpy as np
# 定义判断矩阵A
A = np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,2],[1/5,1/2,1/2,1]])
n = A.shape[0]

# 将A中每一行开素相乘得到一列向量
# np.prod 用于计算一维数组中所有元素的乘积。
prod_A = np.prod(A, axis=1)

# 将新的向量的每个分量开n次方等价求1/n次方
# np.power 用于对数组中的元素进行指数运算。
prod_n_A=np.power(prod_A, 1/n)

# 归一化处理
re_prod_A= prod_n_A/ np.sum(prod_n_A)
print('几何平均法求的权重结果为：',re_prod_A)

4.特征值法求权重

import numpy as np

A = np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,2],[1/5,1/2,1/2,1]])
n = A.shape[0]

# 求出特征值和特征向量
eig_values,eig_vectors = np.linalg.eig(A)

# 找出最大特征值的索引
# np.argmax 用于返回数组中最大值的索引
max_index = np.argmax(eig_values)

# 找出对应的特征向量
max_vector = eig_vectors[:, max_index]

# 对特征向量进行归一化处理,得到权重
weights = max_vector /np.sum(max_vector)
print('特征值法求的权重结果为：',weights)

注意：在代码中可以将以上内容写成函数的形式调用