【数模—相关性模型】相关系数_皮尔逊相关系数模型-CSDN博客

本文链接：https://blog.csdn.net/weixin_60279621/article/details/145163362

一、适用场景

衡量两个变量之间相关性的大小，根据数据满足的不同条件选择不同的相关系数计算分析。

二、Pearson建模

总体：考察样本的全部个体

样本：总体中抽取部分个体

总体皮尔逊Pearson相关系数

X、Y是两组总体数据 X：{X1，X2……Xn} Y：{Y1，Y2……Yn}

总体均值 $E\left ( x \right )=\dfrac{\sum_{i=1}^{n}X_i}{n}$ $E\left ( x \right )=\dfrac{\sum_{i=1}^{n}Y_i}{n}$

总体协方差 $Cov\left ( X,Y \right )=\dfrac{\sum_{i=1}^{n}\left ( X_i -E\left ( X \right )\right )\left ( Y_i-E\left ( Y \right ) \right )}{n}$

注意：协方差的大小和两个变量的量纲有关，因此不适合作比较。

标准差 $\sigma _x=\sqrt{\dfrac{\sum_{i=1}^{n}\left( X_i-E\left ( X \right )\right)^2}{n}}$ $\sigma _y=\sqrt{\dfrac{\sum_{i=1}^{n}\left( Y_i-E\left ( Y \right )\right)^2}{n}}$

总体Pearson相关系数 $\sigma _{xy}=\dfrac{Cov\left ( X,Y \right )}{\sigma_x \sigma_y }$

$\left | \sigma _{xy} \right |\leq 1$ 且当 Y=aX+b 时， $\sigma _{xy}=1/-1$

Pearson相关系数可以看成剔除了变量量纲影响，X和Y标准化后的协方差

样本Pearson相关系数

X、Y是两组总体数据 X：{X1，X2……Xn} Y：{Y1，Y2……Yn}

总体均值 $\bar{X}=\dfrac{\sum_{i=1}^{n}X_i}{n}$ $\bar{Y}=\dfrac{\sum_{i=1}^{n}Y_i}{n}$

总体协方差 $Cov\left ( X,Y \right )=\dfrac{\sum_{i=1}^{n}\left ( X_i -\bar{X}\right )\left ( Y_i-\bar{Y} \right )}{n-1}$

注意：协方差的大小和两个变量的量纲有关，因此不适合作比较。

标准差 $S _x=\sqrt{\dfrac{\sum_{i=1}^{n}\left( X_i-\bar{X}\right)^2}{n-1}}$ $S _y=\sqrt{\dfrac{\sum_{i=1}^{n}\left( Y_i-\bar{Y}\right)^2}{n-1}}$

总体Pearson相关系数 $\gamma _{xy}=\dfrac{Cov\left ( X,Y \right )}{S_x S_y }$

注意：只有在两个变量线性相关的情况下，皮尔逊相关系数才能表现相关性。

易错点：

1）非线性相关也会导致线性相关系数很大

2）离群点对相关系数的影响很大

3）如果两个变量的相关系数很大也不能说明两者相关，可能是受到了异常值的影响。

4）相关系数计算结果为0，只能说不是线性相关，但说不定会为非线性相关

相关性	负	正
无相关性	-0.09~0.0	0~0.9
弱相关性	-0.3~--0.1	0.1~0.3
中相关性	-0.5~-0.3	0.3~0.5
强相关性	-1.0~-0.5	0.5~1.0

比起相关系数大小，我们更关注显著性（假设检验）

假设性检验

第一步：确定原假设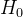 $H_0$ 和备择假设 $H_1$

$H_0H_1$ 是恰好相反的两面。

第二步：在原假设成立条件下构造分布

分布：正态分布、t分布、F分布、 $x^2$ 分布

正态分布 W~N(均值，方差）

皮尔逊相关系数构造 $t=\gamma \sqrt{\dfrac{n-2}{1-\gamma ^2}}$

第三步：画出分布的概率密度图

概率密度函数性质

1) $f\left ( x \right )\geq 0$

2） $\int_{-\infty }^{+\infty }f\left ( x \right )dx=1$

正态分布概率密度函数 $f\left ( x \right )= \dfrac{1}{\sqrt{2}}e^{-\frac{x^2}{2}}$

第四步：给一个置信水平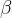 $\beta$ （相信原假设成立的概率）

置信水平： $\beta =1-\alpha$ （一般为90%、95%、99%）

显著性水平 $\alpha$ ：拒绝原假设的概率

第五步：用已知样本数据代入计算统计量

P值判断法

单侧检验p( $x\leq x_0$ )=F( $x_0$ )

双侧检验p=2倍的单侧检验

p>0.01	在99%的置信水平无法拒绝原假设
p>0.05	在95%的置信水平无法拒绝原假设
p>0.10	在90%的置信水平无法拒绝原假设

皮尔逊相关系数假设检验条件：

        1. 实验数据通常假设是成对的来自于正态分布的总体。
        2. 实验数据之间的差距不能太大。
        3. 每组样本之间是独立抽样的。

*正态分布假设性检验

三、spearman建模

X和Y为两组数据

斯皮尔曼相关系数 $r_s=1-\dfrac{6\sum_{i=1}^{n}d_i^2}{n\left ( n^2-1 \right )}$

其中d为XY的等级差（等级：一列数从小到大排列，这个数所在位置）

注意：当数值相同时，取他们所在位置的算术平均。

小样本情况：n<30

直接查表

大样本情况

构造检验值 $r_s\sqrt{n-1}\sim N\left ( 0,1 \right )$

求出对应的p值，与0.05相比较即可

四、总结

斯皮尔曼相关系数和皮尔逊相关系数选择:

1.连续数据，正态分布，线性关系，用pearson相关系数是最恰当，当然用spearman相关系数也可以，就是效率没有pearsoh相关系数高。

2.上述任一条件不满足，就用spearman相关系数，不能用pearson相关系数

3.两个定序数据之间也用spearman相关系数，不能用pearson相关系数。

定序数据：仅仅反映观测对象等级、顺序关系的数据，是由定序尺度计量形成的，表现为类别，可以进行排序，属于品质数据。