求微分方程的近似解在实际问题的解决中具有极其重要的作用,因为在大多情况下我们很难求出微分方程的函数表达式,或是表达式过于复杂,此时便可以用数值计算的方法求该微分方程的近似解。欧拉法便是其中一种最为简单的求常微分方程近似解的方法,该方法较为简单,同时也有比较明显的缺陷,但也是其它的求解微分方程近似解方法的基础。
算法原理
欧拉法求解过程是一个递归的过程,这个思想和牛顿法、梯度下降法是相似的。并且它将函数离散化,分割成一个个小段来求解。欧拉法求解的常微分方程的形式通常为:
右边是关于x,y的任意函数,如2x,3y+2或等都是可以的,但y是x的函数,并且函数定义在区间[a,b]内,初值条件为x=a时函数值为
。欧拉法求解思想是把区间[a,b]分成n份,那么每一小段长度就是
,初始时左端点a=x0,那么下一个节点x1=x0+h,再下一个就是x2=x1+h,......以此类推,最后
=b。我们对上面的微分方程两边同时从
到
进行积分,就得到下面结果,即:
这样便可以由初始条件y(x0)=与该条件式逐个递推,依次求得y(x1),y(x2)...y(xn)各个函数值。对于右端的积分,在实际计算过程中也需要用近似表达式来替代。欧拉法使用的是由矩形面积来近似替代,即:
这样我们就得到了最终的递归表达式:
从而能够比较简便地进行计算。
算法实现
兔兔这里以一个微分方程为例:
对应前面的表达式,这里,所以计算过程为
,并且x0=0,y0=1,之后再求解y2,y3...yn。h根据需要可以做不同调整,如果h=0.1就是分10份,h越小,分的份数越多,点越来越密集,就可以体现函数的形式。
import numpy as np
import matplotlib.pyplot as plt
y0=1 #初始条件
def f(x,y):
return y-2*x/y
def Eular(y0,n,f):
y=[y0] #储存各个点的函数值
y0=y0
for x in np.linspace(0,1,n):
'''求函数在区间[0,1]近似解,分n份'''
y1=y0+f(x,y0)/n
y.append(y1)
y0=y1
return y
y=Eular(1,10,f=f)
x=np.linspace(0,1,len(y))
plt.plot(x,y,color='blue')
plt.show()该函数是=的精确解为,我们最终把精确解,n=10,n=100的结果进行比较,图像如下所示:
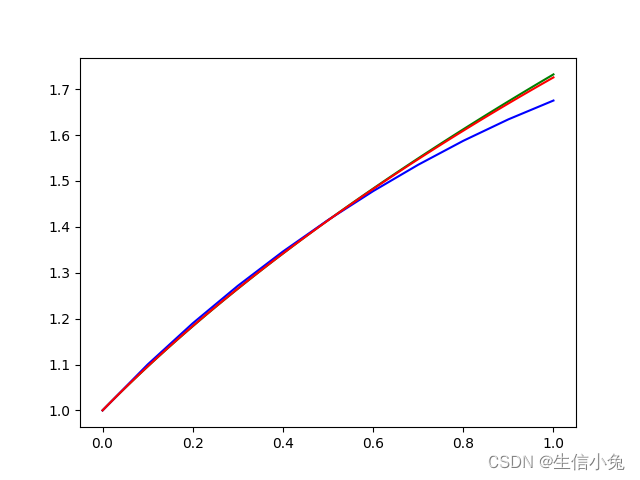
其中绿色的是精确解,红色对应的n=100,蓝色为n=10,我们发现结果比较接近,并且随着n的增加近似效果也有所提高。但是该方法也有缺点,就是随着计算步数增加误差逐渐增多,并且误差也是比较大的。原因之一是欧拉法是一种一阶方法,其局部阶段误差也是比较大的,其再节点局部阶段误差为:
所以为了减少误差,就需要其它的一些方法,如改进欧拉法,龙格-库塔法等。
总结
欧拉法作为微分方程近似解的一种求解方法,无论是其数值计算的思想还是对于实际问题的解决都是有重要意义的,但欧拉法的问题也是值得注意的,因此在欧拉法的基础上发展其它精度更高的方法是十分必要的。

























 3288
3288

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










