树的应用——堆

---

引子

优先队列
“优先队列” （Priority Queue），是一种特殊的“队列”，从队中取出元素的顺序是依照元素的优先权（关键字）大小，而不是元素进入队列的先后顺序。

利用数组或链表实现优先队列，则：
数组：
插入：元素总是插入尾部 — O(1)
删除：查找最大（最小）的关键字 —O(n)，从数组中删去需要移动元素—O(n)
有序数组
插入：找到合适的位置—O(n)orO(log2n)，移动元素并插入—O(n)
删除：删去最后一个元素—O(1)
链表
插入：元素总是插入链表的头部—O(1)
删除：查找最大（最小）的元素—O(n)，删除元素—O(1)
有序链表
插入：找到合适的位置—O(n)，插入元素—O(1)
删除：删去首元素—O(1)
总的来讲，上述方法插入或删除操作至少有一个达到线性时间复杂性。

有没有一种实现方式，能使优先队列的插入删除操作时间复杂度都低于O（n）呢？——为此，引入堆的概念

---

一、堆的定义

• 采用完全二叉树存储的优先队列，称为堆(Heap)。
  体现出堆的的特性：
  结构性：完全二叉树；
  有序性：根结点到任一结点的关键字序列保持非递增或者非递减。

常见的堆可分为最大堆（大根堆，大顶堆），最小堆（小根堆，小顶堆）
其中最大堆的定义：一个有N>0个元素的最大堆H是一棵完全二叉树，每个结点上的元素值不小于其子结点元素的值。

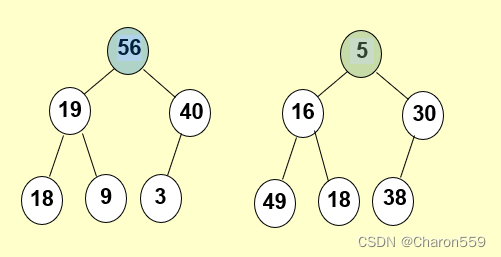
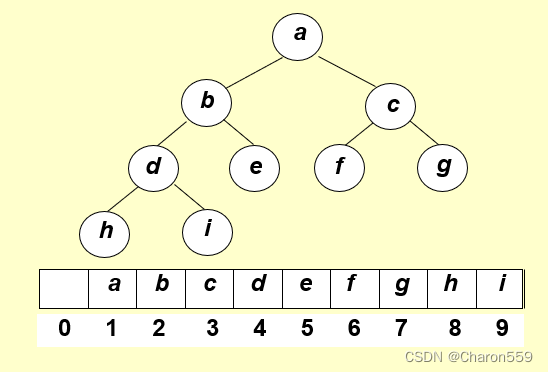
存储方式： 由于堆是一棵完全二叉树，因此，通常不必用链式存储，常用数组进行存储实现。（数组下标为0的地方通常不用来存储堆的结点。）

二、最大堆的操作

1.ADT

类型名称：最大堆（MaxHeap）
数据对象集：一个有N>0个元素的最大堆H是一棵完全二叉树，每个结点上的元素值不小于其子结点元素的值。
操作集：对于任意最多有MaxSize个元素的最大堆H ∈ MaxHeap，元素item ∈ ElementType，主要操作有：
MaxHeap Create( int MaxSize )：创建一个空的最大堆。
Boolean IsFull( MaxHeap H )：判断最大堆H是否已满。
Insert( MaxHeap H, ElementType item )：将元素item插入最大堆H。
Boolean IsEmpty( MaxHeap H )：判断最大堆H是否为空。
ElementType DeleteMax( MaxHeap H )：返回H中最大元素(高优先级)

2.操作集

结构定义

typedef struct HeapStruct *MaxHeap;
struct HeapStruct{
	ElementType *Elements/*存储堆元素的数组*/
	int Size;			 /*当前元素的个数*/
	int Capacity;		 /*堆的最大容量*/
	
}

创建一个空的最大堆

MaxHeap Create(int Maxsize){
	MaxHeap H = malloc(sizeof(struct HeapStruct));
	H->Elements = malloc((Maxsize+1)*sizeof(Elements));
	H->Size = 0;
	h->Capacity = MaxSize;
	H->Elements[0] = MaxData;
	/*定义“哨兵”的值大于堆中所有可能元素，以便后续操作*/
	return H;
}

把MaxData换做MinData，则同样适用于最小堆的创建

最大堆的插入

最大堆的插入，前提必须满足完全二叉树的结构要求，即插在数组的末尾。所以插入操作需要做的就是确保堆的有序性
算法描述: 要插入的元素向上渗透。即只要大于其父结点关键字，就渗透成功，与父结点交换关键字，直到渗透失败为止。

void Insert(MaxHeap H,ElementType item){
	int i;
	if(IsFull(H)){
		printf("最大堆已满");
		return ;
	}
	i = ++H->Size;/*i指向符合结构要求的位置*/
	for(;H->Elements[i/2]<item;i/=2){
	/*H->Elements[0]是哨兵元素，它不小于堆中的最大元素，控制循环结束。*/
		H->Elements[i] = H->Elements[i/2];/*向上渗透*/
	}
	h->Elements[i] = item;/*插入*/
}

T(N) = O(logN)

最大堆的删除

算法描述： 取出根结点（最大值）元素，同时将最后一个结点移动到根结点位置。用该根结点向下渗透，调整堆使其有序。

ElementTyoe DeleteMax(MaxHeap H){
/*从最大堆H中取出键值为最大的元素，并删除一个结点*/
	int Parent,Child;
	ElementType MaxItemm,temp;
	if(IsEmpty(H)){
		printf("最大堆已为空");
		return;
	}
	MaxItem = H->Elements[1];/*取出根结点最大值*/
	/*用最大堆中最后一个元素从根结点开始向下渗透*/
	temp = H->Elements[H->Size--];/*暂存并删除最后一个元素*/
	for(Parent = 1;Parent*2 <= H->Size;Parent=Child){
		Child = Parent * 2;
		if(Child!=H->Size)&&(H->Elements[Child]<H->Elements[Child+1])
			Child++;/*Child指向左右结点的较大者*/
		if(temp >= H->Elments[Child]) break;
		else H->Elements[Parent] = H->Elements[Child];/*向下渗透*/
	}
	H->Elements[Parent] = temp;
	return MaxItem;
	
	
}

T(N) = O(logN)

最大堆的建立

“建立最大堆”是指如何将已经存在的N个元素按最大堆的要求存放在一个一维数组中。
通过最大堆的插入操作，将N个元素一个个相继插入到一个初始为空的堆中去，其时间代价最大为O(N logN)。
有无更快的方法？——
第一步，将N个元素按输入顺序存入二叉树中，这一步只要求满足完全二叉树的结构特性，而不管其有序性。
第二步，调整各结点元素，以满足最大堆的有序特性。

MaxHeap BuildMaxHeap(MaxHeap H){
	/*H->Size个元素已经存在H->Elements[]中，此函数做元素调整，以满足最大堆的有序性*/
	int Parent,Child,i;
	ElementType temp;
	for(i = H->Size/2;i>0;i--){
	/*从最后一个结点的父结点开始向下渗透*/
		temp = H->Elements[i];/*父结点值*/
		for(Parent=i;Parent*2<=H->Size;Parent=Child){
		/*向下渗透*/
			Child = Parent * 2;
        	if( (Child!= H->Size) && (H->Elements[Child] < H->Elements[Child+1]) )
        	    Child++;  /*Child指向左右子结点的较大者*/
        	if( temp >= H->Elements[Child] ) break;
   			else  /* 渗透成功*/
       	   H->Elements[Parent] = H->Elements[Child];
  		} /* 结束内部for循环对以H->Elements[i]为根的子树的调整 */
 		 H->Elements[Parent] = temp;
	}
	return H;
}