【改进灰狼算法】基于记忆、进化算子和局部搜索的改进灰狼优化算法及线性种群规模缩减算法（Matlab代码实现）-CSDN博客

本文链接：https://blog.csdn.net/weixin_61181717/article/details/146114545

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、文章下载

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

摘要
多模态函数的优化即使对于进化算法和基于群体的算法来说也是一个挑战，因为它需要高效地探索以找到有希望的搜索空间区域，并有效地利用以精确找到全局最优解。灰狼优化器（Grey Wolf Optimizer, GWO）是一种最近开发的受自然启发的元启发式算法，参数调整相对较少。然而，GWO及其大多数变体可能面临种群多样性不足、早熟收敛以及无法在探索和利用行为之间保持良好平衡的问题。为了解决这些限制，本研究提出了一种新的GWO变体，结合了记忆、进化算子和随机局部搜索技术，并进一步整合了线性种群规模缩减（Linear Population Size Reduction, LPSR）技术。所提出的算法在23个数值基准函数、高维基准函数、13个工程案例研究、四个数据分类和三个函数近似问题上进行了全面测试。基准函数大多取自CEC 2005和CEC 2010特别会议，包括旋转和移位函数。工程案例研究来自CEC 2020的实际非凸约束优化问题。所提出的GWO的性能与流行的元启发式算法进行了比较，包括粒子群优化（Particle Swarm Optimization, PSO）、引力搜索算法（Gravitational Search Algorithm, GSA）、拍击群体算法（Slap Swarm Algorithm, SSA）、差分进化（Differential Evolution, DE）、自适应差分进化（Self-adaptive Differential Evolution, SADE）、基本GWO及其三个最近改进的变体。进行了统计分析和Friedman检验以彻底比较它们的性能。所获得的结果表明，所提出的GWO在基准函数和工程案例研究的测试中优于比较的算法。

**1. 引言**
受自然启发的元启发式算法因其全局搜索能力和避免局部最优的能力而变得非常流行，而无需任何关于优化问题中函数的梯度和可微性的信息[1–3]。它们通常被视为随机全局优化器，在搜索中使用随机数，涉及少量参数，且易于应用[4,5]。流行的元启发式算法包括遗传算法（Genetic Algorithm, GA）[6]、模拟退火（Simulated Annealing, SA）[7]、粒子群优化（Particle Swarm Optimization, PSO）[8]、差分进化（Differential Evolution, DE）[9]和蚁群优化（Ant Colony Optimization, ACO）[10]。
自2005年以来开发的一些流行的元启发式算法包括人工蜂群（Artificial Bee Colony, ABC）算法[11]、大爆炸-大挤压（Big Bang-Big Crunch, BBBC）[12]、中心力优化（Central Force Optimization, CFO）[13]、黄蜂群体算法[14]、布谷鸟搜索（Cuckoo Search, CS）[15]、引力搜索算法（Gravitational Search Algorithm, GSA）[16]、蝙蝠算法（Bat Algorithm, BA）[17]、萤火虫算法（Firefly Algorithm, FA）[18]、磷虾群[19]、黑洞（Black Hole, BH）算法[20]、灰狼优化器（Grey Wolf Optimizer, GWO）[21]、蜻蜓算法（Dragonfly Algorithm, DA）[22]、鲸鱼优化算法（Whale Optimization Algorithm, WOA）[23]、电搜索算法（Electro-search Algorithm, ESA）[24]和哈里斯鹰优化器（Harris Hawk Optimizer, HHO）[25]、人工化学反应优化算法[26]和战争策略优化算法[27]。
文献中现有的元启发式方法被分为九个不同的组，即基于生物学、物理学、群体、社会、音乐、化学、体育、数学和混合方法（这些方法的组合）[27,28]。最受欢迎的元启发式算法可以分为三组，即（a）进化算法（例如GA和DE）、（b）群体智能（例如PSO、ACO和GWO）和（c）基于物理学的算法（例如GSA和BH），如图1所示[29]。其中，群体智能算法的灵感来源于神经科学、社会动物学、行为科学和/或认知心理学[30]，并模仿自然中生物生物的智能行为[31]。它们具有自组织、并行性、灵活性、分布性和鲁棒性的优越特性，并被用于解决各种优化问题，例如与电力系统[32]、制冷系统[33]、通信网络[34]、模糊系统控制[35]、人工神经网络训练[36]、参数估计[37]、金融时间序列预测[38]、机器人控制[39]、图像处理[40]、甲酸生产[41]、间歇萃取蒸馏[42]、井筒轨迹设计中的不确定性处理[43]、电火花加工过程优化[44–48]。
许多元启发式算法具有快速收敛和简单性等优点。然而，这种高收敛速度、随机性和简单性往往导致多样性的丧失和早熟收敛。这些问题促使研究人员开发和研究新方法，通过多种方法更新位置（即试验解），以快速找到可行解空间，摆脱局部最优陷阱，并处理在群体（或种群）内保持多样性以及促进搜索中的探索问题。
群体智能技术通过混合、自适应参数调整和在算法中增加新步骤等策略在文献中得到了改进。其中一些例子包括：将差分进化的变异操作引入蚁群优化以进行信息素试验[49]、具有PSO的局部和全局概念的人工蜂群算法[50,51]、具有交叉和变异的PSO[52]、自适应差分进化（JADE）算法[53]、自适应差分进化（SaDE）算法[54]、将差分进化的变异和交叉操作引入无参数裸骨PSO[55]和具有生态位的PSO[2]。
关于通过这些策略修改GWO的文献在随后的段落中讨论。

**2. 背景**
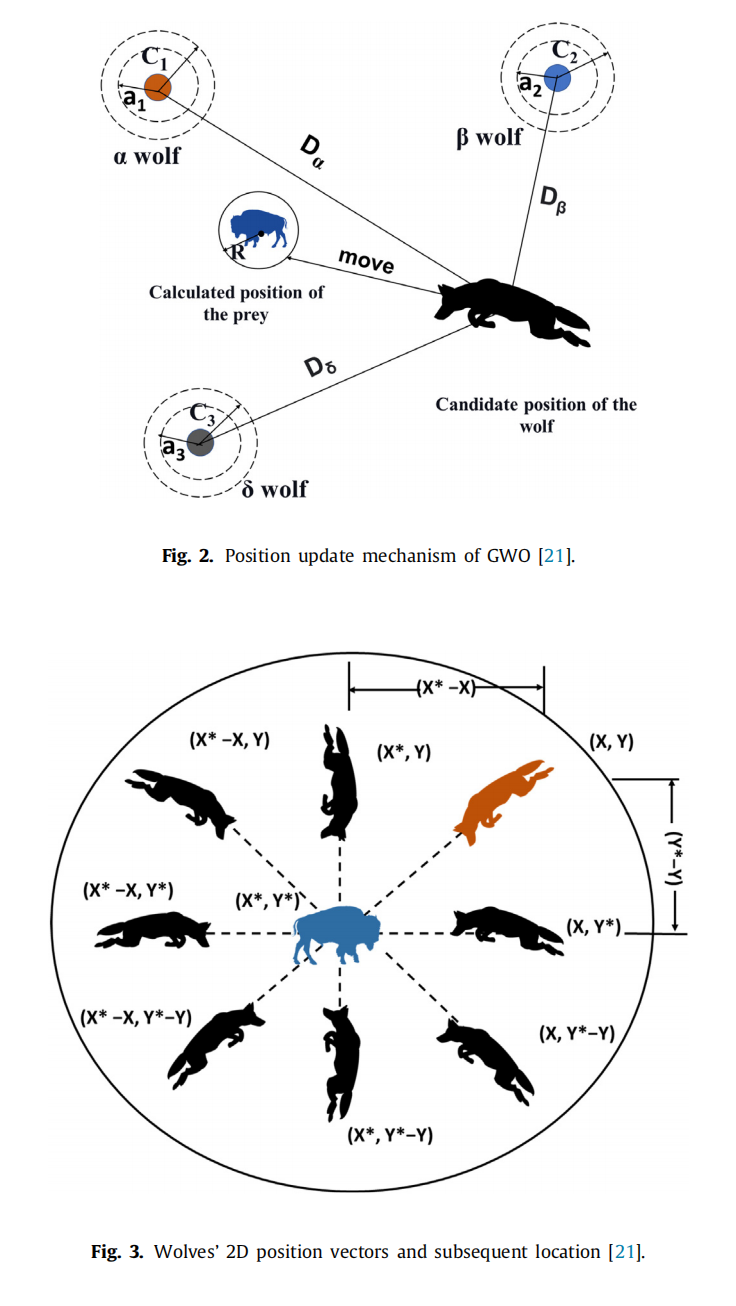
GWO是由Mirjalili等人[21]于2014年开发的一种新颖的群体智能算法，基于狼的社会领导层次和它们的集体狩猎行为。由于其简单性、非常少的控制参数和更好的搜索精度，该算法在工程领域的应用中受到了广泛关注[30,52]。例如，GWO已成功应用于最优潮流[56]、参数估计[57]、特征选择[58]、风速预测[59]、经济调度[60]、模式识别[61]、大规模机组承诺[62]、光伏阵列的最优设计[63]、PI-PD控制器[64]和井筒轨迹优化[65]。自其诞生以来，已经提出了几种GWO变体，并应用于不同领域[66]。基于进化种群动态（Evolutionary Population Dynamics, EPD）的GWO，称为GWO-EPD，由Saremi等人[67]提出，其中EPD将弱代理重新定位到GWO的最佳解（alpha、beta和delta）附近。它还重新初始化最差的狼，以在每次迭代中保持狼群之间的多样性，并进一步提高算法的探索能力。GWO-EPD为大多数基准函数提供了比基本GWO更好的数值结果。Jayabarathi等人[60]提出了混合GWO（HGWO），带有交叉和变异，以解决非凸、无约束和约束的经济调度问题。他们声称他们的方法在四个案例研究（在不同运行条件下，分别有6、15、40和80个发电机）中表现出了有希望的性能。王和李[31]建议了另一种GWO变体，其中包括差分进化的交叉和变异算子。此外，他们的GWO中还包括了适者生存的淘汰机制，以去除最差的狼。在每次迭代中，随机生成相同数量的新狼来替换最差的狼。最近，Saxena等人[68]开发了智能GWO（Intelligent Grey Wolf Optimizer, IGWO），这是一种带有交叉、变异、选择和正弦桥接机制的GWO变体，用于解决电力网络的谐波估计设计。他们验证了该算法在CEC 2017的30个基准函数和2个谐波估计案例研究中的性能；所提出的算法为基准函数提供了具有竞争力（即更好或相当）的结果，并在大多数文献案例研究中优于其他算法。
关于采用不同技术改进基本GWO的文献如下。Malik等人[69]推荐了另一种GWO版本，其中狼的当前位置是基于狼之间的加权距离而不是使用三只领导狼的平均位置来更新的。Guha等人[70]开发了基于准对立学习的GWO（Quasi-oppositional based learning Grey Wolf Optimizer, QOGWO）；这些作者使用QOGWO设计了最优PID控制器，以控制两个

📚2 运行结果

部分代码：

%% GREY WOLF OPTIMIZER PART 

while FE < Max_FE
    for i=1:Agents_no
        
        % Checking boundaries 
        Agents(i).Position = max(Agents(i).Position,lb);
        Agents(i).Position = min(Agents(i).Position,ub);
        Agents_Position_Memory(i,:) = max(Agents_Position_Memory(i,:),lb);
        Agents_Position_Memory(i,:) = min(Agents_Position_Memory(i,:),ub);
        
        % Update Alpha, Beta, and Delta from the Explorer swarm 
        if Agents(i).fitness < Alpha_score
            Alpha_score = Agents(i).fitness; % Update alpha
            Alpha_pos = Agents(i).Position;
        end
        
        if Agents(i).fitness > Alpha_score && Agents(i).fitness < Beta_score
            Beta_score = Agents(i).fitness; % Update beta
            Beta_pos = Agents(i).Position;
        end
        
        if Agents(i).fitness > Alpha_score && Agents(i).fitness > Beta_score && Agents(i).fitness < Delta_score
            Delta_score = Agents(i).fitness; % Update delta
            Delta_pos = Agents(i).Position;
        end
    end
    
    a=2-l*((2)/Max_iter); % a decreases linearly fron 2 to 0
    
    % Update the Position of search agents including omegas
    for i=1:Agents_no
        
        r1=rand(); % r1 is a random number in [0,1]
        r2=rand(); % r2 is a random number in [0,1]
        
        A1=2*a*r1-a; % Equation (3.3)
        C1=2*r2; % Equation (3.4)
        
        D_alpha=abs(C1*Alpha_pos-Agents(i).Position); % Equation (3.5)-part 1
        X1=Alpha_pos -A1*D_alpha; % Equation (3.6)-part 1
        
        r1=rand();
        r2=rand();
        
        A2=2*a*r1-a; % Equation (3.3)
        C2=2*r2; % Equation (3.4)
        
        D_beta=abs(C2*Beta_pos-Agents(i).Position); % Equation (3.5)-part 2
        X2=Beta_pos-A2*D_beta; % Equation (3.6)-part 2
        
        r1=rand();
        r2=rand();
        
        A3=2*a*r1-a; % Equation (3.3)
        C3=2*r2; % Equation (3.4)
        
        D_delta=abs(C3*Delta_pos-Agents(i).Position); % Equation (3.5)-part 3
        X3=Delta_pos-A3*D_delta; % Equation (3.5)-part 3
        
        Agents(i).Position=(X1+X2+X3)/3;% Equation (3.7)
        
        % Calculate objective function for each search agent
        Agents(i).Position = max(Agents(i).Position,lb);
        Agents(i).Position = min(Agents(i).Position,ub);
        Agents(i).fitness=fobj(Agents(i).Position);
        FE=FE+1;