基础-最短路

最新推荐文章于 2024-05-21 10:33:53 发布

有暇即扫地

最新推荐文章于 2024-05-21 10:33:53 发布

阅读量120

点赞数

文章标签： c++ 算法开发语言

本文链接：https://blog.csdn.net/weixin_61600873/article/details/127016706

版权

引入

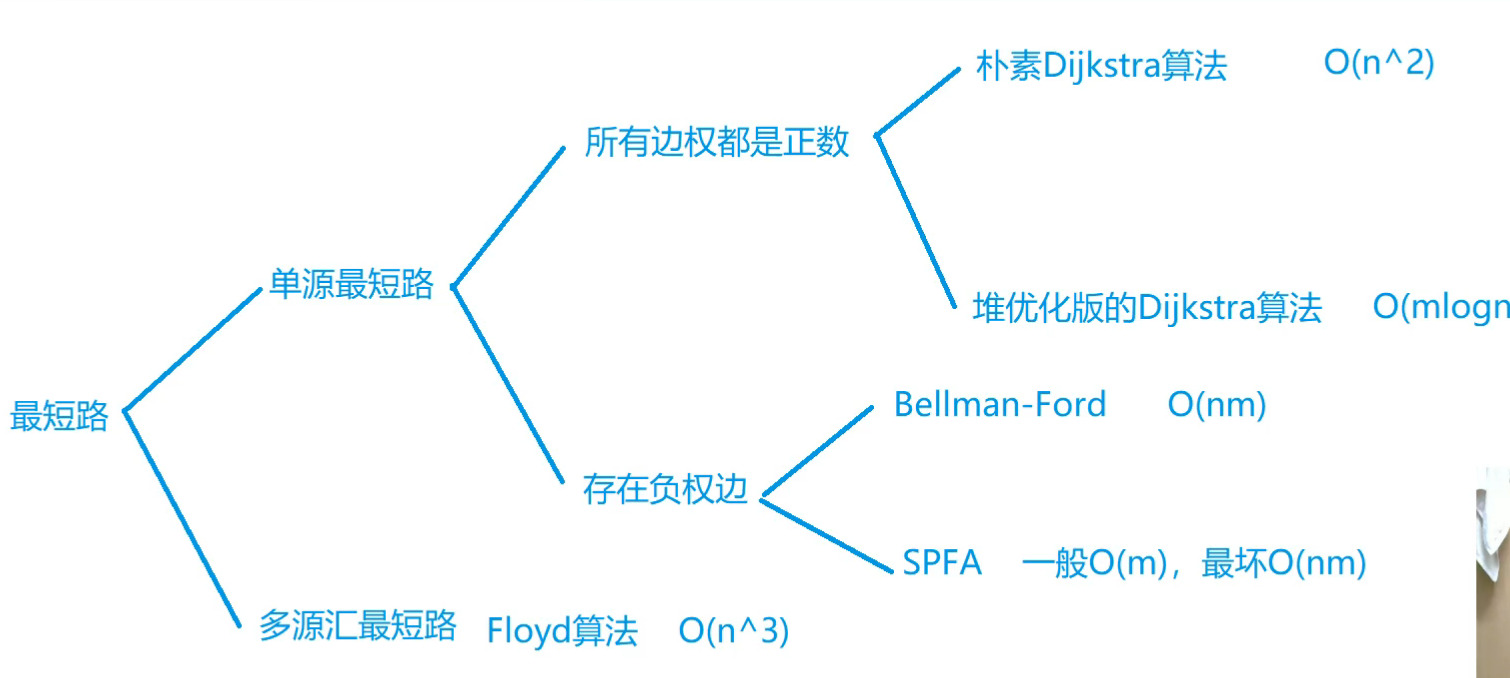
分类

最短路问题包括单源最短路和多源汇最短路

稠密图（边是n^2级别）则优选朴素Dijkstra,否则选堆优化版；

虽然SPFA比BellmanFord性能优，但适用范围更局限；

难点

在于建图，将问题转换成模型、抽象成最短路问题，而不是算法原理；在学习时应该侧重于实现，而不是原理。

朴素Dijkstra n^2

算法步骤

当前已经确定了最短距离的点放在集合s中

初始化dist[1]=0, dist[i]=+∞；
for i in(0,n):
1. t=找到不在s中的、距离最近的点
2. t加入到s
3. 用t更新其它点的距离

时间复杂度n^2

存储

稠密图用邻接矩阵，稀疏图用邻接表；

代码

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N=510;

int g[N][N];    //为稠密阵所以用邻接矩阵存储
int dist[N];    //用于记录每一个点距离第一个点的距离
bool st[N];     //用于记录该点的最短距离是否已经确定

int n,m;

int Dijkstra()
{
    memset(dist, 0x3f,sizeof dist);     //初始化距离  0x3f代表无限大

    dist[1]=0;  //第一个点到自身的距离为0

    for(int i=0;i<n;i++)      //有n个点所以要进行n次 迭代
    {
        int t=-1;       //t存储当前访问的点

        for(int j=1;j<=n;j++)   //这里的j代表的是从1号点开始
            if(!st[j]&&(t==-1||dist[t]>dist[j]))     
                t=j;

        st[t]=true;   

        for(int j=1;j<=n;j++)           //依次更新每个点所到相邻的点路径值
            dist[j]=min(dist[j],dist[t]+g[t][j]);
    }

    if(dist[n]==0x3f3f3f3f) return -1;  //如果第n个点路径为无穷大即不存在最低路径
    return dist[n];
}
int main()
{
    cin>>n>>m;

    memset(g,0x3f,sizeof g);    //初始化图 因为是求最短路径
                                //所以每个点初始为无限大

    while(m--)
    {
        int x,y,z;
        cin>>x>>y>>z;
        g[x][y]=min(g[x][y],z);     //如果发生重边的情况则保留最短的一条边
    }

    cout<<Dijkstra()<<endl;
    return 0;
}

堆优化Dijkstra mlogn

引入

优化查找最近的点n^2->n，但是堆修改变为m->mlogn;

算法步骤

当前已经确定了最短距离的点放在集合s中

初始化dist[1]=0, dist[i]=+∞；
堆维护最小距离点，稀疏图用邻接表存
1. t=找到不在s中的、距离最近的点
2. 过滤冗余元素，t加入到s
3. 用t更新其它点的距离，入堆

代码

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>//堆的头文件

using namespace std;

typedef pair<int, int> PII;//堆里存储距离和节点编号

const int N = 1e6 + 10;

int n, m;//节点数量和边数
int h[N], w[N], e[N], ne[N], idx;//邻接矩阵存储图
int dist[N];//存储距离
bool st[N];//存储状态

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);//距离初始化为无穷大
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;//小根堆
    heap.push({0, 1});//插入距离和节点编号

    while (heap.size())
    {
        auto t = heap.top();//取距离源点最近的点
        heap.pop();

        int ver = t.second, distance = t.first;//ver:节点编号，distance:源点距离ver 的距离

        if (st[ver]) continue;//如果距离已经确定，则跳过该点
        st[ver] = true;

        for (int i = h[ver]; i != -1; i = ne[i])//更新ver所指向的节点距离
        {
            int j = e[i];
            if (dist[j] > dist[ver] + w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j});//距离变小，则入堆,
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);
    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    cout << dijkstra() << endl;

    return 0;
}

Bellman-Ford算法 nm

算法流程

for n循环n次
- 备份dist，每次循环只用上一次的dist，防止串联，保证k次的限制
- for each edge(a,b,w)遍历所有边
  - distance[b]=min(dist[b],dist[a]+w);更新距离

循环n次有三角不等式dist[b]<=dist[a]+w,n次循环叫做松弛操作；

有负权存在（回路），最短路不一定存在；

迭代k次，dist是从1号点，经过不超过k条边的最短距离；则迭代n次是全局最短路径；

#include<iostream>
#include<cstring>

using namespace std;

const int N = 510, M = 10010;

struct Edge {
    int a;
    int b;
    int w;
} e[M];//把每个边保存下来即可
int dist[N];
int back[N];//备份数组防止串联
int n, m, k;//k代表最短路径最多包涵k条边

int bellman_ford() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for (int i = 0; i < k; i++) {//k次循环
        memcpy(back, dist, sizeof dist);
        for (int j = 0; j < m; j++) {//遍历所有边
            int a = e[j].a, b = e[j].b, w = e[j].w;
            dist[b] = min(dist[b], back[a] + w);
            //使用backup:避免给a更新后立马更新b, 这样b一次性最短路径就多了两条边出来
        }
    }
    if (dist[n] > 0x3f3f3f3f / 2) return -1;
    else return dist[n];

}

int main() {
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 0; i < m; i++) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        e[i] = {a, b, w};
    }
    int res = bellman_ford();
    if (res == -1) puts("impossible");
    else cout << res;

    return 0;
}

SPFA m~mn

可以看作是Bellman-Ford的改进，即每次迭代不一定会更新dist；

只有我变小了，我的后继才能变小；

算法流程

queue<- 1;队列村的是所有待更新的点

while 队列不空

取队头，弹出队头

更新队头的所有出边；

判断负环

新建数组cnt，每更新一次队列就计数，最后判定cnt>=n则存在负环（抽屉原理）；

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 100010;

int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N],cnt[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

bool spfa()
{

    queue<int> q;
     for (int i=1;i<=n;i++){
            st[i]=true;
            q.push(i);}
    while (q.size())
    {
       
        
        int t = q.front();
        q.pop();

        st[t] = false;

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                cnt[j]=cnt[t]+1;
                if (cnt[j]>=n) return true;
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    return false;
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);

    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    bool t = spfa();

    if (spfa()) cout<<"Yes"<<endl;
    else cout<<"No\n";
    return 0;
}

Floyd

算法步骤

k:1-n
i:1-n
j:1-n
d[i,j]=min(d[i,j],d[i,k]+d[k,j]);

#include <iostream>
using namespace std;

const int N = 210, M = 2e+10, INF = 1e9;

int n, m, k, x, y, z;
int d[N][N];

void floyd() {
    for(int k = 1; k <= n; k++)
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main() {
    cin >> n >> m >> k;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            if(i == j) d[i][j] = 0;
            else d[i][j] = INF;
    while(m--) {
        cin >> x >> y >> z;
        d[x][y] = min(d[x][y], z);
        //注意保存最小的边
    }
    floyd();
    while(k--) {
        cin >> x >> y;
        if(d[x][y] > INF/2) puts("impossible");
        //由于有负权边存在所以约大过INF/2也很合理
        else cout << d[x][y] << endl;
    }
    return 0;
}

有暇即扫地

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
基础-最短路

在于建图，将问题转换成模型、抽象成最短路问题，而不是算法原理；迭代k次，dist是从1号点，经过不超过k条边的最短距离；新建数组cnt，每更新一次队列就计数，最后判定cnt>=n则存在负环（抽屉原理）；循环n次有三角不等式dist[b]n，但是堆修改变为m->mlogn;有负权存在（回路），最短路不一定存在；更新队头的所有出边；只有我变小了，我的后继才能变小；
复制链接

扫一扫