目录
数字游戏I
S.Digitsum AtcoderEducational dpcontest
决策树解决数位dp问题的局限性:如果需要维护参数过大,很有可能爆空间。
SP3928 MDIGITS - Counting Digits 洛谷
特点: 求某个区间 内部具有某种性质的数的个数,通常利用前缀和转化成从1---n中具有某种性质的个数 利用公式
求出答案。
思路:通尝使用决策树的思想解决问题。
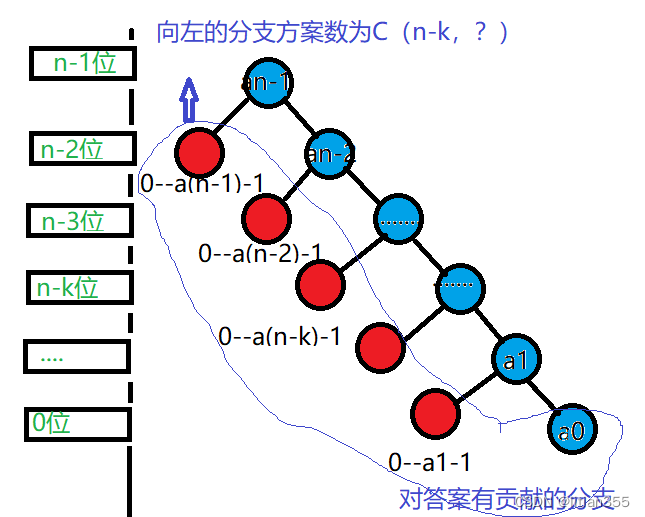
可以看出答案是由所有左边分支中满足条件数的个数和右边满足要求一条链的方案数之和。
具体求解思路就是用dp思想直接求出左边每个分支的具体方案数量,累加后加上一些特判
学习心得:数位dp问题经常和组合数结合在一起,如果能够找出规律,利用组合数能很快求出答案。否则的话就考虑定义状态进行状态转移,状态定义一般就是最高位是j的所有i位数中满足条件的所有数。
利用决策树的好处,能够锻炼自己动态规划状态的表示与转移,解题思路也会更加清晰。
例题:
度的数量 Acwing1081
求给定区[L,R]上所有满足在B进K位为1,其余为都为0的数的个数。
数位dp的优化,数位和可以利用取模优化空间,例如数位和是k的倍数等价于modk==0;
数位乘积可以用lcm优化。
求给定区间 [X,Y]中满足下列条件的整数个数:这个数恰好等于 K个互不相等的 B 的整数次幂之和。
输入格式
第一行包含两个整数 X 和 Y,接下来两行包含整数 K和 B。
输出格式
只包含一个整数,表示满足条件的数的个数。
数据范围
1≤X≤Y≤2^31-1
1≤K≤20
2≤B≤10
输入样例:
15 20
2
2
输出样例:
3
用last表示前面已经填了last个1,res表示的是答案,画出相应的树形结构,左边分支的合法方案数恰好就是C(i,k-last)。
#include<bits/stdc++.h>
using namespace std ;
#define int long long
const int N=36;
int f[N][N];
int l,r,k,b;
void init(){
for(int i=0;i<N;i++){
for(int j=0;j<=i;j++){
if(!j||!i) f[i][j]=1;
else f[i][j]=f[i-1][j-1]+f[i-1][j];
}
}
}
int dp(int x){
if(!x) return 0;
vector<int>nums;
int res=0,last=0;
while(x) nums.push_back(x%b),x/=b;//转换成b进制
for(int i=nums.size()-1;i>=0;i--){ 枚举第i位
int tem=nums[i];
if(tem){//如果第i位为0直接跳过
if(k-last>=0)res+=f[i][k-last];//第i位填0;
if(tem>1)//如果说第i位大于1,那么第i位只能填1,剩余方案数就是f[i][k-last-1],直接退
//出循环。
{
if(k-last-1>=0)
res+=f[i][k-last-1];
break;
}else if(tem==1){
last++;
if(last>k) break;//为什么;//last==k是要特判,不能提前退出
}
}
if(i==0&&k==last ) res++;
}
return res;
}
signed main(){
cin>>l>>r>>k>>b;
init();
cout<<dp(r)-dp(l-1)<<endl;
return 0;
}科协里最近很流行数字游戏。
某人命名了一种不降数,这种数字必须满足从左到右各位数字呈非下降关系,如 123,446。
现在大家决定玩一个游戏,指定一个整数闭区间 [a,b],问这个区间内有多少个不降数。
输入格式
输入包含多组测试数据。
每组数据占一行,包含两个整数 a 和 b。
输出格式
每行给出一组测试数据的答案,即 [a,b] 之间有多少不降数。
数据范围
1≤a≤b≤2^31−1
输入样例:
1 9
1 19
输出样例:
9
18定义 f[i][j]表示最高位是j的,总位数为i的所有不降数的个数。‘
last表示上以为填的数。
根据树形图
左边分支所有方案就是所有以【last,x-1】之间某一个数为最高位,总位数为i+1,的所有不降数的个数,如果last>x,之后答案不会再增加直接break就行,最后特判i==0。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=16;
LL L,R;
LL f[N][N];
void init(){
// f[i][j]表示最高位是j的,总位数为i的所有不降数的个数。
for(int i=0;i<=9;i++) f[1][i]=1;
for(int i=2;i<=N;i++){
for(int j=0;j<=9;j++){
for(int k=j;k<=9;k++){
f[i][j]+=f[i-1][k];
}
}
}
}
LL dp(LL n){
if(!n) return 1;
int res=0;
int last=0;
vector<int >nums;
while(n) nums.push_back(n%10),n/=10;
for(int i=nums.size()-1;i>=0;i--){
int x=nums[i];
for(int j=last;j<x;j++){
res+=f[i+1][j];
}
if(last>x) break;//当前位一定要比上一位大,否则就退出循环。
if(!i) res++;
last=x;
}
return res;
}
signed main(){
init();
while(cin>>L>>R){
cout<<dp(R)-dp(L-1)<<endl;
}
return 0;
}windy数
Windy 定义了一种 Windy 数:不含前导零且相邻两个数字之差至少为 2 的正整数被称为 Windy 数。
Windy 想知道,在 A和 B 之间,包括 A 和 B,总共有多少个 Windy 数?
输入格式
共一行,包含两个整数 A和 B。
输出格式
输出一个整数,表示答案。
数据范围
1≤A≤B≤2×1e9
输入样例1:
1 10
输出样例1:
9
输入样例2:
25 50
输出样例2:
20思路:和上一题思路类似,定义f[i][j]为有i位数最高位为j的所有windy数的个数,last表示上一次填的数字。
本题要求不含前导零,我们可以先处理所有不含有前导零的数,最后特判含有前导零的windy数。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL A,B;
const int N=16;
LL f[N][N];
void init(){
for(int i=0;i<=9;i++) f[1][i]=1;
for(int i=2;i<=N;i++){
for(int j=0;j<=9;j++){
for(int k=0;k<=9;k++){
if(abs(j-k)>1)f[i][j]+=f[i-1][k];
}
}
}
}
LL dp(LL n){
if(!n) return 0;
LL res=0,last=-2;
vector<int>nums;
while(n) nums.push_back(n%10),n/=10;
for(int i=nums.size()-1;i>=0;i--){
int x=nums[i];
for(int j=i==nums.size()-1;j<x;j++){
if(abs(j-last)>1) res+=f[i+1][j];
}
if(abs(last-x)>1)last=x;
else break;
if(!i) res++;
}
//特殊处理有前导0的情况
for(int i=1;i<=nums.size()-1;i++){
for(int j=1;j<=9;j++){
res+=f[i][j];
}
}
return res;
}
signed main(){
init();
cin>>A>>B;
cout<<dp(B)-dp(A-1)<<endl;
return 0;
}
由于科协里最近真的很流行数字游戏。
某人又命名了一种取模数,这种数字必须满足各位数字之和 mod N为 0。
现在大家又要玩游戏了,指定一个整数闭区间 [a.b],问这个区间内有多少个取模数。
输入格式
输入包含多组测试数据,每组数据占一行。
每组数据包含三个整数 a,b,N。
输出格式
对于每个测试数据输出一行结果,表示区间内各位数字和 mod N为 0 的数的个数。
数据范围
1≤a,b≤2^31−1
1≤N<100
输入样例:
1 19 9
输出样例:
2思路:先画出决策树,左侧分支相当与固定前size()-i-1位,设last表示已经确定好的数位之和,由于 .dp求出左侧分支方案数;
设 表示i位数最高位是j的位数和modP为k的所有数的个数。
公式:
、
最后特判n是否满足要求。
code:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL a,b,base;
const LL N=110;
LL f[17][11][N];//最高位是j的i位数满足中数位和mod base等于k的数的个数
LL mod(LL x,LL base) {
return (x%base+base)%base;
}
void init(LL base){
memset(f,0,sizeof f);
for(LL i=0;i<=9;i++)f[1][i][i%base]++;
for(int i=2;i<=15;i++)
{
// cout<<"ac"<<endl;
for(int j=0;j<=9;j++){
for(int k=0;k<base;k++)
for(int t=0;t<=9;t++){
f[i][j][k]+=f[i-1][t][mod(k-j,base)];
}
}
}
}
LL dp(LL n,LL base){
if(!n) return 1;
LL res=0,last=0;
vector<int >nums;
while(n) nums.push_back(n%10),n/=10;
for(int i=nums.size()-1;i>=0;i--){
LL x=nums[i];
for(int j=0;j<x;j++){
res+=f[i+1][j][mod(-last,base)];
}
last+=x;
if(!i&&last%base==0) res++;
}
return res;
}
signed main(){
while(cin>>a>>b>>base){
init(base);
cout<<dp(b,base)-dp(a-1,base)<<endl;
}
return 0;
}不要62
杭州人称那些傻乎乎粘嗒嗒的人为 62(音:laoer)。
杭州交通管理局经常会扩充一些的士车牌照,新近出来一个好消息,以后上牌照,不再含有不吉利的数字了,这样一来,就可以消除个别的士司机和乘客的心理障碍,更安全地服务大众。
不吉利的数字为所有含有 4或 62 的号码。例如:62315,73418,88914 都属于不吉利号码。但是,61152虽然含有 6和 2,但不是 连号,所以不属于不吉利数字之列。
你的任务是,对于每次给出的一个牌照号区间 [n,m],推断出交管局今后又要实际上给多少辆新的士车上牌照了。
输入格式
输入包含多组测试数据,每组数据占一行。
每组数据包含一个整数对 n 和 m。
当输入一行为“0 0”时,表示输入结束。
输出格式
对于每个整数对,输出一个不含有不吉利数字的统计个数,该数值占一行位置。
数据范围
1≤n≤m≤1e9
输入样例:
1 100
0 0
输出样例:
80思路:题目要求的幸运数就是数位里不含4和62的数的个数,设表示最高位是j的i位数中所有幸运数的个数,预处理公式:
当j==4时可以直接跳过。
设last表示上次选取的数,当前数字已经不是幸运数时跳出循环。
code:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL l,r;
const LL N=12;
LL f[N][N];//f[i][j]表示的是最高位是j的i位数中幸运数的个数。
void init(){
for(int i=0;i<=9;i++) if(i!=4) f[1][i]++;
for(int i=2;i<=N;i++){
for(int j=0;j<=9;j++){
if(j==4) continue;
for(int k=0;k<=9;k++){
if(k==4||j==6&&k==2) continue;
f[i][j]+=f[i-1][k];
}
}
}
}
LL dp(LL n){
if(!n) return 1;
LL res=0,last=0;
vector<int >nums;
while(n) nums.push_back(n%10),n/=10;
for(int i=nums.size()-1;i>=0;i--){
LL x=nums[i];
for(int j=0;j<x;j++){
if(j==4||last==6&&j==2) continue;
res+=f[i+1][j];
}
if(x==4||last==6&&x==2) break;
last=x;
if(!i)res++;
}
return res;
}
signed main(){
init();
while(cin>>l>>r,l||r){
cout<<dp(r)-dp(l-1)<<endl;
}
return 0;
}C. Classy Numbers cf1036C
让我们称某个正整数为classy,如果它的十进制表示包含不超过3个非零位。例如,数字4、200000、10203是classy 的,而数字4231、102306、7277420000则不是。
给定一个线段[L,R]。计算L≤x≤R的calssy数x的数量。
每个测试用例包含几个片段,对于每一个片段,您都需要分别解决问题。
输入
第一行包含一个整数T(1≤T≤1e4)——一个测试用例中的段数。
接下来的T行包含两个整数Li和Ri(1≤Li≤Ri≤1e18)。
输出
打印T行——第i行应该包含一个段[Li,Ri]上的经典整数的数量。
思路:
classy数的特点是不含超过三个非零位,考虑每一位是非零位还是零位,利用决策树,用组合数学的知识转移即可。
如果第i+1位是x,设last表示已经填了last个非0数,考虑第i+1位填的是0还是那x-1 个非0,得到
code:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL tt;
LL l,r;
const LL N=20;
LL f[N][N];
void init(){
for(int i=0;i<N;i++){
for(int j=0;j<=i;j++){
if(!i||!j) f[i][j]=1;
else f[i][j]=f[i-1][j]+f[i-1][j-1];
}
}
}
LL dp(LL n){
if(!n) return 1;
vector<int >nums;
LL res=0,last=0;
while(n) nums.push_back(n%10),n/=10;
for(int i=nums.size()-1;i>=0;i--){
int x=nums[i];
if(x){
int p=1;
for(int k=0;k<=3-last;k++,p*=9) {
res+=f[i][k]*p;
}
p=1;
for(int k=0;k<=2-last;k++,p*=9) res+=(x-1)*f[i][k]*p;
last++;
}
if(last>3) break;
if(!i&&last<=3) res++;
}
return res;
}
signed main(){
cin>>tt;
init();
while(tt--){
cin>>l>>r;
cout<<dp(r)-dp(l-1)<<endl;
}
return 0;
}
// 4
// 1 1000
// 1024 1024
// 65536 65536
// 999999 1000001
// 1000
// 1
// 0
// 2
S.Digitsum AtcoderEducational dpcontest
Problem Statement
Find the number of integers between 1 and K (inclusive) satisfying the following condition, modulo 109+7:
- The sum of the digits in base ten is a multiple of D.
Constraints
- All values in input are integers.
思路: 考虑到k是一个很大的数,k的数位和相应也会很大,但不会超过1e5,但D是一个非常小的数,设一个数n的数位和是sum , sum是d 的倍数当且仅当n满足以下条件:
1.n不含前导零。
2.n的数位和sum%d==0;
注意:如果直接将状态定义为最高位是j的所有i位数中,数位和是k的数的个数一定会爆空间,而d非常小我们可以这样定义:
状态 表示最高位是j的所有i位数中,数位和sum是k的倍数的数的个数(sum%k==0)。
由于d<100,空间最多是 1e4*d*10=1e7,恰到好处。
接下来更新状态:
最后利用决策树更新状态即可。
code:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e4+10;
const LL P=1e9+7;
string n;
LL d;
LL mod(LL x){
return (x%d+d)%d;
}
LL f[N][10][103];
void init(){
for(int i=0;i<10;i++) {
f[1][i][mod(i)]++;
}
for(int i=2;i<N;i++){
for(int j=0;j<=9;j++){
for(int k=0;k<=d;k++){
for(int t=0;t<=9;t++){
f[i][j][k]=(f[i][j][k]+f[i-1][t][mod(k-j)])%P;
}
}
}
}
}
LL dp(string nums){
LL res=0,last=0;
reverse(nums.begin(),nums.end());
for(int i=nums.size()-1;i>=0;i--){
int x=nums[i]-'0';
for(int j=i==nums.size()-1;j<x;j++){
res=(res+f[i+1][j][mod(-last)])%P;
}
last+=x;
if(!i&&last%d==0) res++;
}
for(int i=1;i<=nums.size()-1;i++){
for(int j=1;j<=9;j++) res=(res+f[i][j][0])%P;
}
return res;
}
signed main(){
cin>>n>>d;
init();
cout<<dp(n)<<endl;
return 0;
}[ZJOI2010] 数字计数 洛谷
设dp[i][j][k]表示一个长度为ii的数,其中最高位是j,k这个数码一共出现的次数
之后转移的话,我们需要枚举当前位数,当前最高位填什么数,次高位填什么数,之后转移一下就好了
显然有
但是这就完了吗,显然不是啊
我们填上的最高位可是出现了很多次,但是一次都没有被记录进去
那也好办,我们让剩下的i-1为随意选择只考虑当前最高位上出现的数就好了(因为那些随意选择的数码已经被计入答案了)
于是根据乘法原理,还有
之后就是数位dp的板子了
代码
#include<iostream>
#include<cstring>
#include<cstdio>
#define re register
#define maxn 14
#define LL long long
LL dp[maxn][10][10];
LL L,R;
LL ans[10][2];
int a[maxn],num;
inline LL quick(LL a,LL b)
{
LL s=1;
while(b)
{
if(b&1) s*=a;
b>>=1;
a*=a;
}
return s;
}
inline void slove(LL x,int pd)
{
memset(dp,0,sizeof(dp));
num=0;
memset(a,0,sizeof(a));
while(x)
{
a[++num]=x%10;
x/=10;
}//分解数位
for(re int i=0;i<=9;i++) dp[1][i][i]=1;//初始化
for(re int i=2;i<=num;i++)//枚举位数
for(re int j=0;j<=9;j++)//当前最高位
{
for(re int k=0;k<=9;k++)//次高位
{
for(re int p=0;p<=9;p++)
dp[i][j][p]+=dp[i-1][k][p];
}
dp[i][j][j]+=quick(10,i-1);//乘法原理
}
for(re int i=1;i<num;i++)//位数比x小的,一定能够满足条件
for(re int j=1;j<=9;j++)//不能有前导零
for(re int k=0;k<=9;k++)
ans[k][pd]+=dp[i][j][k];
for(re int i=1;i<a[num];i++)//位数相同,但最高位比x小
for(re int k=0;k<=9;k++)
ans[k][pd]+=dp[num][i][k];
for(re int i=num-1;i>=1;i--)//当前不同的那一位,[i+1,num]与x完全相同
{
for(re int j=0;j<a[i];j++)//不同的这一位也必须必对应x位置上的数小
{
for(re int k=0;k<=9;k++)
ans[k][pd]+=dp[i][j][k];
}
for(re int p=num;p>i;p--)
ans[a[p]][pd]+=a[i]*quick(10,i-1);
//由于我们保证[i+1,num]相同,那么这些数码也应该计入答案,于是还是一个乘法原理
}
//但是这个dp全程都不能处理出x是否满足条件
//因为最后也只是判断第一位上的数比给定数的第一位小
//所以slove(x)其实求得是[0,x)满足条件的数的个数
}
int main()
{
scanf("%lld%lld",&L,&R);
slove(R+1,0),slove(L,1);
for(re int i=0;i<=9;i++)
printf("%lld ",ans[i][0]-ans[i][1]);
putchar(10);
return 0;
}决策树解决数位dp问题的局限性:如果需要维护参数过大,很有可能爆空间。
这个时候用dfs求解更好。
P6218 Round Numbers S 洛谷
令 为满足由 i 位组成,且其中有 j个1,第 i 位(从右往左数)为 k 的二进制数的数量。
可以得出状态转移方程:
边界:
令f(x) 为区间 [1,x-1] 内的“圆数”个数,则区间 [L,R]内的“圆数”个数为 f(R+1)−f(L)。
对于求f(x),我们先将 x 转换成二进制,设其二进制位数为 len。
-
将二进制位数小于 len 的“圆数”个数统计到答案中。
-
对于 x 的二进制除首位外的每一位 i,都判断其是否为1 。如果为1,说明存在一些数,它们小于 x,且二进制表示中的前 i−1 位与x 相同,第 i 位为0 。然后将这些数中的“圆数”个数加入答案即可。
#include <cstdio>
#include <cstring>
using namespace std;
#define in __inline__
typedef long long ll;
#define rei register int
#define FOR(i, l, r) for(rei i = l; i <= r; ++i)
#define FOL(i, r, l) for(rei i = r; i >= l; --i)
char inputbuf[1 << 23], *p1 = inputbuf, *p2 = inputbuf;
#define getchar() (p1 == p2 && (p2 = (p1 = inputbuf) + fread(inputbuf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
in int read() {
int res = 0; char ch = getchar(); bool f = true;
for(; ch < '0' || ch > '9'; ch = getchar())
if(ch == '-') f = false;
for(; ch >= '0' && ch <= '9'; ch = getchar())
res = res * 10 + (ch ^ 48);
return f ? res : -res;
}
const int N = 40;
ll dp[N][N][2];
int a, b, A[N], la, lb, B[N];
ll solve(int x[], int len) {
ll res = 0; int s0 = 0, s1 = 1;
//s0表示0的个数,s1表示1的个数
FOL(i, len - 1, 1) FOR(j, 0, (i >> 1)) res += dp[i][j][1];//第1类数
FOL(i, len - 1, 1) {//第二类数
if(x[i]) FOR(j, 0, i) if(s0 + i - j >= s1 + j) res += dp[i][j][0];
x[i] ? (++s1) : (++s0);
}
return res;
}
signed main() {
a = read(), b = read();
for(; a; a >>= 1) A[++la] = a & 1;
for(; b; b >>= 1) B[++lb] = b & 1;//转换成二进制
++B[1];
for(rei i = 2; i <= lb && B[i - 1] == 2; ++i) B[i - 1] = 0, ++B[i];
if(B[lb] == 2) B[lb] = 0, B[++lb] = 1;
while(!A[la]) --la;
while(!B[lb]) --lb;//给B加上1
dp[1][0][0] = dp[1][1][1] = 1;
FOR(i, 2, lb) FOR(j, 0, i) {//DP
if(j < i) dp[i][j][0] = dp[i - 1][j][1] + dp[i - 1][j][0];
if(j) dp[i][j][1] = dp[i - 1][j - 1][0] + dp[i - 1][j - 1][1];
}
printf("%lld\n", solve(B, lb) - solve(A, la));
return 0;//结束
}SP3928 MDIGITS - Counting Digits 洛谷
一道经典的数位 DP,这里用记忆化搜索实现。
f(i,j) 表示当前位数为 i,当前数码个数为 j 时的状态。
从高到低枚举每一位,考虑每一位都可以填哪些数字。
如果当前位正好是要查询的数码,sum 就加一。
还要考虑有前导零的情况,所以要加上一个判断前导零的参数 leadlead。如果有前导零,且当前数码正好为 0,sum 不变,然后接着扫下去。即 sum+(((!lead)||i)&&(i==digit))。
剩下的就是套数位 DP 的模板了:
AC code:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long a[20],f[20][20000],l,r;
long long dfs(int pos,int digit,long long sum,bool lead,bool limit){
//pos:当前数位; digit:要找的数码; sum:要找的数码的总和; lead:判断前导零; limit:判断限制位
if(pos==0) return sum;
if(!limit&&!lead&&f[pos][sum]!=-1) return f[pos][sum];
int up=limit?a[pos]:9;
long long ans=0;
for(int i=0;i<=up;i++)
ans+=dfs(pos-1,digit,sum+(((!lead)||i)&&(i==digit)),lead&&!i,limit&&(i==up));
if(!limit&&!lead) f[pos][sum]=ans;
return ans;
}
long long handle(long long num,int digit){
int pos=0;
while(num)
a[++pos]=num%10,num/=10;
return dfs(pos,digit,0,1,1);
}
signed main(){
memset(f,-1,sizeof(f));
while(scanf("%lld %lld",&l,&r)==2&&l&&r){
if(r<l) swap(l,r); //注意:r有可能小于l
for(int i=0;i<=9;i++)
cout<<handle(r,i)-handle(l-1,i)<<" ";
puts("");
}
return 0;
} CF55D Beautiful numbers
先说在前面,因为数据量极大,所以一个个的枚举是不行的!!! 所以我们可以将[l,r]的区间变成[1,r]-[1,l-1],这就是所谓的差分。
为了解决这道题,我们还需要了解两点小学数学知识:
1.一个数如果可以被几个数整除,那么这个数也可以被那几个数的最小公倍数整除;
2."1,2,3,4,5,6,7,8,9"的最小公倍数为2520 (废话) 。
知道后我们就可以开始解题了。
首先,因为是DP,所以我们需要一个DP数组来将宝贵中间的运算结果储存下来,之后可以直接使用(因为DP使用的是DFS,所以也可以看作记忆化剪枝)。
接着,因为是数位DP,所以我们需要DP数组开一个维度来储存当前位数。
其次,因为最后要检测这个数是否满足条件: 能被它自己的每一位数上的数整除 (也就是被每一位上的数的最小公倍数整除),所以我们又需要开两个维度:一个存数的值,一个存这个数每一位上的数的最小公倍数。
但我们不难发现,想存9*10(18)是不可能的,又因为题目最后是检测这个数能否被每一位上的数的最小公倍数整除,假设这个数为A,那么A与(A%2520)其实是等效的,所以我们可以不存A而存(A%2520),这样问题就解决了
于是我们就开了一个数组:DP[20(因为总共就19位数)][2521][2521](DP数组内的数据表示满足当前情况的 Beautiful numbers 的个数),准备直接开始跑,然后就可以坐等AC内存超限了。
所以问题又来了:数组开不下。于是我们思考怎么减小数组:第一二位已经到最小了,只能改第三维。我们通过计算发现,1~2520中,2520的因数只有48个,也就是满足条件的情况只有48种,所以第三维大小直接变为48(这到底是属于撞鸭还是离散化?蒟蒻傻傻分不清)
上代码(还有些细节部分会在代码中注释)
!!!因为借鉴了题解dalao们的思路,所以代码会很相像!!!
#define Tokisaki return //狂三我老婆!!!
#define Kurumi 0; //狂三赛高!!!
#include <cstdio>
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#define rint register int //加速用的,直接用int也可以
typedef long long ll;
using namespace std;
const int MOD=2520;
int t,book[MOD+1];
vector <int> shu;
ll l,r,dp[25][MOD+1][50]; //特别注意:DP数组一定要开long long类型,不然会炸
inline int gcd (int x,int y) //gcd函数,虽然STL里面自带(为__gcd),但还是自己手写了一个
{
if(x>y) swap(x,y);
if(y%x==0) return x;
return gcd(x,y%x);
}
inline int _lcm (int x,int y) //lcm函数,求最小公约数
{
return x*y/gcd(x,y);
}
inline void init() //初始化用的函数
{
memset(dp,-1,sizeof(dp)); //将DP数组初始化
rint num=0;
for(rint i=1;i<=MOD;i++) //离散化,将2520的因数们从1开始标记
{
if(MOD%i==0)
{
num++;
book[i]=num;
}
}
}
ll dfs(int pos,int he,int lcm,int sp) //数位DP主要内容
//pos:当前处理到第几位;
//he:pos位之前的数%2520;
//lcm:pos位之前的数的每一位数的最小公倍数;
//sp:特判当前是否为范围内的最大值
{
if(pos==-1) return he%lcm==0; //如果处理完了最后一位,数如果满足条件,返回1,否则返回0
if(sp==0&&dp[pos][he][book[lcm]]!=-1) return dp[pos][he][book[lcm]]; //如果不是最大值的情况,并且当前情况以处理过,直接返回值
ll ans=0;
int MAX=sp==1?shu[pos]:9; //如果前几位是最大值情况,那么当前位最大值为这一位的数,否则为9
for(rint i=0;i<=MAX;i++) //从0枚举
{
int next_he=(he*10+i)%MOD; //计算包含当前位时数的值
int next_lcm=lcm;
if(i)
{
next_lcm=_lcm(next_lcm,i);//计算包含当前位时所有位上的数的最小公倍数(当前位所选数不为0,如果为零就是原数)
}
ans+=dfs(pos-1,next_he,next_lcm,sp&&i==MAX); //向下搜索,如果前几位是最大值情况,并且当前位为最大值时,sp=1
}
if(sp==0) //如果不是最大值情况,记录运算结果
{
dp[pos][he][book[lcm]]=ans;
}
return ans;
}
inline ll work (ll num) //处理数据加求值函数
{
shu.clear(); //一定要记得清空
while(num) //将数值按为存入
{
shu.push_back(num%10);
num/=10;
}
return dfs(shu.size()-1,0,1,1); //从最高位开始搜索
}
int main ()
{
init(); //初始化
cin>>t;
for(int i=1;i<=t;i++)
{
cin>>l>>r;
cout<<work(r)-work(l-1)<<endl;
}
Tokisaki Kurumi //狂三我老婆,不服憋着
}






















 2854
2854











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










