相信大家都已经了解了欧拉函数的定义
在1~N当中,与N互质的数的个数被叫做欧拉函数,简写成Φ(N);
在算数基本定理中我们可以把一个数N分解成所有质因子的乘积的形式,记作
N = p1^a1 * p2^a2 *.... *pn^an;
所以欧拉函数的计算公式
在敲代码的时候常常不是以上面的形式写,而是这种
Φ(x)=x * (p1 - 1)/p1 * (p2 - 1)/p2 * ..... * (pn - 1)/pn;
这种写法的好处是不会因为出现浮点数存储误差导致的计算结果的错误。
关于欧拉函数的证明


证毕
附加代码模板(y总的代码果然很优雅)可以封装成一个函数,简洁大方,比较好debug
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int main()
{
int n;
scanf("%d",&n);
while(n--)
{
int x;
scanf("%d",&x);
LL res=x;
for(int i=2;i<=x/i;i++)
{
if(x%i==0)
{
res=res*(i-1)/i;
while(x%i==0) x/=i;
}
}
if(x>1) res=res*(x-1)/x;
printf("%lld\n",res);
}
return 0;
}因此延伸出一个非常牛逼的公式(欧拉公式)orz大佬
若a,n互质,则有a^Φ(n)≡1(mod n)
证明
1.因为有Φ(n),所以首先找出1~n中所有与n互质的数,x1,x2...xn;
2.令p1=a*x1,p2=a*x2,p3=a*x3...pn=a*xn。证明所有的p在(mod n)的情况下,两两不相等
采用反证法,若pi ≡ pj (mod n) 则会有 pi - pj = k * n(k为任意常数) ,a( xi - xj ) = k * n
又因为a,n互质,即a中没有没有与n相同的质因子,所以xi - xj 一定是 n的倍数,但是 xi,xj都比n小,且与n互质,不可能是n的倍数,所以产生矛盾。所以任意两个pi,pj在mod n的情况下都不会相等,同时,xi,xj在mod n的情况下也不可能相等。
这里可以提供一种思路 若任意的x1,x2, 假设x2>x1, x1%n = k, x2%n = k, 则x1= i*n+k , x2=j*n+k,所以x2 - x1= (j-i)*n,x2-x1应该是n的倍数,但是根据之前的思路,我们已经知道x2-x1不可能是n的倍数,结论:任意的两个x%n都不可能相等,证毕。
这里其实也可以这样想,x1,x2...xn都在1~n-1之间,所以mod n就是原来的数,原数两两互不相等所以mod n后的余数也不可能两两相等。
3. 思路一:p有n个数,且一定与n互质,并且不会两两同余,而x也有n个数,且与n 互质,并且不会两两同余,所以说p,x 这两组数是同一组, 可能只是顺序有变化,当然是在mod n的前提下 认为相等,即对于任意的p,x一定存在 pi ≡ xj(mod n)。
思路二:证明p mod n(p除n的余数)与n互质。若此结论成立,则也有 pi ≡ xj(mod n)。
这里设 r=p mod n, r = a*xi -k*n, a*xi=k*n+r;这里判断r与n互质,其实就是让gcd(r,n)== 1
根据欧几里得原理 gcd(r,n)=gcd(k*n+r,n); 这里简单证明一下, 假设k*n+r和n的公约数为 j,
j | n , j | k*n+r , k*n一定能整除j 若加上r 也能整除j , 那么r一定也是j 的倍数才可以,所以 j | r.
gcd(r,n)=gcd(k*n+r,n).
因为a与n互质,xi也与n互质,a*xi也与n互质,所以gcd(a*xi,n)=1,所以gcd(r,n)=1;
所以p mod n的余数也与n互质 ,余数的取值范围也是在 1~n-1之间,也同样是n个与n互质的数,
所以一定会有 pi mod n= xj mod n, 即 pi ≡ pj(mod n).
所以p1*p2*p3*....pn ≡ x1*x2*x3*...xn(mod n);
a^Φ(n) (x1*x2*...xn) ≡ x1*x2*x3*...xn(mod n); 两边消去x1*x2*...xn;
a^Φ(n) ≡ 1(mod n)
到此,证毕。
若 n为质数(素数)即Φ(n)=n-1,并且a,n互质, a^(n-1) ≡ 1(mod n).这就是费马小定理。








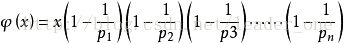














 959
959











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








