线索二叉树

在自学过程中，线索二叉树是继kmp算法之后的一大难题，在具体代码停了两天，就只想这个，想不出来，然后反复找资料看书，觉得可以得出一些眉目。以下是线索二叉树中序遍历线索化的递归函数重要代码：

if(!p->child){     //没有左孩子
p->LTag=Thread;    //前驱线索
p->lchild=pre;     //左孩子指针指向前驱
}
if(!pre->rchild){  //前驱没有右孩子
pre->RTag=Thread;  //后继线索
pre->rchild=p;     //前驱右孩子指针指向后继（当前节点p）
}
pre=p;             //保持pre指向p的前驱

 对每一句话都做了注释。以下是对于线索二叉树的图示说明，看起来确实很乱。

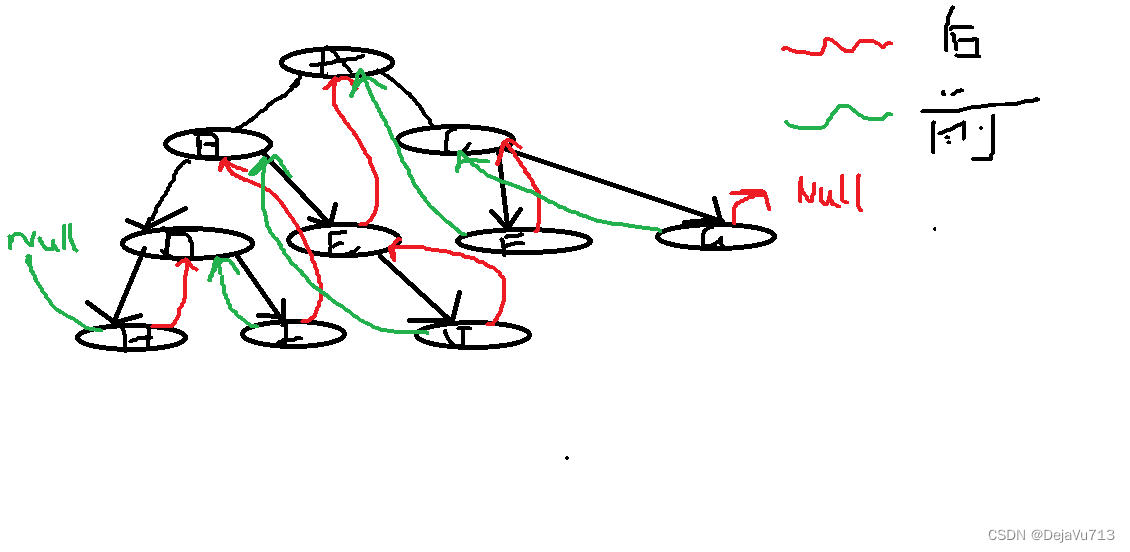
 在本子上也思索了很久，在查资料看到一个博主评论区回复pre定义问题,觉得说得很好，我摘抄下

//其实线索二叉树就是利用有空孩子的指针, 
//重新指向一段有效的空间(这里指前驱和后继), 
//如果要指向当前结点的前驱就必须要保存前驱结点,pre就充当了这个角色.
//pre的初始位置很重要, 因为第一个遍历到的没有左孩子的结点是没有前驱的, 
//因此就构造了一个头结点Thrt, 使pre初始指向它.
// 在InThreading线索化的过程中, 每遍历完当前的结点,
//  就需要更新pre的指向(pre=T), 因为刚遍历完的结点就成为了前驱结点,
//   因此我说"始终指向刚刚访问过的结点".

先不提增加一个头节点可以构成一个双向链表。就是在想前驱后继这个问题就让我够了。

于是我突然看小甲鱼举例时候拿前序遍历，那我想我这是中序遍历，那是不是可以按照中序思想。于是想了一下中序顺序是  左中右。按照编程思路从左开始，左没有，于是拿中作为前驱pre，这时左部分代码执行完毕，现在看中，如果中的rchild为空，那么左就是中的后继，这样就实现了前驱和后继。然后pre=p;将遍历完的节点成为前驱节点继续遍历下去，就可知上一个P的后驱。