本文试着用公式法,推出奇阶幻方的构造问题。就快捷构建幻方来说,公式法毫无优势。但作为并不多见的方法,值得一试。
一、通项公式和区间方程
首先,把幻方的格子看作几何点,过幻方中心点(格子)作互相垂直的两条坐标轴B、D(就是几何学上的xy轴),再过中心点作两条斜轴A、C(与对角线重合),在幻方方阵上,我们用连续的灰底格子代表这四条坐标,图中的字母A、B、C、D所在处,表示坐标正方向(图1)。

研究发现,四条坐标轴上的数字,可以根据如下坐标轴通项公式求得。
Nₘ=n₀±[Jm+2m(m-1) ]
[m= 0,1,2,…,(n-1)/2。]
式中,Nₘ表示坐标轴要填的数字,n₀=(1+n²)是所给数列的中项(即正中间数),J为一个常数,叫初进数,对应于A、B、C、D轴,分别为1、2、3、4。m是格子的序号,中心序号为0。坐标轴正方向,式子取+,负方向取-。只要把格子序号(均为正)代入公式,就可以求得该格子应该填的数字。
除了坐标轴,幻方的其他空格,即图1中的白格子,分为8个区间,每一个区间对应一条方程,分别是
N₁ =n₀+2x²-y
N₂ =n₀-x+y(2y+1)
N₃=n₀+x-2y(y-1)
N₄=n₀-2x²+y
N₅=n₀-2x(1-x)+y
N₆=n₀-x+2y(y+1)
N₇=n₀+x+y(1-2y)
N₈=n₀-2x(x+1)-y
各式中,x、y表示格子关于B、D轴(即x、y轴)的坐标,代入坐标,即可求得该格子应该填的数字。
二、具体填法
1、在正中格子,填写所给数列中项。以9阶幻方为例,则其正中间数n₀=(1+9²)/2=41。
2、填写各坐标轴正方向第一格,即m=1,则坐标轴通项公式简化为
Nₘ=n₀+J
也就是说,各坐标轴正方向第一格数字,就是中间数,加上其初进数J。即41分别加1,2,3,4,得42,43,44,45,即为A、B、C、D轴正方向的第一格数字,而各坐标轴负方向第一格,既可以用41减1,2,3,4得到40,39,38,37,也可以用互补数得到(本方法,各坐标轴上的数字,都是关于中心点互补的,即任意一对关于中心点对称的两数之和,都等于1+n²=1+9²=82)。
3、坐标轴其他数字
当然可以根据通项公式求得,但会较麻烦。经推导,各坐标轴正方向前后数字的关系,可由下式给出
Nₘ₊₁ =Nₘ+(Nₘ-N ₘ₋₁)+4
即各轴下一格要填的数字,是前一格数字,加上前两格数字的差,再加上4(负方向数字也用互补法求得)。这样,比公式求之会方便些。据此,我们求得9阶幻方各轴的数字如图2。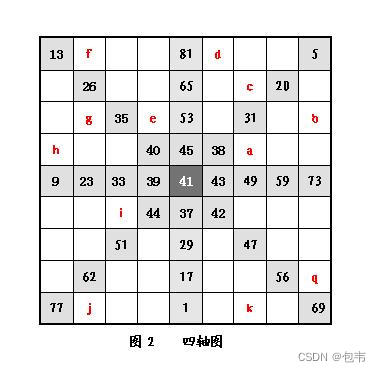
4、各区间数字求法举例
现在求图2各区间红色字母
1)一区域通项公式是
N=n₀+2x²-y
a点坐标是(2,1)
Na=n₀+2x²-y
=41+2×2²-1
=48 (比较图3,结果一样)
b坐标是(4,2)
Nb=n₀+2x²-y
=41+2×4²-2
=71 (比较图3,结果一样)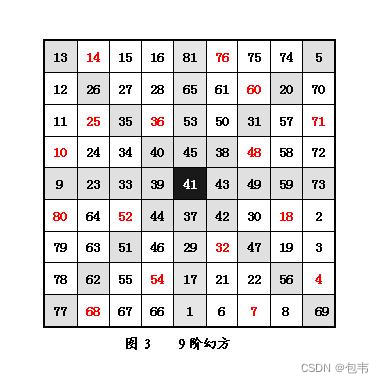
2)二区域通项公式是
N=n₀-x+y(2y+1)
c点坐标是(2,3)
Nc=n₀-x+y(2y+1)
=41-2+3(2×3+1)
=60 (比较图3,结果一样)
d点坐标是(1,4)
Nd=n₀-x+y(2y+1)
=41-1+4(2×4+1)
=76 (比较图3,结果一样)
3)三区域通项公式是
N=n₀+x-2y(y-1)
e点坐标是(-1,2)
Ne=n₀+x-2y(y-1)
=41+(-1)-2×2(2-1)
=36 (比较图3,结果一样)
f点坐标是(-3,4)
Nf=n₀+x-2y(y-1)
=41+(-3)-2×4(4-1)
=14 (比较图3,结果一样)
4)四区域通项公式是
N=n₀-2x²+y
g点坐标是(-3,2)
Ng=n₀-2x²+y
=41-2(-3)²+2
=25 (比较图3,结果一样)
h的坐标是(-4,1)
Nh=n₀-2x²+y
=41-2(-4)²+1
=10 (比较图3,结果一样)
5)五区域通项公式是
N=n₀-2x(1-x)+y
i点坐标是(-2,-1)
Ni=n₀-2x(1-x)+y
=41-2(-2)[1-(-2)]+(-1)
=52 (比较图3,结果一样)
6、六区域通项公式是
N=n₀-x+2y(y+1)
j点坐标是(-3,-4)
Nj=n₀-x+2y(y+1)
=41-(-3)+2×(-4)×(-4+1)
=68 (比较图3,结果一样)
7、七区域通项公式是
N=n₀+x+y(1-2y)
k点坐标是(2,-4)
Nk=n₀+x+y(1-2y)
=41+2-4×[1-2×(-4)]
=7 (比较图3,结果一样)
8、八区域通项公式是
N=n₀-2x(x+1)-y
q点坐标是(4,-3)
Nq=n₀-2x(x+1)-y
=41-2×4(4+1)-(-3)
=4 (比较图3,结果一样)。
其他还没验证的点,感兴趣的读者可以一试。注意区域的对应公式,坐标不要搞错。同样,用其他阶数的幻方检验,结果也是符合幻方要求的。下图的5阶幻方,非坐标轴数字,都可以验证方程。注意,对于n阶幻方来说,坐标轴格子是4n-3格,非坐标轴格子是n²-(4n-3)格,所以3阶幻方没有非坐标轴格。
研究发现,坐标轴通项公式和八个区间方程式,适用于所有以本方法构建的n阶幻方。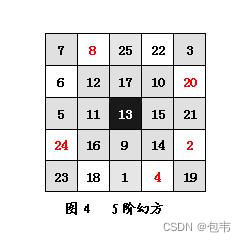







 本文通过公式法探讨奇阶幻方的构造,包括通项公式和区间方程,详细阐述如何填充各部分数字,适用于n阶幻方,帮助理解奇阶幻方的构建原理。
本文通过公式法探讨奇阶幻方的构造,包括通项公式和区间方程,详细阐述如何填充各部分数字,适用于n阶幻方,帮助理解奇阶幻方的构建原理。
















 2060
2060

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








