武忠祥教授考研数学超越90分-每日一题5月10日

解题思路：要求收敛域先求出收敛区间，再判断收敛区间两个端点处是否收敛。

第一步：求收敛区间

求收敛区间需要先求出收敛半径和中心点。

①求收敛半径：

公式如下：

因为中含有n次方，显然我们选择第二种公式更简单。

带入公式：

,把提出来计算

   ,（这里根据一个理论可以直接看出是等于3，我直接写总结里面了）

根据上面的理论，在n趋于无穷时，那么求出来了就是3，收敛半径就为。

②求中心点

根据左加右减收敛中心点就是1，

③求出收敛区间

收敛区间为（1-，1+）=（，）

第二步：判断收敛区间两端点是否收敛。

①我们先看，带入式子中：乘完再拆开

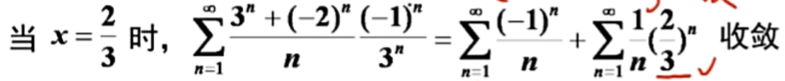
显然是个交错级数，根据莱布尼茨准则：

这里的就是,根据莱布尼茨准则，我们不难看出是收敛的也收敛，所以x=时是收敛的。

②我们再看x=的情况，带入式子中：

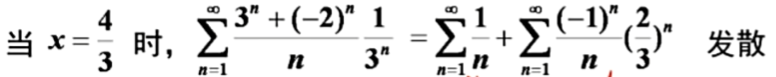
是调和级数，是发散的。

加上绝对值后就是所以也收敛，但是一个发散＋收敛还是发散。

所以收敛域就是

总结知识点

①收敛半径公式：

②莱布尼茨准则（交错级数）：

③调和级数是发散的：

④当n趋于无穷时，形如的极限：

（1）当a和b都是正数时，极限取决于老大；

（2）当a和b一个是正数一个是负数时，极限取决于绝对值大的。

例：的极限就是。

⑤当n趋于无穷时，x的n次方的极限，当x的绝对值大于1时是发散的，小于1时是收敛的。

⑥解题思路：要求收敛域先求出收敛区间，再判断收敛区间两个端点处是否收敛。