【SZU期末】大物慕课（下）

【SZU期末】大物慕课（下）

呜呜呜为什么会有大物慕课这种东西，要不是其他时间冲突了一定不选。
好难好难，听没有英文字幕的视频像听天书一样。

振动

常见词汇：

horizontal 水平的
amplitude 振幅
acceleration 加速度
phaseconstant 初相位
oscilation 振动
harmonic motion 简谐运动

 
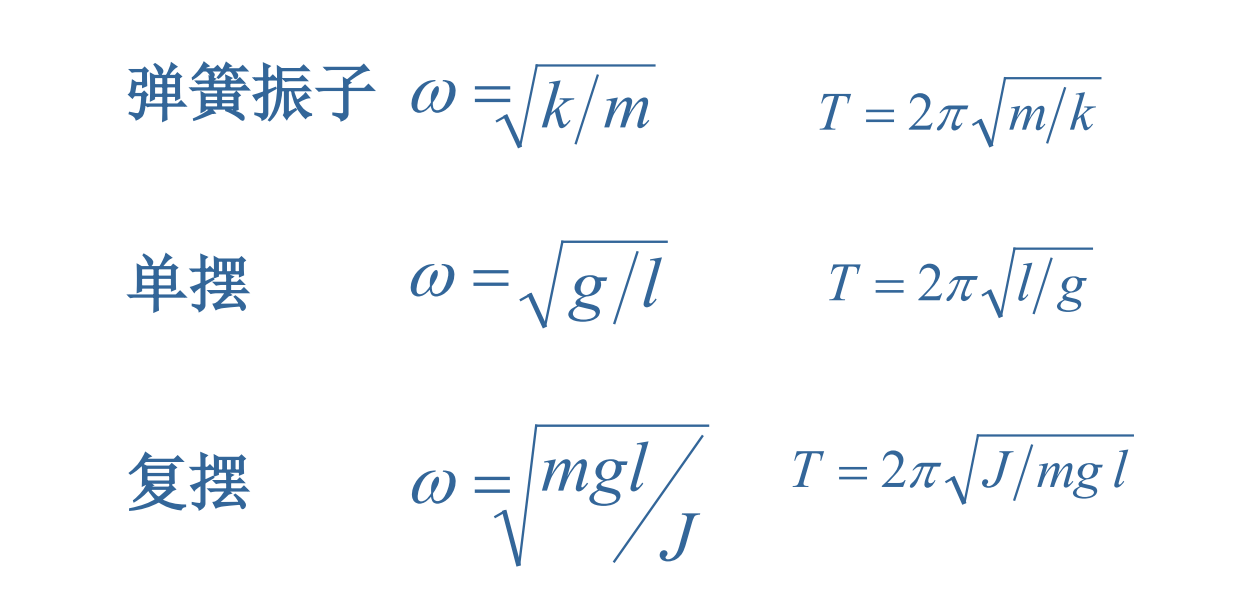
常用公式
位移：$x=A\cos \left(\omega t+{\phi }_0\right)$  

速度: $v=\frac{dx}{dt}=-A\omega \sin \left(\omega t+{\phi }_0\right)$

振幅: $A=\sqrt{x_0^2+\frac{v_0^2}{{\omega }^2}}$

角频率: $\omega =\sqrt{\frac{k}{m}}=\frac{2\pi }{T}$   

初相: ${\phi }_0$  相位: $\omega t+{\phi }_0$   $\tan {\phi }_0=\frac{-v_0}{\omega x_0}$

周期: $T=\frac{2\pi }{\omega }$  $T=2\pi \sqrt{\frac{L}{g}}$

频率: $f=\frac{1}{T}=\frac{\omega }{2\pi }$

速度: $v_{\max }=A\omega$  加速度: $a_{\max }=A{\omega }^2$

机械能 = 动能十势能  $E=\frac{1}{2}m{v}^2+\frac{1}{2}k{x}^2$  $E_{\text{总 }}=\frac{1}{2}k{A}^2$

弹簧串联: $\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}$ 弹簧并联:$k=k_1+k_2$

对于同一简谐运动：
$$\begin{array}{l}{x}_1=A\cos \left(\omega t_1+\phi \right)x_2=A\cos \left(\omega t_2+\phi \right)\\ \Delta \phi =\left(\omega t_2+\phi \right)-\left(\omega t_1+\phi \right)\\ \Delta t=t_2-t_1=\frac{\Delta \phi }{\omega }\end{array}$$

 

一些Mooc习题:

问题：电子以非相对论速度沿着z轴在+z方向上在接近零场的区域中移动。在t=0时，它到达原点<0，0，0>，并进入电场<0，0,，2X10^16V/m>的区域。你在＜5，3，0＞m的位置观察场。你首先观察辐射场是什么？
 
分析： 辐射场将以光速传播。假设观测点为P，原点为O。那么距离OP将为$\sqrt{(5\ast 5+3\ast 3)}=5.83m$，光覆盖所需时间$OP=5.83/3\ast 10^8=0.19$纳秒，因此辐射将在0.19纳秒内被观测到。

问题： 假设一个特定的理想质量弹簧系统的周期是2秒，如果质量增加三倍，系统的周期会是多少？
 
分析：$T\propto \sqrt{\frac{m}{k_s}}$ $2\ast \sqrt{3}=3.46s$

要掌握旋转矢量法

简谐运动

常用词汇

pivoted 转动的
pendulum 钟摆
rod 杆

常用公式：

合外力矩 = 转动惯量 * 角加速度   $\vec{M}=J\vec{\alpha }$

$\vec{M}=\vec{r}\times \vec{F}$ $M=rF\sin \theta$

单摆动力学分析：

$M=-mgl\sin \theta \approx -mgl\theta$

$-mgl\theta =J\frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}$  $J=m{l}^2$

$\frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}=-\frac{g}{l}\theta$  ${\omega }^2=\frac{g}{l}$

$\theta ={\theta }_{\mathrm{m}}\cos (\omega t+\phi )$

$T=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{l}{g}}$

复摆动力学分析：

$-mgl\theta =J\frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}$

${\omega }^2=\frac{mgl}{J}$

$T=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{J}{mgl}}$

简谐运动的合成

$A=\sqrt{A_1^2+A_2^2+2A_1{A}_2\cos \left({\phi }_2-{\phi }_1\right)}$

$\tan \phi =\frac{A_1\sin {\phi }_1+A_2\sin {\phi }_2}{A_1\cos {\phi }_1+A_2\cos {\phi }_2}$

机械波

常用词汇：

propagation 传播
Longitudinal mechanical waves 纵向机械波
displacement 位移
phase 相位

1. 横波：波传播方向上各点的振动方向与波传播方向垂直。
2. 纵波：波传播方向上各点的振动方向与波传播方向平行。
3. 简谐波： 波源及介质中各点均作简谐振动。

常用公式：
$$v=1/Tu=\frac{\lambda }{T}=\lambda v\lambda =\frac{u}{v}=Tu$$

• P点振动落后于O点振动，落后的时间为 $\Delta t=t_o-t_p=\frac{x}{u}$
• P点振动落后于O点振动，落后的位相为 $\Delta \phi ={\phi }_o-{\phi }_p=\frac{2\pi }{\lambda }x$
• 波动方程：
  $$y=A\cos \left[\omega \left(t-\frac{x}{u}\right)+{\phi }_0\right]$$$$y=A\cos \left[2\pi \left(ft-\frac{x}{\lambda }\right)+{\phi }_0\right]$$$$y=A\cos \left[\omega t+{\phi }_0-\frac{2\pi }{\lambda }\cdot x\right]$$

• 质元的振动速度，加速度：
  $$v=\frac{\partial y}{\partial t}=-\omega A\sin \left[\omega \left(t-\frac{x}{u}\right)+\phi \right]$$$$a=\frac{{\partial }^{2}y}{\partial t^2}=-{\omega }^{2}A\cos \left[\omega \left(t-\frac{x}{u}\right)+\phi \right]=-{\omega }^{2}y$$

$$V(y)=\sqrt{\frac{F_T(y)}{\mu }}=\sqrt{\frac{F_T(y)}{M/L}}=\sqrt{\frac{\mu yg}{\mu }}=\sqrt{yg}$$


波动能量的传播

• 波长划分：
  

• 振动动能
  $$\mathrm{d}{W}_{\mathrm{k}}=\frac{1}{2}(\mathrm{d}m)v^2=\frac{1}{2}(\rho \mathrm{d}V)v^2$$$$y=A\cos \omega \left(t-\frac{x}{u}\right)$$$$v=\frac{\partial y}{\partial t}=-\omega A\sin \omega \left(t-\frac{x}{u}\right)$$$$\mathrm{d}{W}_{\mathrm{k}}=\frac{1}{2}\rho \mathrm{d}V{A}^2{\omega }^2{\sin }^2\omega \left(t-\frac{x}{u}\right)$$

• 弹性势能
  $$\mathrm{d}{W}_{\mathrm{p}}=\frac{1}{2}k(\mathrm{d}y{)}^2$$$$\frac{F}{S}=E\frac{\Delta l}{l}$$$$F=k\Delta l$$$$k=\frac{SE}{l}=\frac{SE}{\mathrm{d}x}$$
  因此可以得出：$$\begin{array}{c}\mathrm{d}{W}_{\mathrm{p}}=\frac{1}{2}k(\mathrm{d}y{)}^2=\frac{1}{2}ES\mathrm{d}x{\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)}^2\\ =\frac{1}{2}\rho u^2\mathrm{d}V{\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)}^2\\ =\frac{1}{2}\rho \mathrm{d}V{A}^2{\omega }^2{\sin }^2\omega \left(t-\frac{x}{u}\right)=d{W}_k\end{array}$$

• 总机械能
  $$\mathrm{d}W=\mathrm{d}{W}_{\mathrm{k}}+\mathrm{d}{W}_{\mathrm{p}}=\rho \mathrm{d}V{A}^2{\omega }^2{\sin }^2\omega \left(t-\frac{x}{u}\right)$$

• 正弦波的平均功率
  $$P_{avg}=\frac{1}{2}\sqrt{\mu F}{\omega }^2{A}^2$$

• 波的强度
  $$I={\epsilon }_{0}c{E}^2$$
  (${\epsilon }_0=8.85\times 10^{-12}\frac{c^2}{{\mathrm{N}\cdot \mathrm{m}}^2}$)（$E$为电场强度）（$c=3\ast 10^8$)
  $$I=\frac{P}{S}=\bar{w}u$$$$I=\frac{1}{2}\rho A^2{\omega }^{2}u$$

折射率

波的衍射、干涉

波的衍射

波在传播过程中遇到障碍物，能绕过障碍物的边缘，在障碍物的阴影区内继续传播

波的干涉
频率相同、振动方向平行、相位相同或相位差恒定的两列波相遇时，使某些地方振动始终加强，而使另一些地方振动始终减弱的现象，称为波的干涉现象。

驻波

$$\begin{gathered} 正向:y_1=A\cos 2\pi \left(vt-\frac{x}{\lambda }\right) \\ 负向:y_2=A\cos 2\pi \left(vt+\frac{x}{\lambda }\right) \end{gathered}$$$$y=y_1+y_2$$$$=A\cos 2\pi \left(vt-\frac{x}{\lambda }\right)+A\cos 2\pi \left(vt+\frac{x}{\lambda }\right)$$$$=2A\cos 2\pi \frac{x}{\lambda }\cos 2\pi vt$$

• a
  $$\begin{gathered} 当\cos \frac{2\pi }{\lambda }x=0时A^{\prime }=0为波节 \\ x=(2k+1)\frac{\lambda }{4}(\frac{\lambda }{4}的奇数倍) \end{gathered}$$

• b
  $$\begin{gathered} 当\cos \frac{2\pi }{\lambda }x=\pm 1时\left|A^{\prime }\right|=2A为波腹 \\ x=2k\frac{\lambda }{4}(\frac{\lambda }{4}的偶数倍) \\ (k=0,\pm 1,\pm 2,\cdots ) \end{gathered}$$
  

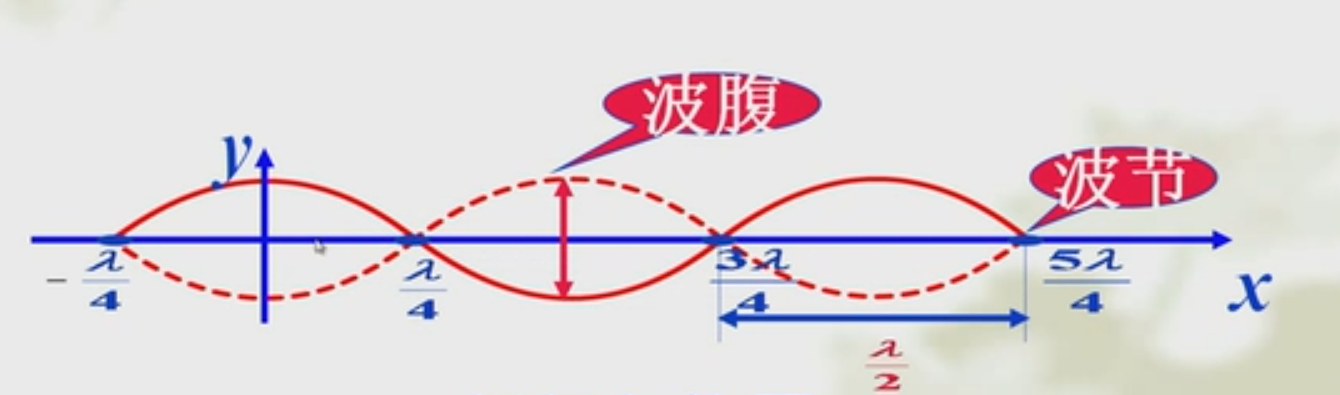
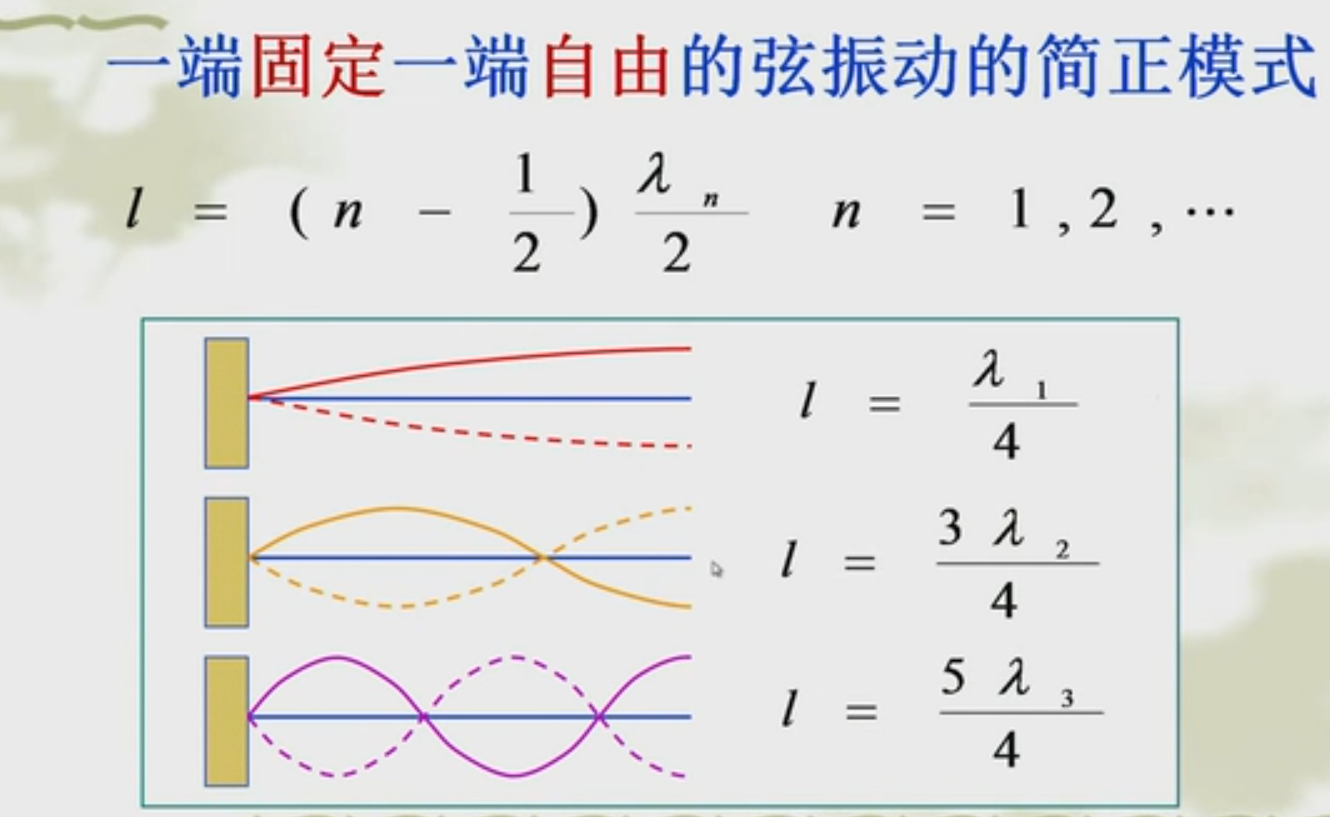
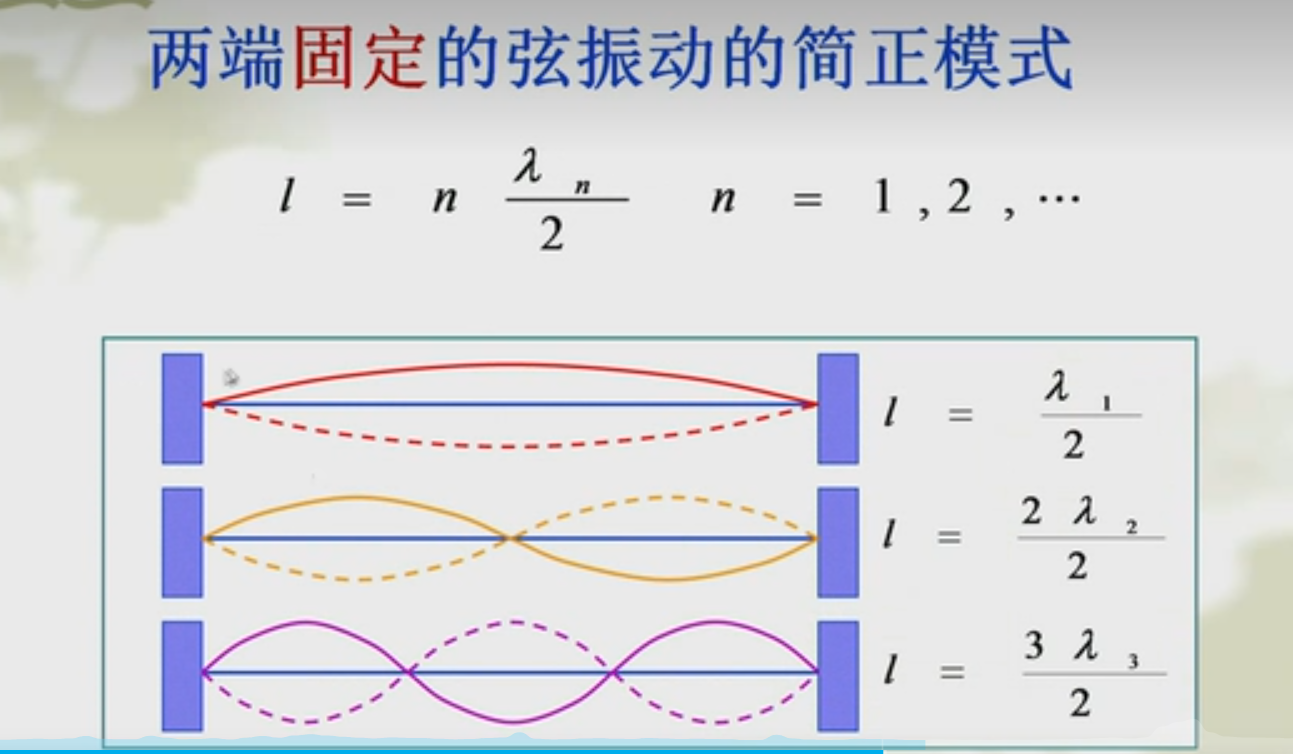
• 边界条件
  驻波一般由入射、反射波叠加而成，反射发生在两介质交界面上，在交界面处出现波节还是波腹，取决于介质的性质

• 介质分类
  波疏介质,波密介质

• 相位跃变(半波损失)
  当波从波疏介质垂直入射到波密介质被反射到波疏介质时形成波节。入射波与反射波在此处的相位时时相反，即反射波在分界处产生元 的相位跃变，相当于出现了半个波长的波程差，称半波损失.

• 波密介质 - 波疏介质
  当波从波密介质垂直入射到波疏介质，被反射到波密介质时形成波腹入射波与反射波在此处的相位时时相同，即反射波在分界处不产生相位跃

多普勒效应

① 波源不动，观察者相对介质以$v_0$运动

观察者接收的频率：

观察者向波源运动：$v^{\prime }=\frac{u+v_0}{u}v$

观察者远离波源运动：$v^{\prime }=\frac{u-v_0}{u}v$

② 观察者不动，波源相对介质以$v_s$运动

观察者接收的频率：

波源向观察者运动：$v^{\prime }=\frac{u}{u-v_s}v$

波源远离观察者运动：$v^{\prime }=\frac{u}{u+v_s}v$

LC振荡电路
$$T=2\pi \sqrt{LC}$$

波动光学

1. 可见光是电磁波：400nm~760nm

光的相关性

1. 两列光波相遇时发生干涉的必要条件

振动方向相同+频率相同+相位差恒定

2.由普通光源获得相关光的方法

分波面法和分振幅法

光程

光在介质中走过的路程与这种介质的乘积。

热学概论

$$\frac{PV}{T}=\frac{P_0{V}_0}{T_0}=\frac{P_0\frac{m^{\prime }}{M^{\prime }}{v}_0}{T_0}=\frac{P_0{v}_0}{T_0}\cdot \frac{m^{\prime }}{M}=R\frac{m^{\prime }}{M}$$
普适恒量：
$$R=\frac{P_0{V}_0}{T_0}=8.31\mathrm{J}\text{ / }\mathrm{mol}\cdot \mathrm{K}$$

$$PV=\frac{m^{\prime }}{M}RT=nRT=\frac{N}{N_A}RT$$

$$P=\frac{N}{V}\cdot \frac{R}{N_A}T$$
$$P=nkT$$

理想气体压强和温度公式

理想气体的统计假设

在平衡态下，气体分子运动各向同性，即分子向各个方向运动几率相等。

$${\bar{v}}_x={\bar{v}}_y={\bar{v}}_z=0$$

理想气体的温度公式

$$\begin{array}{l}p=\frac{2}{3}n\bar{\omega }\\ p=nkT\end{array}\}\bar{\omega }=\frac{3}{2}kT$$

理想气体内能

自由度

确定一个物体的空间位置所需要的独立坐标的数目

物体的自由度

自由运动的质点：自由度为3（3个平动+0个转动）

自由杆状物体：自由度为5（3个平动+2个转动）

自由运动的刚体：自由度为6（3个平动+3个转动）

刚性分子自由度

单原子分子：自由度为3（3个平动+0个转动）

双原子分子：自由度为5（3个平动+2个转动）

多原子分子：自由度为6（3个平动+3个转动）

理想气体内能

$$E=\frac{m^{\prime }}{M}\frac{i}{2}RT=\frac{i}{2}PV$$

内能改变：

$$\Delta E=\frac{m^{\prime }}{M}\frac{i}{2}R\Delta T=\frac{i}{2}\left(p_2{V}_2-p_1{V}_1\right)$$

• $i$ 为自由度

平均总动能

一个分子：$\frac{i}{2}kt$

1mol 分子：$N_A\frac{i}{2}kt=\frac{i}{2}Rt$

统计速率

（1）最概然速率$v_p$

讨论分子分布规律时

$${\frac{\mathrm{d}f(v)}{\mathrm{d}v}|}_{v=v_{\mathrm{p}}}=0$$

$$v_{\mathrm{p}}=\sqrt{\frac{2kT}{m}}=\sqrt{\frac{2RT}{M}}\approx 1.41\sqrt{\frac{RT}{M}}$$

物理意义：气体在一定温度下分布在最概然速率v,附近单位速率间隔内的相对分子数最多

（2）平均速率

分子碰撞规律

$$\begin{array}{rl}\bar{v}& =\frac{{\int }_0^{N}v\mathrm{d}N}{N}=\frac{{\int }_0^{\infty }vNf(v)\mathrm{d}v}{N}\\ & ={\int }_0^{\infty }vf(v)\mathrm{d}v\\ & =\sqrt{\frac{8kT}{\pi m}}\end{array}$$

（3）方均根速率

分子能量

$$\overline{v^2}=\frac{{\int }_0^N{v}^2\mathrm{d}N}{N}=\frac{{\int }_0^{\infty }{v}^{2}Nf(v)\mathrm{d}v}{N}=\frac{3kT}{m}$$$$\sqrt{\overline{v^2}}=\sqrt{\frac{3kT}{m}}=\sqrt{\frac{3RT}{M}}\approx 1.73\sqrt{\frac{RT}{M}}$$

$$v_0<v<\sqrt{v^2}$$

分子平均自由程:

每两次连续碰撞之间，一个分子自由运动的平均路程

分子平均碰撞次数:

单位时间内一个分子和其它分子碰撞的平均次数

单位时间内平均碰撞次数：

$$\bar{Z}=\pi d^{2}un$$

• 考虑其它分子的运动:

$$\bar{u}=\sqrt{2}\bar{v}$$

• 分子平均碰撞次数

$$\bar{Z}=\sqrt{2}\pi d^2\bar{v}n$$

• 平均自由程
  $$\bar{\lambda }=\frac{\bar{v}}{\bar{z}}=\frac{1}{\sqrt{2}\pi d^{2}n}=\frac{kT}{\sqrt{2}\pi d^{2}p}$$

热力学第一定律

过程曲线

	正	负
$\Delta E$	增加	减少
$W$	系统对外界做功	外界对系统做功
$Q$	系统吸热	系统放热

重要公式

$$Q=\Delta E+W$$$$dQ=dE+dW$$$$dE=\frac{m^{\prime }}{M}\frac{i}{2}RdT$$$$dW=pdV$$$$W={\int }_{V_1}^{V_2}\rho dV$$

摩尔热能量

定义: 1mol某种物质温度升高 1K 所吸收的热量

$$C={\left(\frac{dQ}{dT}\right)}_{\mathrm{mol}}$$

等容摩尔热容量

指 1mol 理想气体在等容过程下温度升高 1K 时所吸收的热量

$$C_V={\left(\frac{d{Q}_V}{dT}\right)}_{\mathrm{mol}}$$

$$\because dV=0,dW=0\therefore d{Q}_V=dE$$

$$dE=\frac{i}{2}RdT$$$$C_V=\frac{d{Q}_V}{dT}={\left(\frac{dE}{dT}\right)}_V=\frac{i}{2}R$$

等压摩尔热容量

指1mol理想气体在等压过程下，温度升高1K时所吸收的热量

$$C_P=\frac{d{Q}_P}{dT}=\frac{dE+pdV}{dT}=\frac{\frac{i}{2}RdT+RdT}{dT}=\frac{i}{2}R+R=C_v+R$$

比热容比

$$\gamma =\frac{C_p}{C_V}=\frac{i+2}{i}$$

对应过程热量的计算

$$Q=\nu C_V\left(T_2-T_1\right)(等容过程)$$

$$Q=\nu C_P\left(T_2-T_1\right)$$

等值过程

等容过程

特征: $dV=0$

规律：$\frac{p_1}{p_2}=\frac{T_1}{T_2}$

能量计算
$$\because dV=0\therefore dW=pdV=0$$

由热力学第一定律，得：

$$Q=E_2-E_1=\nu C_V\left(T_2-T_1\right)$$

等压过程

特征： $dP=0$

规律： $\frac{V_1}{V_2}=\frac{T_1}{T_2}$

能量计算：

$$\begin{array}{rl}W& ={\int }_{V_1}^{V_2}pdV\\ & =p\left(V_2-V_1\right)\\ & =\nu R\left(T_2-T_1\right)\end{array}$$$$Q=\nu C_P\left(T_2-T_1\right)=\nu \frac{i+2}{i}R(T_2-T_1)$$$$\Delta E=E_2-E_1=\nu \frac{i}{2}R\left(T_2-T_1\right)$$

等温过程

特征： $dT=0$

规律： $pV=C$

能量计算：

$\because \Delta T=0\therefore \Delta E=0$

由热力学第一定律得：

$$Q=W={\int }_{V_1}^{V_2}pdV$$

$$Q=W={\int }_{V_1}^{V_2}pdV={\int }_{V_1}^{V_2}\nu RT\frac{dV}{V}=vRT\ln \frac{V_2}{V_1}=\nu RT\ln \frac{p_1}{p_2}$$

绝热过程

$\Delta Q=0$

$\Delta E=-W$

$dE=-dW$

$$p{V}^{\gamma }=C$$$$pV=\frac{m^{‘}}{M}RT=CT$$$$T{V}^{\gamma -1}=C$$$$p^{\gamma -1}{T}^{-\gamma }=C$$

绝热线比等温线陡

$$dW=pdV=\frac{C}{V^{\nu }}dV$$
$$W=\frac{p_2{V}_2-p_1{V}_1}{1-\gamma }$$

$$Q_2=W_2+\Delta E_2=W_2-W_1<0放热$$
$$Q_3=W_3+\Delta E=W_3-W_1>0吸热$$

循环过程

物质系统经历一系列的变化过程又回到初始状态，这样的周而复始的变化过程称为循环过程

特点：初态=末态

$$\Delta E=0$$$$Q_{净}=W_{净}$$

$$Q_{\text{净 }}=Q_{\text{吸 }}-Q_{\text{放 }}=Q_1-Q_2$$$$W_{\text{净 }}=W_{\text{系统对外 }}-{\mathbf{W}}_{\text{外对系统 }}$$

循环效率

$$\eta =\frac{W}{Q_1}=\frac{Q_1-Q_2}{Q_1}=1-\frac{Q_2}{Q_1}$$

制冷系数

$$e=\frac{Q_2}{W}=\frac{Q_2}{Q_1-Q_2}$$

• $W$:外界对工质作功

• $Q_2$.:从低温热源吸热

卡诺循环

卡诺制热

$$Q_1=\mathbf{v}{T}_1\ln \frac{V_2}{V_1}{Q}_2=\mathbf{v}{T}_2\ln \frac{V_3}{V_4}$$$$T_1{V}_2^{\gamma -1}=T_2{V}_3^{\gamma -1}{T}_1{V}_1^{\gamma -1}=T_2{V}_4^{\gamma -1}$$
$$\frac{V_2}{V_1}=\frac{V_3}{V_4}⟹\frac{Q_1}{Q_2}=\frac{T_1}{T_2}$$
$$\text{ 则卡诺循环的热机效率为: }{\eta }_c=1-\frac{Q_2}{Q_1}=1-\frac{T_2}{T_1}$$

卡诺制冷

$$e_c=\frac{Q_2}{W}=\frac{Q_2}{Q_1-Q_2}=\frac{T_2}{T_1-T_2}$$

热力学第二定律