【期末复习】例题讲解Dijkstra算法

使用场景

Dijkstra算法用于解决单源点最短路径问题，即给一个顶点作为源点，依次求它到图中其他n-1个顶点的最短距离。

例题讲解

Dijkstra算法将图中所有顶点分成两部分，第一部分是已知到源点最短距离的顶点Known(K)，第二部分是不知道到源点最短距离的顶点Unknown(U)。初始化K中只有源点一个顶点，U中有n-1个顶点。如下图，我们求源点1到终点7的最短路径。

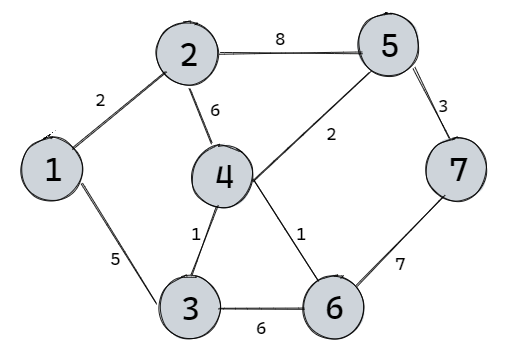
根据上图，可以得到如下表：

K	K中顶点到源点的距离	U	U中顶点到源点的距离
1	0	2	无穷
		3	无穷
		4	无穷
		5	无穷
		6	无穷
		7	无穷

1-1. 找到顶点1的邻接点2和3，然后更新它们到源点1的距离得到下表

K	K中顶点到源点的距离	U	U中顶点到源点的距离
1	0	2	2
		3	5
		4	无穷
		5	无穷
		6	无穷
		7	无穷

1-2. 更新K,U中的顶点。发现U中2到源点的距离最小，把2加入K中得到下表

K