数据结构与算法---查找

查找表

同一类型的数据元素（或记录）构成的集合

关键字：用来标识一个数据元素（或记录）的某个数据项的值

查找表分类：

• 线性表
• 树表
• 哈希表

静态和动态：

• 静态查找表：仅作查询，检索操作的查找表
• 动态查找表：作插入和删除操作的查找表

平均查找长度：关键字的平均比较次数

线性表

顺序查找

顺序表或线性表表示的静态查找表，表内元素无序

在顺序表S中查找值为key的数据元素，从最后一个元素开始比较

改进：把待查关键字key存入表头S[0]作哨兵

当S.length较大时，此方法可以使一次查找所需的平均时间几乎减少一半

顺序查找表的定义

#define MAXSIZE  100
typedef int KeyType;
typedef int InfoType;
struct Keytype
{
	KeyType key;   //关键字域
	InfoType otherinfo;  //其他域
};
struct SSTable  //顺序表结构类型定义
{
	Keytype* R;  //顺序表地址指针（包括关键字域和其他域）
	int length;   //定义顺序表长度
};

顺序查找算法

int SqSearch(SSTable& S, const KeyType e)
{
	//第一步：施加哨兵
	S.R[0].key = e;
	//第二步：顺序比较查找
	int i;
	for (i = S.length; S.R[i].key != e; --i)
	{
		; //空操作
	}
	return i;
	//时间复杂度O(n)、空间复杂度O(1)，ASL=(n+1)/2
}

优缺点

优点：算法简单，逻辑次序无要求，且不同存储结构均适用

缺点：ASL太长，时间效率太低

如何提高查找效率

1. 按查找概率高低存储
   • 查找概率高，比较次数少
   • 查找概率低，比较次数多
2. 当查找概率无法确定时
   • 按查找概率动态调整
   • 在每个key中增设一个访问频度域
   • 始终保持频度域按非递增，有序的次序排列
   • 每次查找后，讲刚查到的key数据移至表头

折半查找

集合中的元素按递增的顺序排列

每次将待查记录所在区间缩小一半

mid=(low+high)/2

key<mid, high=mid-1
key>mid, low=mid+1

若key==mid, 查找成功
若high<low, 查找失败

折半查找算法(非递归）

设表长为n，low，high和mid分别指向待查元素所在区间的上界，下界和中点，key为给定的要查找的值

初始时，令low=1，high=n，
mid=（low+high）/2

int Search(SSTable& S, const KeyType e)
{
	int low = 1, high = S.length;  //设置表头和表尾指针
	while (low<=high)  //low>high，循环结束
	{
		int mid = (low + high) / 2;
		if (e == S.R[mid].key)
			return mid;  //e的位置就等于中间位置
		if (e < S.R[mid].key)
			high = mid - 1;  //e的值位于小半部分，high指针前移
		if (e > S.R[mid].key)
			low = mid + 1;  //e的值位于大半部分，low指针后移
	}
	return -1;  //查找失败，返回-1
}

折半查找算法(递归)

int Search_(SSTable& S, const KeyType e,int low,int high)
{
	if (low > high)  //递归的终止条件
		return -1;
	int mid = (low + high) / 2;
	if (e == S.R[mid].key)
		return mid;
	if (e < S.R[mid].key)
		return Search_(S, e, low, mid - 1);
	else
		return Search_(S, e, mid+1, high);
}

优缺点

优点：效率比顺序查找高

缺点：只适用于有序表，且仅限于顺序存储结构，对线性链表无效

分块查找

也称索引顺序查找，将表分为几块，且表或者有序，或者分块有序

查找过程：先确定待查元素所在块（顺序查找或折半查找），再在块内进行顺序查找

数据类型定义

#define MAXBLOCK 18  //设置表长为18，0下标不存放元素，从1开始到18,每6个分一块，线性表分为3块
typedef int Keytype;

//每一个索引表的位置包括数据域，起始位置域，终止位置域
 struct Elemtype
{
	Keytype key;  
	int start, end;
};
 //索引表结构类型定义
 struct IndexTbale {  
	Elemtype *index;
	int length;
};
 //索引表的初始化
 bool InitList(IndexTbale &T)
 {
	T.index = new Elemtype[MAXBLOCK];  //在堆区开辟内存 使用new定义
	 if (!T.index) {  //没有表头，说明索引表不存在
		 cout << "error" << endl;
		 return false;
	 }
	 T.length = 0;  //索引表初始长度
	 return true;
 }

分块查找算法

 int Blocksearch(IndexTbale& T, Keytype *a, Keytype e)  //a是输入的元素数据表，e是要查找的值
 {
	 int left = 1;
	 int right = T.length;  //right指向索引表的末端
	 while (left <= right) {
		 int mid = (left + right) / 2;   //先把索引表对半分？进行二分查找？
		 if (e <=T.index[mid].key) { //如果小于mid,则需要判断是否大于mid-1
			 if (e >T.index[mid - 1].key) { //如果大于mid-1 说明在mid所在块
				 //遍历查找元素在索引表所在块的起始位置到终止位置
				 for (int i = T.index[mid].start;i <= T.index[mid].end; i++) {
					 if (e == a[i])
						 return i; //进行顺序搜索
				 }
				 return 0; //在所在块找不到此元素，返回0
			 }
			 else { //查找元素小于等于mid-1 则需要进行下次的折半查找
				 right = mid - 1;
			 }
		 }
		 else { // 查找元素大于mid，进行下一次折半查找
			 left = mid + 1;
		 }
	 }
	 return 0; // while循环后依旧没有return，说明没有找到，返回0
 }

测试案例

#include <iostream>
using namespace std;
int main()
{
    IndexTbale T;  //定义索引表T
	InitList(T);   //初始化索引表T
	Creat(T);   //创建数据表
	Keytype a[19] = { 0, 22, 12, 13, 8, 9, 20, 33, 42, 44,
		38, 24, 48, 60, 58, 74, 57, 86, 53 };
    T.length = 3;  //输入18个元素，每6个元素分为一块，索引表分为3块，长度为3
	T.index[1].start = 1, T.index[1].end = 6, //索引表第一块从1开始，到6结束
    T.index[1].key = 22;  //每一块位置的数据域存储6个元素中的最大值
	T.index[2].start = 7, T.index[2].end = 12,
    T.index[2].key = 48;
	T.index[3].start = 13, T.index[3].end = 18,
    T.index[3].key = 86;

	cout << "输入要查找的元素：" << endl;
	int e;
	cin >> e;
	int x = Blocksearch(T, a, e);
	cout << "该元素在第" << x << "个位置" << endl;

	system("pause");
	return 0;
}

算法效率分析

优缺点

优点：插入和删除比较容易，无需进行大量移动

缺点：要增加一个索引表的储存空间并对初始索引进行排序运算

适用情况：如果线性表要快速查找且又经常动态变化，则可采用分块查找

线性表查找方法比较

	顺序查找	折半查找	分块查找
ASL	最大	最小	适中
结构	有序表，无序表可	仅有序表	分块有序
存储结构	循序表，链表都可	链表不可	顺序表，链表都可

树表

当表插入，删除操作频繁时，为维护表的有序性，需要移动表中很多记录，有一种方法就是改用动态查找表–树表

对于给定的key值，若表中存在则成功返回，若不存在则插入一个等于key值的记录

二叉排序树

二叉排序树或是空树，或是满足如下性质的二叉树：

• 若其左子树非空，则左子树上所有节点的值均小于根节点的值
• 若其右子树非空，则右子树上所有节点的值均大于等于根节点的值
• 其左右子树本身又是一颗二叉排序树

如果中序遍历非空二叉排序树，所得到的元素数据序列是一个递增的有序数列

数据类型定义

typedef int BSTKeytype;
typedef char* info;
typedef struct Elemtype
{
	BSTKeytype key;
	info other;
};
typedef struct Node  //树中每一个结点包括数据域（key元素域和other其他域），左孩子和右孩子
{
	Elemtype data;
	Node* lchild, * rchild;
}*BSTree;

递归创建二叉树

void Creat(BSTree& T)
{
	int input;
	cin >> input;
	if (input == 0)
		T = NULL;
	else {
		T = new Node;
		T->data.key = input;
		Creat(T->lchild);
		Creat(T->rchild);
	}
}

二叉排序树的递归查找

1. 若二叉排序树为空，查找失败，返回空指针
2. 二叉排序树非空，将给定值key与根节点的关键字
   T->data.key比较
   • 若key==T->data.key，查找成功，返回根节点地址
   • 若key>T->data.key，进一步查找右子树
   • 若key< T->data.key，进一步查找左子树

比较的关键字次数=此结点所在层次数

最多的比较次数=树的深度

BSTree& Search(BSTree& T, const BSTKeytype& e)
{
	if (!T || T->data.key == e)
		return T;
	else if (e < T->data.key)
		return Search(T->lchild, e);
	else
		return Search(T->rchild, e);
}

二叉排序树查找算法分析

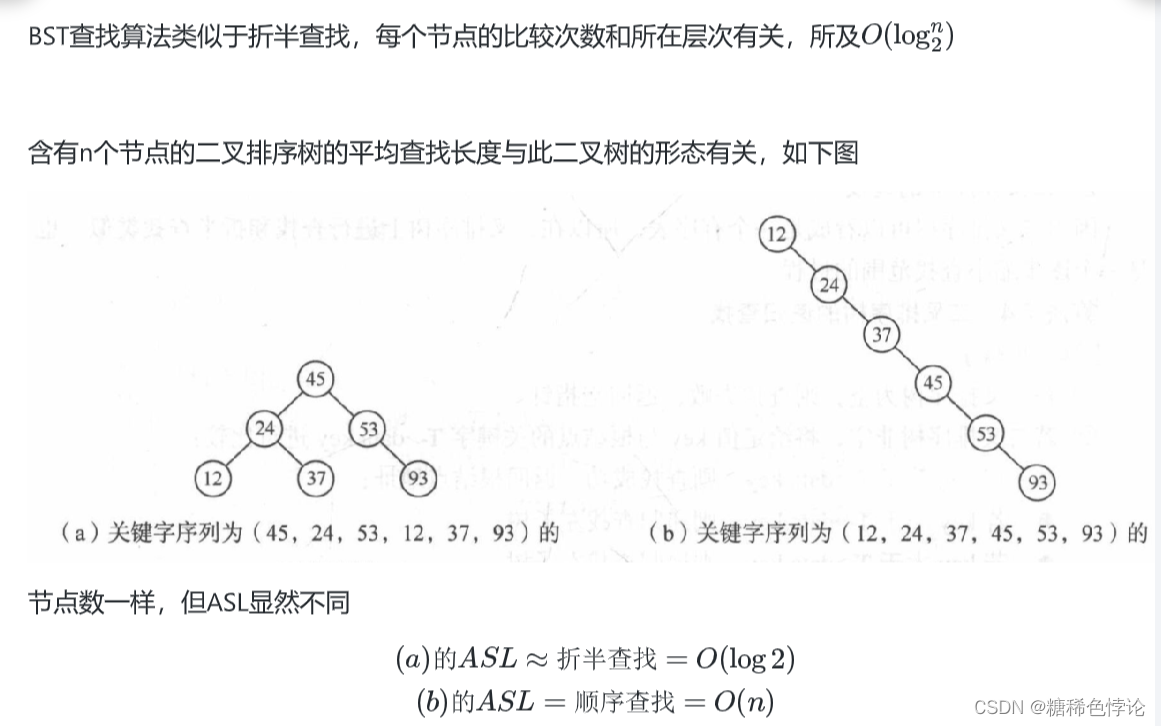
所以说在创建二叉排序树的时候，尽量要让此二叉树形状均匀

二叉排序树上插入操作

若树为空，则插入节点作为根节点插入到空树中

否则，继续在其左子树，右子树上查找（若树中已有，不再插入）

树中没有此元素，查找直至某个叶子节点的左子树或右子树为空为止，则插入节点应为该叶子节点的左孩子或右孩子

插入的元素一定在叶子节点上

void InsertBSTree(BSTree& T, BSTKeytype e)
{
	if (T == NULL) {
		T = new Node;
		T->data.key = e;
		T->lchild = T->rchild = NULL;
	}
	else if (e < T->data.key)
		InsertBSTree(T->lchild, e);
	else if (e > T->data.key)
		InsertBSTree(T->rchild, e);
	
}

二叉排序树的创建

void CreatBSTree(BSTree& T)
{
	cout << "为二叉排序树输入元素（以0为结束标志）：" << endl;
	T = NULL;
	BSTKeytype key;
	cin >> key;
	while (key!=0)
	{
		InsertBSTree(T, key);
		cin >> key;
	}
}

二叉排序树上删除操作

删除该节点，并且保证删除后所得的二叉树仍满足二叉排序树的性质

将因删除节点而断开的二叉链表重新连接起来

防止重新连接后树的高度增加

1. 被删除的节点是叶子节点：直接删除该节点，其双亲节点中相应指针域的值改为空
2. 被删除的节点只有左子树或者只有右子树：用其左子树或右子树的节点替换
3. 被删除的节点既有左子树，也有右子树：
   • 以其中序前驱替换之，然后删除该前驱节点，前驱是左子树中最大的节点
   • 用其后继替换之，然后再删除该后继节点，后继是右子树中最小的节点

若已知一个二叉排序树的节点m，m的直接前驱节点为m的左子树上右分支最后一个右孩
子为空的节点，如下图

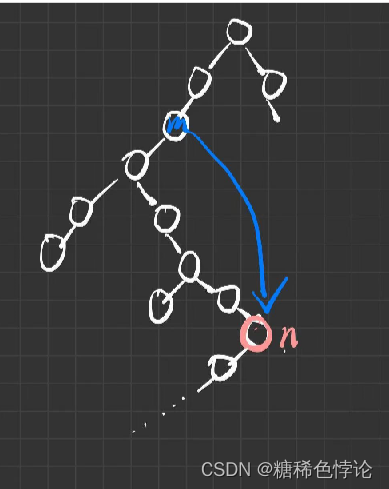
由图可知，n没有右孩子(如果n一旦有了有孩子，那么m的直接前驱必然会发生变化)，但n可以有左孩子(即使有左孩子也并不影响n是m的直接前驱)，同时也要考虑n的左子树没有右分支的情况

如果n没有右分支，那么m的直接前驱为n

利用对称性可知直接后继节点则为：m的右子树上左分支上最后一个左孩子为空的节点

void Delete(BSTree &T, BSTKeytype key)
{
	BSTree p = T;
	BSTree parent = NULL;
	while (p) {
		if (p->data.key == key)
			break;  //退出循环，此时p指向要删除的结点
		else if (key < p->data.key) {
			parent = p;  //通过比较key值定位要删除节点
			p = p->lchild;
		}
		else {
			parent = p;
			p = p->rchild;
		}
	}
	if(!p){
	cout << "树中没有此结点" << endl;
	}
 //当控制来到次行时，说明p指向了要删除的节点
	BSTree pfree;
	BSTree node;
	if (p->lchild && p->rchild) {
		BSTree prior = p->lchild;//p的直接前驱一定在p的左子树上
		BSTree parentprior = p; //需要一个节点来定位prior的双亲结点
		while (prior->rchild) {
			parentprior = prior;
			prior = prior->rchild;
		}
		p->data.key = prior->data.key;

		if (parentprior != p)
		{
			parentprior->rchild = prior->lchild;
		}
		else {
			parentprior->lchild = prior->lchild;
		}
		delete prior;
		return;
	}
	else if (!p->lchild) {
		pfree= p; // pfree用于存放 要删除节点的地址
		node = p->rchild;  // node存放需要链接节点的地址
	}
	else if (!p->rchild) {
		pfree= p;
		node = p->lchild;
	}
	//如果parent域仍然为空，说明要删除的节点为根节点
	if (!parent) {
		T = node;
	}
	else if (parent->lchild == p) {
		parent->lchild = node;
	}
	else {
		parent->rchild = node;
	}
	delete pfree;
}

平衡二叉树（AVL树）

一棵平衡二叉树或者空树，或者具有下列性质的二叉排序树：

平衡因子（BF）=节点左子树的高度-节点右子树的高度

左子树与右子树的高度之差的绝对值小于等于1

左子树与右子树也是平衡二叉排序树

对于一棵有n个节点的AVL树，其高度保持在O(log2^n)数量级
ASL也保持在O(log2^n)量级

如果在一棵AVL树中插入一个新节点后造成失衡，则必须重新调整树的结构，使之恢复平衡

失衡二叉排序树平衡调整的四种类型

LL型旋转(右旋转)

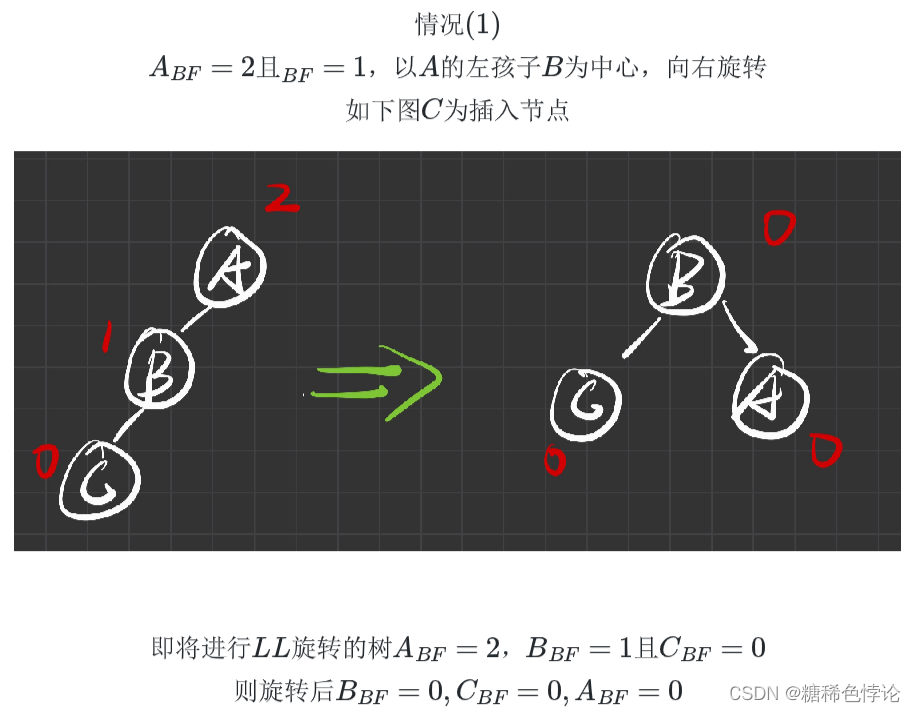
2.

RR型旋转(左旋转)

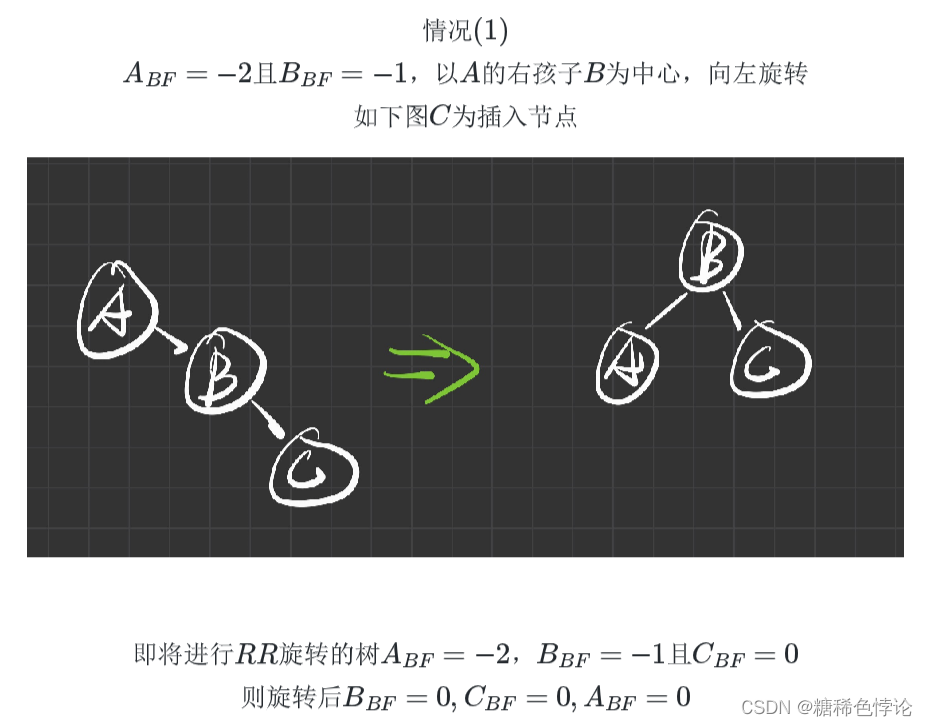
2.

LR型旋转(左右旋转)

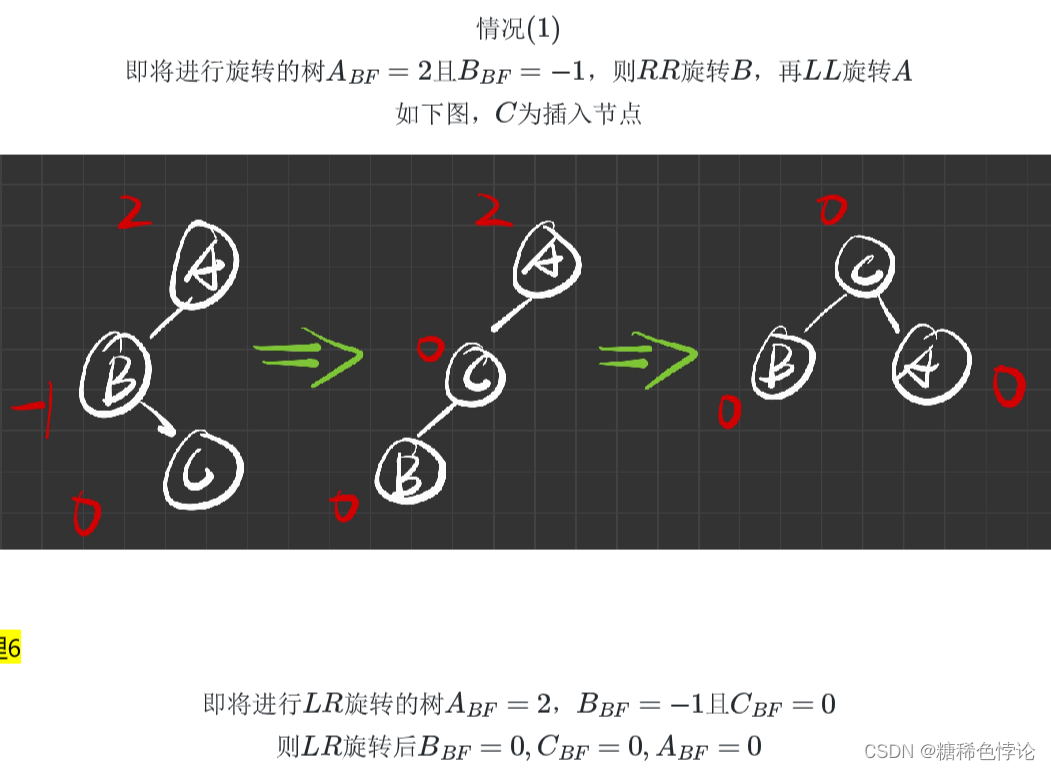
2.


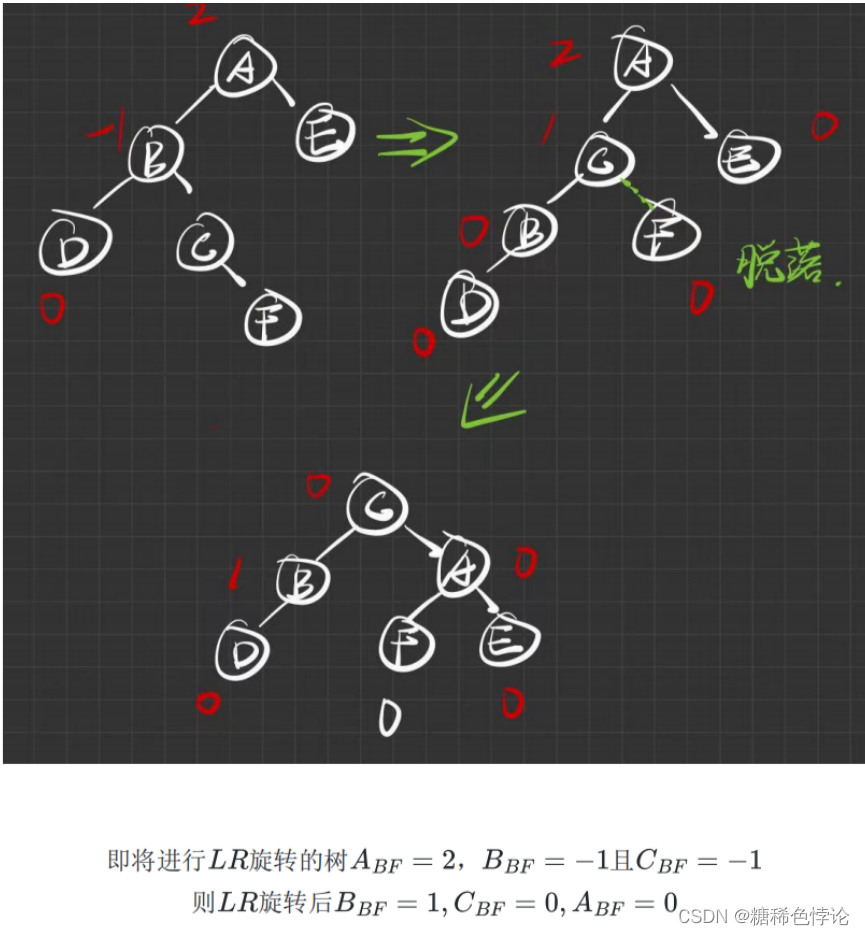
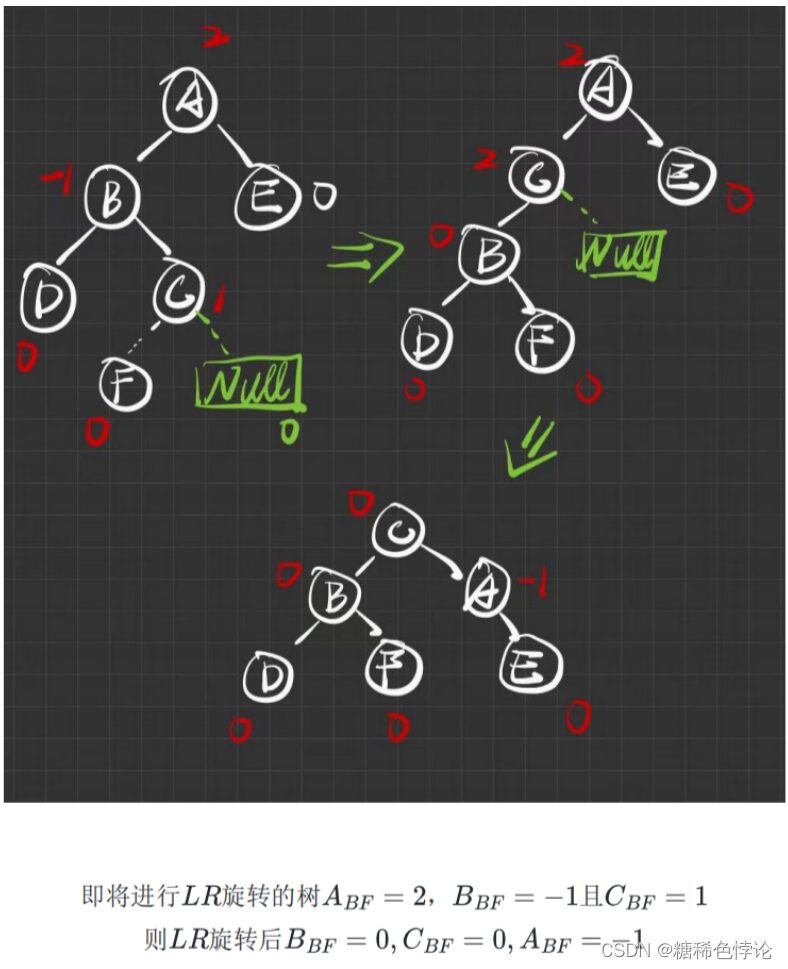
3.

RL型旋转(右左旋转)

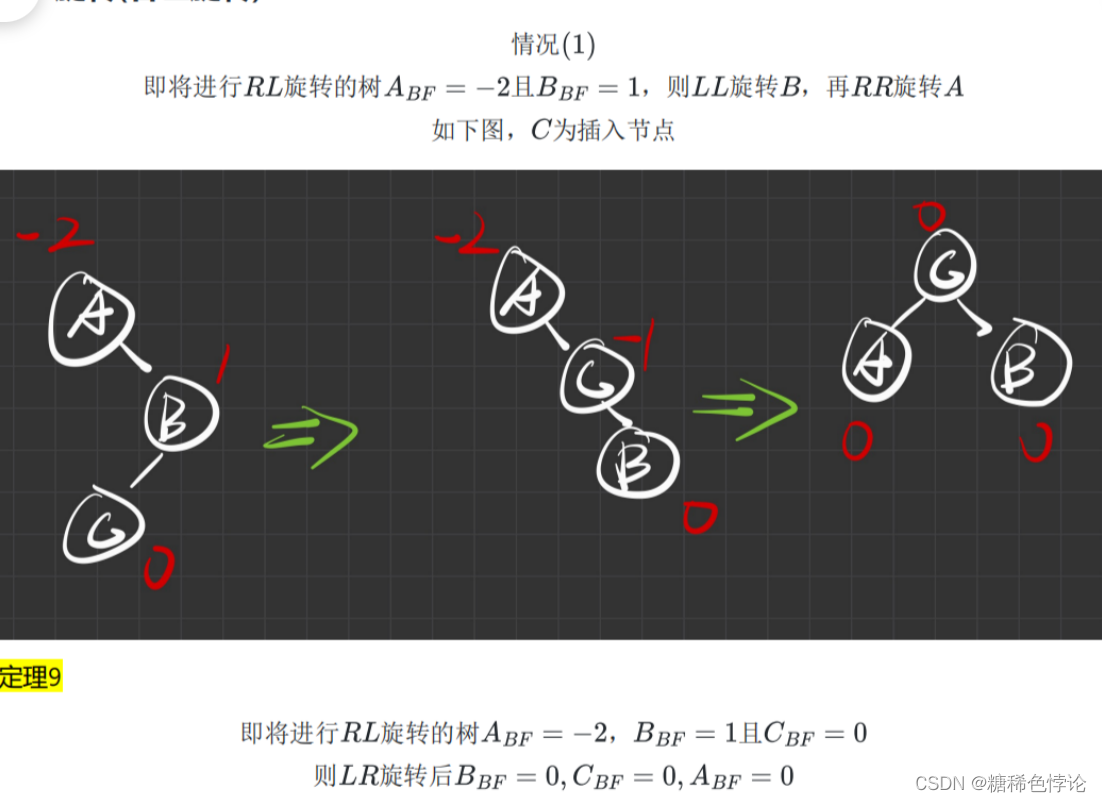
2.

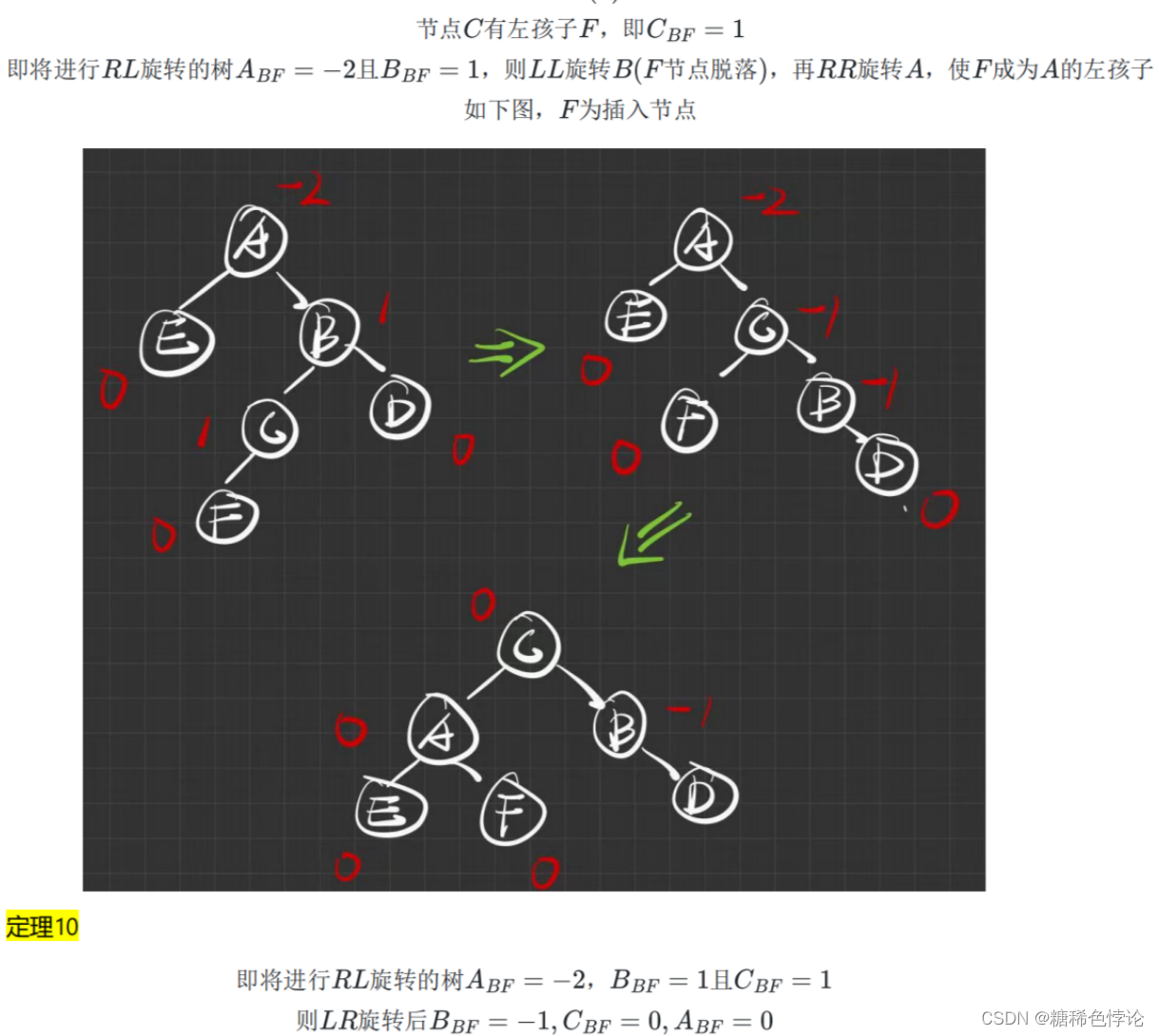
3.

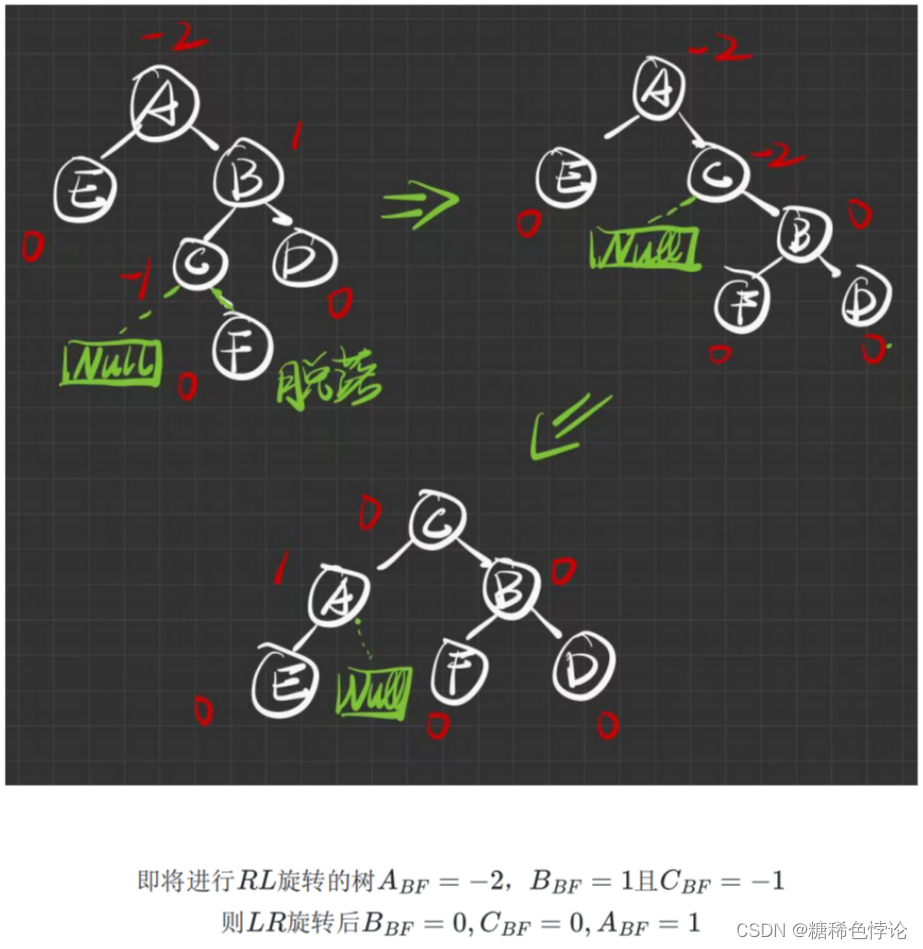
总结

平衡二叉树代码

#define LH 1 //平衡因子1
#define EH 0 //平衡因子0
#define RH -1 //平衡因子-1
typedef int AVLElemtype;
typedef struct AVLNode
{
	AVLElemtype key;
	int bf;  //平衡因子
	AVLNode * lchild, *rchild;
}*AVLTree;

//左旋转树 代表着：以 的右孩子为中心，向左旋转
void LeftRotate(AVLTree& T)
{
	AVLTree Rchild = T->rchild;
	T->rchild = Rchild->lchild;
	Rchild->lchild = T;
	T = Rchild;
}
//右旋转树 代表着：以 的左孩子为中心，向右旋转
void RightRotate(AVLTree& T)
{
	AVLTree Lchild = T->lchild;
	T->lchild = Lchild->rchild;
	Lchild->rchild = T;
	T = Lchild;
}
//平衡二叉树大体上可以分成左平衡(LL,LR)和右平衡(RR,RL)
//左平衡
void LeftBalance(AVLTree& T) {
	AVLTree L = T->lchild; // L->bf绝对不可能为EH(定理1)
	AVLTree Lr;
	// T的左孩子的右孩子
	switch (L->bf) {
		// LL 旋转
	case LH:
		//! 定理2
		T->bf = L->bf = EH;
		//! 此行的上下两行不可对调
		RightRotate(T);
		break;
	case RH:
		// LR旋转
		Lr = L->rchild; //
		switch (Lr->bf) {
		case LH:
			//定理8
			T->bf = RH;
			L->bf = EH;
			break;
		case EH:
			//定理6
			T->bf = L->bf = EH;
			break;
		case RH:
			//定理7
			T->bf = EH;
			L->bf = LH;
			break;
		}
		//根据定理6，7，8可知，旋转后Lr的BF必定为0
		Lr->bf = EH;
		LeftRotate(T->lchild);
		RightRotate(T);
		break;
	}
}
//右平衡
// 和左平衡同理
void RightBalance(AVLTree& T) {
	AVLTree R = T->rchild;
	AVLTree Rl;
	switch (R->bf) {
	case RH:
		T->bf = R->bf = EH;
		LeftRotate(T);
		break;
	case LH: {
		Rl = R->lchild; //
		switch (Rl->bf) {
		case LH:
			T->bf = EH;
			R->bf = RH;
			break;
		case EH:
			T->bf = R->bf = EH;
			break;
		case RH:
			T->bf = LH;
			R->bf = EH;
			break;
		}
		Rl->bf = EH;
		RightRotate(T->rchild);
		LeftRotate(T);
	}
	}
}

//插入结点和及时平衡
//! 全局变量taller记录高度是否发生变化，如果未发生变化为false，发生则true
bool taller = false;
void Insert_AVL(AVLTree& T, AVLElemtype key, bool& taller)
{
	// T为要插入节点的双亲节点，key为要插入数据的值
	//若T为空，则创建一个节点，并初始化
	if (T == NULL)
	{
		T = new AVLNode;
		T->lchild = T->rchild = NULL;
		T->key = key;
		T->bf = EH;
		taller = true;
	}
	else if (key < T->key) {
		//如果插入值小于T的key值，则递归T的左子树，直到找到一个NULL节点
		Insert_AVL(T->lchild, key, taller);
		//判断树是否变高了
		if (taller) {
			//以T为根插入节点，则T的bf发生变化
			switch (T->bf) {
			case LH:
				// T的bf == -1，向T的左孩子插入节点则T的bf = 2，需要左平衡
				LeftBalance(T);
				taller = false;
				//经过平衡后taller = false，因为T经过左调整后，变得平衡了
				break;
			case EH:
				// 如果T的bf == 0，向T的左孩子插入节点，则T的bf = 1
				T->bf = LH;
				//此时T的高度发生变化
				taller = true;
				break;
			case RH:
				// 如果T的bf == -1，向T的左孩子插入节点，则T的bf = 0
				T->bf = EH;
				//高度未发生变化
				taller = false;
				break;
			}
		}
	}
	else{
		//和上面同理
		Insert_AVL(T->rchild, key, taller);
		if (taller) {
			switch (T->bf) {
			case LH:
				T->bf = EH;
				taller = false;
				break;
			case EH:
				T->bf = RH;
				taller = true;
				break;
			case RH:
				RightBalance(T);
				taller = false;
				break;
			}
		}
	}
}

创建平衡二叉树

void CreatAVL(AVLTree& T)
{
	cout << endl << "为平衡二叉树输入元素（以0为结束标志）：" << endl;
	T = NULL;
	AVLElemtype key;
	cin >> key;
	while (key != 0) 
	{
		Insert_AVL(T, key, taller);
		cin >> key;
	}
}
//中序遍历
void LDR_(AVLTree& T)
{
	if (T == NULL)
		return;
	else {
		LDR_(T->lchild);
		cout << T->key << "(" << T->bf << ")" << "  ";
		LDR_(T->rchild);
	}
}

测试代码

#include <iostream>
using namespace std;
int main(void)
{
	AVLTree T;
	CreatAVL(T);
	cout << "中序遍历平衡二叉树：" << endl;
	LDR_(T);
	cout<< endl<< "先序遍历平衡二叉树：" << endl;
	DLR_(T);
	cout << endl;

	system("pause");
	return 0;
}

output：

哈希表

记录的存储位置与关键字直接存在对应关系

Loc(i)=Hash(keyi)

散列方法：选取某个函数，依该函数按关键字计算元素的存储位置，并按此存放，查找时，由同一个函数对给定值k计算地址，与地址单元中元素关键码相比较

冲突：通过Hash函数，不同的关键字映射到同一个地址上（不可避免，只能尽量减少）

优点：查找效率高

缺点：空间效率低

构造hash函数考虑的因素

• 执行速度(计算时间)
• 关键字长度
• Hash Table的大小
• 关键字的分布情况
• 查找频率

hash函数的构造方法

直接定址法

Hash[key]=a·key+b（a，b为常数）

优点：以关键字key的某个线性函数值为散列地址，不会发生冲突

缺点：要占用连续地址空间，空间效率低

除留余数法

Hash[key]=key mod p（p是一个整数）

设表长为m，取p≤m且p为质数

完整代码

#include <iostream>
#include "stdio.h"    
#include "stdlib.h"   
using namespace std;

#define HASHSIZE 12 // 定义散列表长度 
#define NULLKEY 0

//定义哈希表
typedef struct HashTable
{
	int *elem; // 数据元素存储地址，动态分配数组
	int count; //  当前数据元素个数
}HashTable;

int m = 0;

//初始化哈希表
int Init(HashTable* H)
{
	int i;
	m = HASHSIZE;
	H->elem = (int*)malloc(m * sizeof(int)); //分配内存
	H->count = m;
	for (i = 1; i <= m; i++)
	{
		H->elem[i] = NULLKEY;  //将哈希表的元素初始化为0
	}
	return 1;
}

//除留余数法
int Hash(int k)
{
	return k % (m+1);
}

//在哈希表中插入元素
void Insert(HashTable* H, int k)
{
	int addr = Hash(k);
	while (H->elem[addr] != NULLKEY)
	{
		addr = (addr + 1) % (m+1);//开放定址法
	}
	H->elem[addr] = k;
}
//在哈希表中查找元素
int Search(HashTable* H, int k)
{
	int addr = Hash(k); //求哈希地址

	while (H->elem[addr] != k)//开放定址法解决冲突
	{
		addr = (addr + 1) % (m+1);
		if (H->elem[addr] == NULLKEY || addr == Hash(k))
			return -1;
	}
	return addr;
}
//散列表元素显示
void Result(HashTable* H)
{
	int i;
	for (i = 1; i <= H->count; i++)
	{
		cout << H->elem[i] << "  ";
	}
	cout << endl;
}

void main()
{
	int i, j, addr;
	HashTable H;
	int arr[HASHSIZE] = { NULL };

	Init(&H);

	cout << "输入关键字集合：（"<<HASHSIZE<<"个）" << endl;
	for (i = 0; i < HASHSIZE; i++)
	{
		cin >> arr[i];
		Insert(&H, arr[i]);
	}
	cout << "存入哈希表中为：" << endl;
	Result(&H);

	cout << "输入要查找的元素：" << endl;
	cin >> j;
	addr = Search(&H, j);
	if (addr == -1)
		cout << "元素不存在！" << endl;
	else
		cout << j << "元素在表中的位置是：" << addr <<endl;

	system("pause");
	return;
}

开放地址法

有冲突时就去寻找下一个空的散列地址，只要表足够大，总能找到空的地址，并将元素存入

除留余数法：Hi=（Hash（key）+di）mod m
di为增量序列

链地址法

相同散列地址的记录链成一单链表，m个散列地址就设m个单链表，然后用一个数组将m个单链表的表头指针存储起来，形成一个动态的结构

优点：非同义词不会冲突，链表上空间动态申请，更适用于表长不确定的情况

查找效率分析

ASL取决于：散列函数、处理冲突的方法、散列表的装填因子

所以Hash表的查找效率既不是O(1),也不是O(n)

小结论

• 链地址法优于开地址法
• 除留余数法作散列函数优于其他类型函数

查找总结

顺序查找，折半查找，分块查找比较

	顺序查找	折半查找	分块查找
时间复杂度	O(n)	O(log^n)	与确定所在块的查找方法有关
特点	算法简单，对结构无要求，效率底	对表结构有要求，效率高	对结构有一定要求，效率介于顺序查找和折半查找之间
适用情况	任何结构的线性表，不经常做插入和删除	有序的顺序表，不经常做插入和删除	块间有序，块内无序的循序表，经常做插入和删除

折半查找和二叉排序树比较

	折半查找	二叉排序树
时间复杂度	O(log^n)	O(log^n)
特点	有序的顺序表，插入和删除需要移动大量元素	用二叉链表，插入和删除无需移动元素，只需修改指针
适用情况	不经常插入删除	经常插入和删除

哈希表:开地址法和链地址法比较

	开地址法	链地址法
空间	无指针域，存储效率高	附加指针域
时间复杂度	有二次聚集现象，查找效率低	无二次聚集现象，查找效率高
插入删除	不易实现	易于实现
适用情况	表的大小固定，适用于表长无变化	节点动态生成，适用于表长经常变化

---

图片来源：PDF整理笔记By: LI LIANGJI (Wechat:llj907015000)

本章完~