数据分析 | Logistic回归模型

一、Logistic回归模型

假定以下回归模型为：$z={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_p{x}_p$

则Logit变换为：
$$g(z)=\frac{1}{1+e^{-({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_p{x}_p)}}=h_{\beta }(X)$$
上式中的$h_{\beta }(X)$也被称为Logistic回归模型，它是将线性回归模型的预测值经过非线性的Logit函数转换为[0,1]之间的概率值。

Logit函数使得原本$z\in (-\infty ,+\infty )$的值，限制在$(0,1)$之间，从而进行概率分类。下图是Logit函数 $g(z)=\frac{1}{1+e^{-z}}$函数图像

​

01 模型变换

条件概率，y取值为1时的概率：$P(y=1|X;\beta )=h_{\beta }(X)=p$

条件概率，y取值为0时的概率：$P(y=0|X;\beta )=1-h_{\beta }(X)=1-p$

则两个概率的商为：
$$\frac{p}{1-p}=\frac{h_{\beta }(X)}{1-h_{\beta }(X)}=e^{{\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_p{x}_p}$$

02 参数求解过程

对于上述两个条件概率式子，我们可以等价于：
$$P(y|X;\beta )=h_{\beta }(X{)}^y\times (1-h_{\beta }(X){)}^{1-y},(y=1,0)$$
构造似然函数：
$$L(\beta )=\prod _{i=1}^n{h}_{\beta }(x^i{)}^{y^i}\times (1-h_{\beta }(x^i){)}^{1-y^i}$$
似然函数对数化：
$$l(\beta )=log(L(\beta ))=\sum _{i=1}^n(y^{i}log(h_{\beta }{x}^i))+(1-y^i)log(1-h_{\beta }{x}^i)$$
由于直接求导函数为0无法构建完整的方程组，考虑梯度下降：
$$J(\beta )=-l(\beta )=-\sum _{i=1}^n(y^{i}log(h_{\beta }{x}^i)+(1-y^i)log(1-h_{\beta }{x}^i))$$
于是，对每一个未知数${\beta }_j$做梯度下降：
$${\beta }_j:={\beta }_j-\alpha \frac{\partial J(\beta )}{\partial {\beta }_j}$$
其中，alpha为学习率，也成为参数beta变化的步长，通常可取0.1、0.05、0.01等，设置的$\alpha$不可过小也不可过大。

03 参数含义的解释

以癌症为例，假设影响是否得癌症的因素有性别$({\beta }_1)$和肿瘤体积$({\beta }_2)$两个变量，则Logistic模型可以按照事件发生比的形式改写为：
$$odds=\frac{p}{1-p}=e^{{\beta }_0+{\beta }_{1}Gender+{\beta }_{2}Volumn}$$
分别以性别变量和肿瘤体积变量为例，解释系数${\beta }_1和{\beta }_2$的含义。假设性别中男用1表示，女用0表示。则：
$$\frac{odd{s}_1}{odd{s}_0}=\frac{e^{{\beta }_0}\times e^{{\beta }_1\times 1}\times e^{{\beta }_{2}Volumn}}{e^{{\beta }_0}\times e^{{\beta }_1\times 0}\times e^{{\beta }_{2}Volumn}}=e^{{\beta }_1}$$
所以，性别变量的发生比率为$e^{{\beta }_1}$，表示男性患癌的发生比约为女性患癌发生比的$e^{\beta 1}$倍

对于连续型自变量而言，假设肿瘤体积为$Volum{n}_0$，当肿瘤体积增加1个单位时，体积为$Volum{n}_0+1$，则：
$$\frac{odd{s}_{Volum{n}_0+1}}{odd{s}_{Volum{n}_0}}=\frac{e^{{\beta }_0}\times e^{{\beta }_{1}Gender}\times e^{{\beta }_2(Volum{n}_0+1)}}{e^{{\beta }_0}\times e^{{\beta }_{1}Gender}\times e^{{\beta }_2(Volum{n}_0)}}=e^{{\beta }_2}$$
所以，在其他变量不变的情况下，肿瘤体积每增加一个单位，将会使患癌发生比变化$e^{{\beta }_2}$倍。

二、模型评估

01 混淆矩阵

混淆矩阵的每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目；每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目。

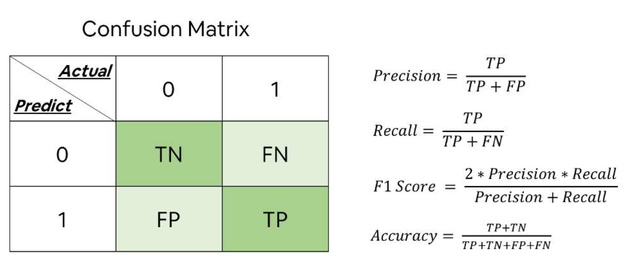
其中：
$$\begin{gathered} 正例覆盖率：Sensitivity=\frac{TP}{TP+FN} \\ 负例覆盖率：Specificity=\frac{TN}{TN+FP} \end{gathered}$$

02 ROC曲线

受试者工作特征曲线 （receiver operating characteristic curve，简称ROC曲线），又称为感受性曲线（sensitivity curve）

在不使用模型的情况下，Sensitivity 和1-Specificity之比恒为1，上图蓝色曲线以下面积称为AUC，当AUC在0.8以上时，模型就可以接受了。

三、代码实现

01 sklearn包

LogisticRegression(tol=0.0001, fit_intercept=True, class_weight=None, max_iter=100)

• tol：用于指定模型收敛的阈值
• fit_intercept：是否拟合模型的截距项，默认为True
• class_weight：用于指定因变量类别的权重，若为字典，则通过字典的形式{class_label:weight}传递每个类别的权重，若为字符串“balanced”，则每个分类的权重与实际样本中的比例成反比，当各分类存在严重不平衡时，设置为"balanced"较好；若为None，则表示每个分类的权重相等
• max_iter：指定模型求解过程中的最大迭代次数，默认为100

# 导入第三方模块
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn import linear_model

# 读取数据
sports = pd.read_csv(r'Run or Walk.csv')
# 提取出所有自变量名称
predictors = sports.columns[4:]
# 构建自变量矩阵
X = sports.ix[:,predictors]
# 提取y变量值
y = sports.activity
# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234)

# 利用训练集建模
sklearn_logistic = linear_model.LogisticRegression()
sklearn_logistic.fit(X_train, y_train)
# 返回模型的各个参数
print(sklearn_logistic.intercept_, sklearn_logistic.coef_)

结果为：

[ 4.35613952] [[ 0.48533325  6.86221041 -2.44611637 -0.01344578 -0.1607943   0.13360777]]

其中第一个为截距项，后边为各变量对应的偏回归系数。

# 模型预测
sklearn_predict = sklearn_logistic.predict(X_test)
# 预测结果统计
pd.Series(sklearn_predict).value_counts()

下面进行模型评估：

# 导入第三方模块
from sklearn import metrics
# 混淆矩阵
cm = metrics.confusion_matrix(y_test, sklearn_predict, labels = [0,1])
cm

结果为：

array([[9971, 1120],
       [2150, 8906]], dtype=int64)

计算Accuracy、Sensitivity、Specificity

Accuracy = metrics.scorer.accuracy_score(y_test, sklearn_predict)
Sensitivity = metrics.scorer.recall_score(y_test, sklearn_predict)
Specificity = metrics.scorer.recall_score(y_test, sklearn_predict, pos_label=0)
print('模型准确率为%.2f%%:' %(Accuracy*100))
print('正例覆盖率为%.2f%%' %(Sensitivity*100))
print('负例覆盖率为%.2f%%' %(Specificity*100))

结果为：

模型准确率为85.24%:
正例覆盖率为80.55%
负例覆盖率为89.90%

02 statsmodels.api包

# -----------------------第一步 建模 ----------------------- #
# 导入第三方模块
import statsmodels.api as sm
import pandas as pd
import numpy as np
from sklearn import metrics
from sklearn import model_selection
from sklearn import linear_model

# 读取数据
sports = pd.read_csv(r'Run or Walk.csv')
# 提取出所有自变量名称
predictors = sports.columns[4:]
# 构建自变量矩阵
X = sports.ix[:,predictors]
# 提取y变量值
y = sports.activity
# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234)
# 为训练集和测试集的X矩阵添加常数列1
X_train2 = sm.add_constant(X_train)
X_test2 = sm.add_constant(X_test)
# 拟合Logistic模型
sm_logistic = sm.Logit(y_train, X_train2).fit()
# 返回模型的参数
sm_logistic.params

# -----------------------第二步 预测构建混淆矩阵 ----------------------- #
# 模型在测试集上的预测
sm_y_probability = sm_logistic.predict(X_test2)
# 根据概率值，将观测进行分类，以0.5作为阈值
sm_pred_y = np.where(sm_y_probability >= 0.5, 1, 0)
# 混淆矩阵
cm = metrics.confusion_matrix(y_test, sm_pred_y, labels = [0,1])
cm

# -----------------------第三步 绘制ROC曲线 ----------------------- #
import matplotlib.pyplot as plt
# 计算真正率和假正率 
fpr,tpr,threshold = metrics.roc_curve(y_test, sm_y_probability)
# 计算auc的值  
roc_auc = metrics.auc(fpr,tpr)
# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()