数据分析 | KNN模型

一、模型思想

邻近算法，或者说K最邻近（KNN，K-NearestNeighbor）分类算法是数据挖掘分类技术中最简单的方法之一。

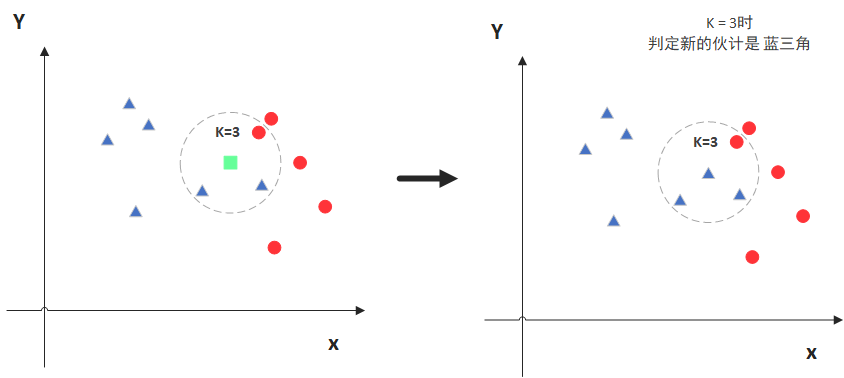
如上图所示，模型的本质就是寻找k个最近的样本，然后基于最近样本做“预测”。对于离散型因变量来说，从k个最近的已知类别样本中挑选出频率最高的类别用于未知样本的判断；对于连续变量来说，则是将k个最近的已知样本均值作为未知样本的预测。

模型的执行步骤如下：

1. 确定未知样本近邻的个数k值
2. 根据某种度量样本间相似度的指标，将每一个未知类别样本的最近k个已知样本搜寻出来，形成簇
3. 对搜寻出来的已知样本进行投票，将各簇下类别最多的分类用作未知样本点的预测

二、k值的选择

不同的k值对模型的预测准确性会有较大的影响，若k值过于偏小，可能会导致模型的过拟合；若k值偏大，又可能会使模型欠拟合。

01 设置权重

若k值设置的比较大时，担心模型发生欠拟合的现象时，可以设置近邻样本的投票权重，若已知样本距离未知样本比较远时，则对应的权重就设置得小一点，否则权重就大一点，通常可以将权重设置为距离的倒数。

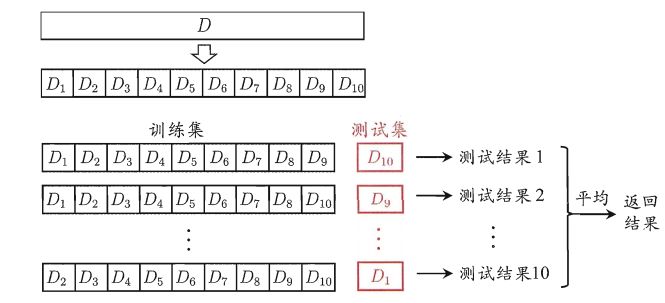
02 交叉验证

采用多重交叉验证法，就是将k取不同的值，然后在每种值下执行m重交叉验证，最后选出平均误差最小的k值

三、距离度量

01 欧式距离

在n维空间中，对于两点 $A(x_1,x_2,\cdots ,x_n)$ 和 $B(x_1,x_2,\cdots ,x_n)$ 间距离为：
$$d_{A,B}=\sqrt{(y_1-x_1{)}^2+(y_2-x_2{)}^2+\cdots +(y_n-x_n{)}^2}$$

02 曼哈顿距离

我们可以定义曼哈顿距离的正式意义为L1-距离或城市区块距离，也就是在欧几里德空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。

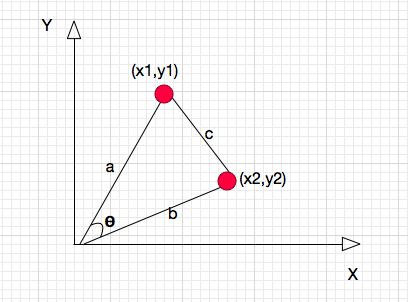
在平面上，坐标(x1,y1)的i点与坐标(x2,y2)的j点的曼哈顿距离为：
$$d_{ij}=|x_1-x_2|+|y_1-y_2|$$
以此延伸，在n维空间中，对于两点 $A(x_1,x_2,\cdots ,x_n)$ 和 $B(x_1,x_2,\cdots ,x_n)$ 间的曼哈顿距离为：
$$d_{A,B}=|y_1-x_1|+|y_2-x_2|+\cdots +|y_n-x_n|$$
要注意的是，曼哈顿距离依赖坐标系统的转度，而非系统在坐标轴上的平移或映射。

03 余弦相似度

余弦相似度，又称为余弦相似性，是通过计算两个向量的夹角余弦值来评估他们的相似度。余弦相似度将向量根据坐标值，绘制到向量空间中，如最常见的二维空间。

此时，二维空间AB两点的余弦相似度为：
$$Similarit{y}_{A,B}=Cos\theta =\frac{x_1{x}_2+y_1{y}_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}}$$
同理，在n为空间的AB两点，其余弦相似度为:
$$Similarit{y}_{A,B}=Cos\theta =\frac{\overrightarrow{A}\cdot \overrightarrow{B}}{|\overrightarrow{A}||\overrightarrow{B}|}$$

四、代码实现

neighbors.KNeighborsClassfier(n_neighbors=5, weights='uniform', p=2, metric='minkowski')

• n_neighbors：指定临近样本个数k，默认为5个
• weights：指定临近样本的投票权重，默认为uniform，表示所权重一样；若为“distance”，则表示投票权重与距离成反比。
• metric：指定距离的度量指标，默认为闵可夫斯基距离
• p：当参数metric为闵可夫斯基距离时，p=1，表示计算点之间的曼哈顿距离；p=2，表示计算点之间的欧氏距离；默认为2

# 导入第三方包
import pandas as pd
# 导入数据
Knowledge = pd.read_excel(r'Knowledge.xlsx')
# 返回前5行数据
Knowledge.head()

	STG	SCG	STR	LPR	PEG	UNS
0	0.00	0.00	0.00	0.00	0.00	Very Low
1	0.08	0.08	0.10	0.24	0.90	High
2	0.06	0.06	0.05	0.25	0.33	Low
3	0.10	0.10	0.15	0.65	0.30	Middle
4	0.08	0.08	0.08	0.98	0.24	Low

# 构造训练集和测试集
# 导入第三方模块
from sklearn import model_selection
# 将数据集拆分为训练集和测试集
predictors = Knowledge.columns[:-1]
X_train, X_test, y_train, y_test = model_selection.train_test_split(Knowledge[predictors], Knowledge.UNS, 
                                                                    test_size = 0.25, random_state = 1234)

# 导入第三方模块
import numpy as np
from sklearn import neighbors
import matplotlib.pyplot as plt

# 设置待测试的不同k值
K = np.arange(1,np.ceil(np.log2(Knowledge.shape[0]))).astype(int)
# 构建空的列表，用于存储平均准确率
accuracy = []
for k in K:
    # 使用10重交叉验证的方法，比对每一个k值下KNN模型的预测准确率
    cv_result = model_selection.cross_val_score(neighbors.KNeighborsClassifier(n_neighbors = k, weights = 'distance'), 
                                                X_train, y_train, cv = 10, scoring='accuracy')
    accuracy.append(cv_result.mean())

# 从k个平均准确率中挑选出最大值所对应的下标    
arg_max = np.array(accuracy).argmax()
# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 绘制不同K值与平均预测准确率之间的折线图
plt.plot(K, accuracy)
# 添加点图
plt.scatter(K, accuracy)
# 添加文字说明
plt.text(K[arg_max], accuracy[arg_max], '最佳k值为%s' %int(K[arg_max]))
# 显示图形
plt.show()

此时，通过图像得到最佳k值

# 导入第三方模块
from sklearn import metrics

# 重新构建模型，并将最佳的近邻个数设置为6
knn_class = neighbors.KNeighborsClassifier(n_neighbors = 6, weights = 'distance')
# 模型拟合
knn_class.fit(X_train, y_train)
# 模型在测试数据集上的预测
predict = knn_class.predict(X_test)
# 构建混淆矩阵
cm = pd.crosstab(predict,y_test)
cm

获得混淆矩阵
UNS	High	Low	Middle	Very Low
row_0				
High	29	0	0	0
Low	0	34	3	5
Middle	1	0	23	0
Very Low	0	0	0	6

# 分类模型的评估报告
print(metrics.classification_report(y_test, predict))

 precision    recall  f1-score   support

       High       1.00      0.97      0.98        30
        Low       0.81      1.00      0.89        34
     Middle       0.96      0.88      0.92        26
   Very Low       1.00      0.55      0.71        11

avg / total       0.93      0.91      0.91       101