实验一 信号的时域描述与运算
一、实验目的
- 掌握信号的MATLAB表示及其可视化方法
- 掌握信号基本时域运算的MATLAB实现方法
- 利用MATLAB分析常用信号,加深对信号时域特性的理解
二、实验原理
- 连续时间信号的MATLAB表示
- 连续时间信号的时域运算
- 离散时间信号的MATLAB表示
- 离散时间信号的时域运算
三、实验内容
(1)
利用MATLAB绘制下列连续时间信号波形:
(1)_1
x ( t ) = ( 1 − e − 0.5 t ) u ( t ) x(t) = (1 - {e^{ - 0.5t}})u(t) x(t)=(1−e−0.5t)u(t)
实现代码如下:
clc
t = -10:0.01:10;
x = (1-exp(-0.5*t)).*heaviside(t);
plot(t,x)
画出图形如下:

(1)_2
x ( t ) = cos ( π t ) [ u ( t ) − u ( t − 2 ) ] x(t) = \cos (\pi t)[u(t) - u(t - 2)] x(t)=cos(πt)[u(t)−u(t−2)]
实现代码如下:
clc
t = -10:0.01:10;
x = cos(pi*t).*(heaviside(t)-heaviside(t-2));
plot(t,x)
画出图像如下:

(1)_3
x ( t ) = ∣ t ∣ 2 cos ( π t ) [ u ( t + 2 ) − u ( t − 2 ) ] x(t) = \frac{{\left| t \right|}}{2}\cos (\pi t)[u(t + 2) - u(t - 2)] x(t)=2∣t∣cos(πt)[u(t+2)−u(t−2)]
实现代码如下:
clc
t = -10:0.01:10;
x = 0.5*abs(t).*cos(pi*t).*(heaviside(t+2)-heaviside(t-2));
plot(t,x)
画出图像如下:

(1)_4
x ( t ) = e − t sin ( 2 π t ) [ u ( t ) − u ( t − 3 ) ] x(t) = {e^{ - t}}\sin (2\pi t)[u(t) - u(t - 3)] x(t)=e−tsin(2πt)[u(t)−u(t−3)]
实现代码如下:
clc
t = -10:0.01:10;
x = exp(-t).*sin(pi*2*t).*(heaviside(t)-heaviside(t-3));
plot(t,x)
画出图像如下:

(2)
利用MATLAB绘制下列连续时间信号波形
(2)_1
x ( n ) = u ( n − 3 ) x(n) = u(n - 3) x(n)=u(n−3)
实现代码如下:
clc
n = -10:10;
x = heaviside(n-3);
stem(n,x,"filled")
xlabel('n')
title('x(n)')
画出图像如下:

(2)_2
x ( n ) = ( − 1 / 2 ) n u ( n ) x(n) = {( - 1/2)^n}u(n) x(n)=(−1/2)nu(n)
实现代码如下:
clc
n = -10:10;
x = heaviside(n).*(-0.5).^n;
stem(n,x,"filled")
xlabel('n')
title('x(n)')
画出图像如下:

(2)_3
x ( n ) = n [ u ( n ) − u ( n − 5 ) ] x(n) = n[u(n) - u(n - 5)] x(n)=n[u(n)−u(n−5)]
实现代码如下:
clc
n = -10:10;
x = n.*(heaviside(n)-heaviside(n-5));
stem(n,x,"filled")
xlabel('n')
title('x(n)')
画出图像如下:

(2)_4
x ( n ) = sin ( n π / 2 ) u ( n ) x(n) = \sin (n\pi /2)u(n) x(n)=sin(nπ/2)u(n)
实现代码如下:
clc
n = -10:10;
x = sin(n*pi*0.5).*heaviside(n);
stem(n,x,"filled")
xlabel('n')
title('x(n)')
画出图像如下:
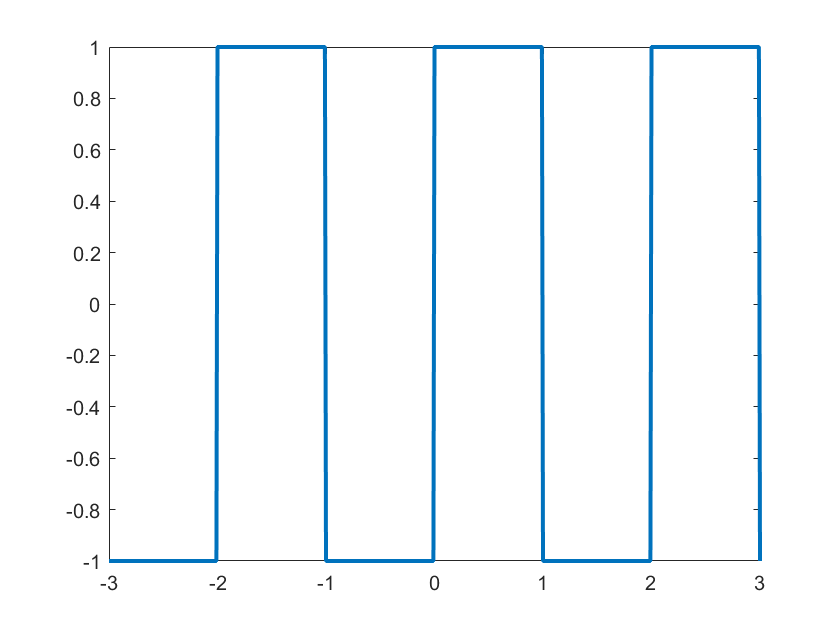
(3)
利用MATLAB生成并绘制连续周期矩形波信号,要求周期为2,峰值为3,显示三个周期的波形。
实现代码如下:
t = -3:0.01:3;
x = square(2*pi.*t/2);
plot(t,x,'LineWidth', 2)
绘制图像如下:
(4)
已知如下图所示信号x1(t),及信号x2(t)=sin(2 π \pi πt),用MATLAB绘出下列信号的波形:

(4)_1
x 3 ( t ) = x 1 ( t ) + x 2 ( t ) {x_3}(t) = {x_1}(t) + {x_2}(t) x3(t)=x1(t)+x2(t)
实现代码如下:
t = -10:0.01:10;
x1 = rectpuls(t-2,4).*(4-t);
x2 = sin(2*pi*t);
x3 = x1+x2;
plot(t,x3,'LineWidth', 2)
绘制图像如下:

(4)_2
x 4 ( t ) = x 1 ( t ) × x 2 ( t ) {x_4}(t) = {x_1}(t) \times {x_2}(t) x4(t)=x1(t)×x2(t)
实现代码如下:
t = -10:0.01:10;
x1 = rectpuls(t-2,4).*(4-t);
x2 = sin(2*pi*t);
x4 = x1.*x2;
plot(t,x4,'LineWidth', 2)
绘制图像如下:

(4)_3
x 5 ( t ) = x 1 ( − t ) + x 1 ( t ) {x_5}(t) = {x_1}( - t) + {x_1}(t) x5(t)=x1(−t)+x1(t)
实现代码如下:
clc
t = -10:0.01:10;
x1 = rectpuls(t-2,4).*(4-t);
x2 = sin(2*pi*t);
t_shifted = -t;
x1_shifted = interp1(t, x1, t_shifted);
x5 = x1 + x1_shifted;
plot(t,x5,'LineWidth', 2)
绘制图像如下:

(4)_4
x 6 ( t ) = x 2 ( t ) × x 3 ( t − 1 ) {x_6}(t) = {x_2}(t) \times {x_3}(t - 1) x6(t)=x2(t)×x3(t−1)
实现代码如下:
clc
t = -10:0.01:10;
x1 = rectpuls(t-2,4).*(4-t);
x2 = sin(2*pi*t);
x3 = x1+x2;
t_shifted = t - 1;
x3_shifted = interp1(t, x3, t_shifted);
x5 = x2.*x3_shifted;
plot(t,x5,'LineWidth', 2)
绘制图像如下:
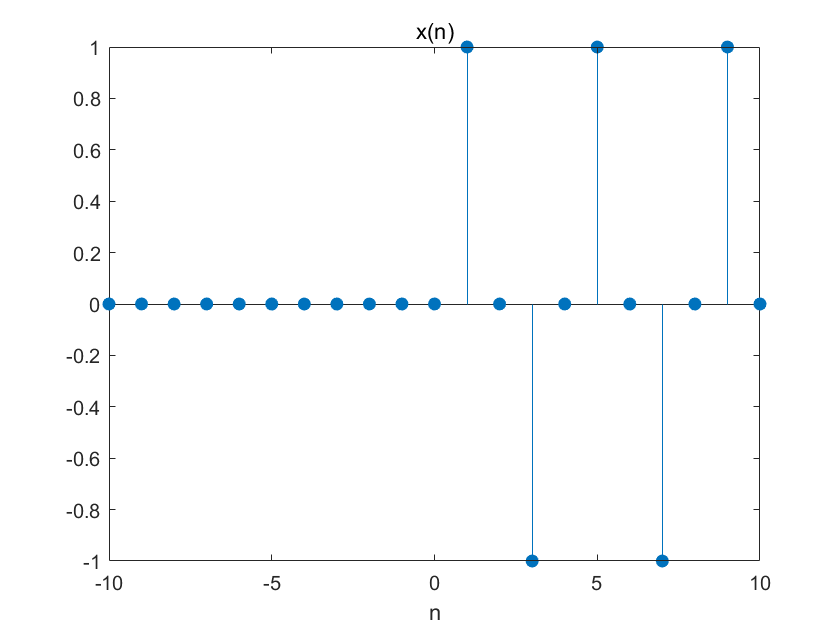
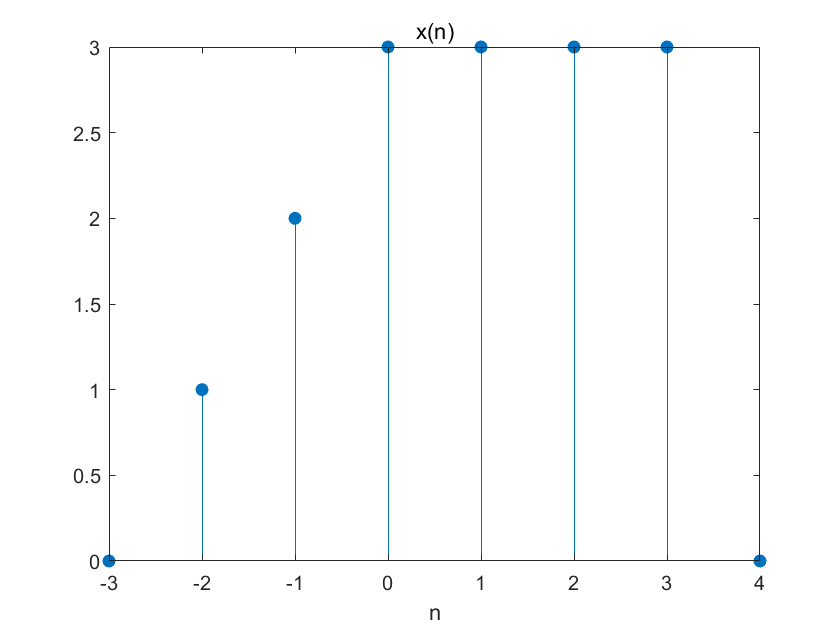
(5)
已知离散时间信号x(n)波形如下图所示,用MATLAB绘出x(n)、x(-n)、x(n+2)和x(n-2)的波形。

实现代码如下:
clc
figure(1)
n = -3:4;
x = [0 1 2 3 3 3 3 0];
stem(n,x,"filled")
xlabel('n')
title('x(n)')
figure(2)
n1 = -n;
stem(n1,x,"filled")
xlabel('n')
title('x(-n)')
figure(3)
n2 = n-2;
stem(n2,x,"filled")
xlabel('n')
title('x(n+2)')
figure(4)
n3 = n+2;
stem(n3,x,"filled")
xlabel('n')
title('x(n-2)')
绘制图像如下:
|

|

|

|
(6)
用MATLAB编程绘制下列信号的时域波形,观察信号是否为周期信号?若是周期信号,周期是多少?若不是周期信号,请说明原因。
(6)_1
x ( t ) = 1 + cos ( π 4 t − π 3 ) + 2 cos ( π 2 t − π 4 ) + cos ( 2 π t ) x(t) = 1 + \cos \left( {\frac{\pi }{4}t - \frac{\pi }{3}} \right) + 2\cos \left( {\frac{\pi }{2}t - \frac{\pi }{4}} \right) + \cos (2\pi t) x(t)=1+cos(4πt−3π)+2cos(2πt−4π)+cos(2πt)
实现代码如下:
clc
t = -10:0.01:10;
x = 1+cos(0.25*pi*t-pi/3)+2*cos(pi/2*t-pi/4)+cos(2*pi*t);
plot(t,x)
绘制图像如下:

它是一个周期信号,周期为8
(6)_2
x ( t ) = sin ( t ) + 2 sin ( π t ) x(t) = \sin (t) + 2\sin (\pi t) x(t)=sin(t)+2sin(πt)
实现代码如下:
clc
t = -10:0.01:10;
x = sin(t)+2*sin(pi*t);
plot(t,x)
绘制图像如下:
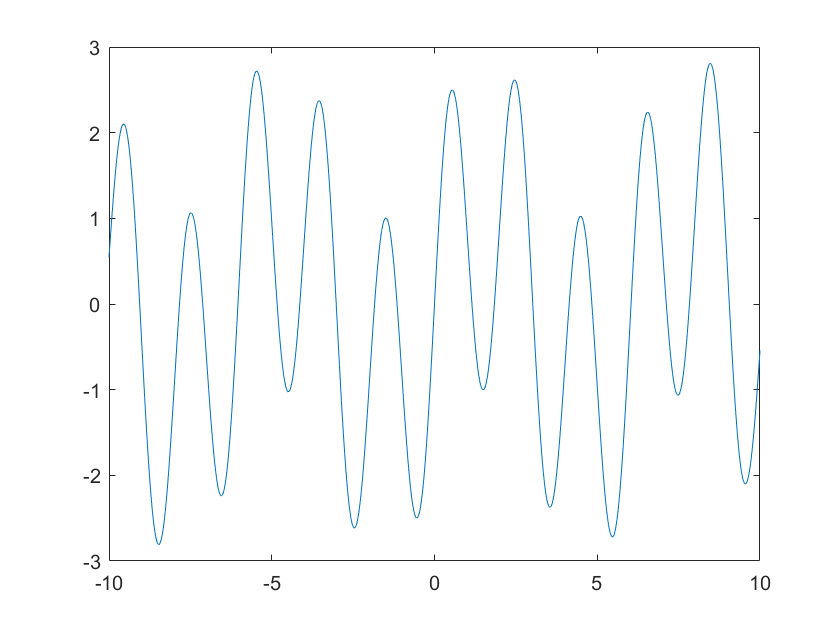
它不是一个周期信号,因为组成它的两个三角函数的周期比值不是一个有理数
(6)_3
x ( n ) = 2 + 3 sin ( 2 n π 3 − π 8 ) x(n) = 2 + 3\sin \left( {\frac{{2n\pi }}{3} - \frac{\pi }{8}} \right) x(n)=2+3sin(32nπ−8π)
实现代码如下:
clc
n = -10:10;
x = 2+3*sin(2*n*pi/3-pi/8);
stem(n,x,"filled")
xlabel('n')
title('x(n)')
绘制图像如下:

它是一个周期信号,周期为3
(6)_4
x ( n ) = cos ( n π 6 ) + sin ( n π 3 ) + cos ( n π 2 ) x(n) = \cos \left( {\frac{{n\pi }}{6}} \right) + \sin \left( {\frac{{n\pi }}{3}} \right) + \cos \left( {\frac{{n\pi }}{2}} \right) x(n)=cos(6nπ)+sin(3nπ)+cos(2nπ)
实现代码如下:
clc
n = -10:10;
x = cos(n*pi/6)+sin(n*pi/3)+cos(n*pi/2);
stem(n,x,"filled")
xlabel('n')
title('x(n)')
绘制图像如下:

它是一个周期信号,周期为12
四、心得体会
本次实验考察了使用MATLAB绘图,在绘图过程中应注意连续信号与离散信号的区别。
实验二 LTI系统的时域分析
一、实验目的
- 掌握利用MATLAB对系统进行时城分析的方法
- 掌握连续时间系统零状态响应、冲激响应和阶跃响应的求解方法
- 掌握求解离散时间系统响应、单位抽样响应的方法。
- 加深对卷积积分和卷积和的理解。掌握利用计算机进行卷积积分和卷积和计算的方法。
二、实验原理
- 连续时间系统时域分析的MATLAB实现
- 离散时间系统时域分析的MATLAB实现
- 卷积与卷积积分
三、实验内容
(1)
已知描述模拟低通、高通、带通和带阻滤波器的微分方程如下,试采用MATLAB绘出各系统的单位冲激响应和单位阶跃响应波形。
(1)_1
y ′ ′ ( t ) + 2 y ′ ( t ) + y ( t ) = x ( t ) y''(t) + \sqrt 2 y'(t) + y(t) = x(t) y′′(t)+2y′(t)+y(t)=x(t)
实现代码如下:
clc
a = [1 sqrt(2) 1];
b = [1];
sys = tf(b,a);
figure(1)
impulse(sys)
figure(2)
step(sys)
绘出图像如下:

|

|
(1)_2
y ′ ′ ( t ) + 2 y ′ ( t ) + y ( t ) = x ′ ′ ( t ) y''(t) + \sqrt 2 y'(t) + y(t) = x''(t) y′′(t)+2y′(t)+y(t)=x′′(t)
实现代码如下:
clc
a = [1 sqrt(2) 1];
b = [1 0 0];
sys = tf(b,a);
figure(1)
impulse(sys)
figure(2)
step(sys)
绘制图像如下:
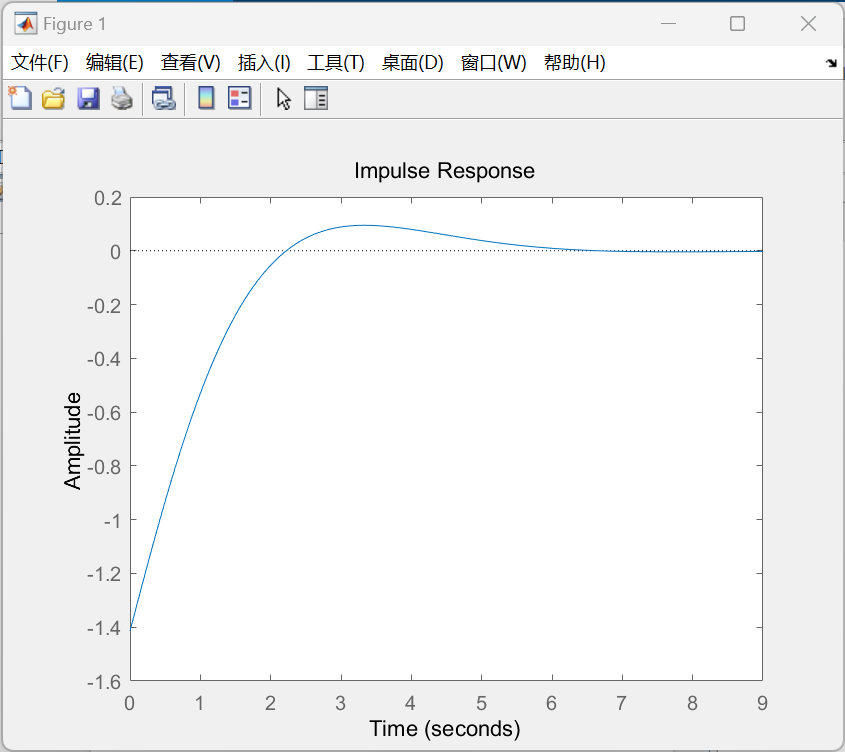
|

|
(1)_3
y ′ ′ ( t ) + y ′ ( t ) + y ( t ) = x ′ ( t ) y''(t) + y'(t) + y(t) = x'(t) y′′(t)+y′(t)+y(t)=x′(t)
实现代码如下:
clc
a = [1 1 1];
b = [1 0];
sys = tf(b,a);
figure(1)
impulse(sys)
figure(2)
step(sys)
绘制图像如下:

|

|
(1)_4
y ′ ′ ( t ) + y ′ ( t ) + y ( t ) = x ′ ′ ( t ) + x ( t ) y''(t) + y'(t) + y(t) = x''(t) + x(t) y′′(t)+y′(t)+y(t)=x′′(t)+x(t)
实现代码如下:
clc
a = [1 1 1];
b = [1 0 1];
sys = tf(b,a);
figure(1)
impulse(sys)
figure(2)
step(sys)
绘制图像如下:

|

|
(2)
已知某系统可以由如下微分方程描述
y
′
′
(
t
)
+
y
′
(
t
)
+
6
y
(
t
)
=
x
(
t
)
y''(t) + y'(t) + 6y(t) = x(t)
y′′(t)+y′(t)+6y(t)=x(t)
(2)_1
请利用MATLAB绘出该系统冲激响应和阶跃响应的时域波形
实现代码如下:
clc
a = [1 1 6];
b = [1];
sys = tf(b,a);
figure(1)
impulse(sys)
figure(2)
step(sys)
绘出图像如下:

|

|
(2)_2
根据冲激响应的时域波形分析系统的稳定性
根据冲激响应的时域波形,它在有限的时间内收敛到零,说明系统是稳定的。
(2)_3
如果系统的输人为x(t)=e-tu(t),求系统的零状态响应
实现代码如下:
clc
a = [1 1 6];
b = [1];
sys = tf(b,a);
t = 0:0.01:10;
x = exp(-t).*heaviside(t);
lsim(sys,x,t)
绘出图像如下:

(3)
已知描述离散系统的微分方程如下,试采用MATLAB绘出各系统的单位抽样响应,并根据单位抽样响应的时域波形分析系统的稳定性。
(3)_1
y ( n ) + 3 y ( n − 1 ) + 2 y ( n − 2 ) = x ( n ) y(n) + 3y(n - 1) + 2y(n - 2) = x(n) y(n)+3y(n−1)+2y(n−2)=x(n)
实现代码如下:
clc
a = [1 3 2];
b = [1];
y = impz(b,a);
n = 0:length(y)-1;
stem(n,y,'filled');
xlabel('n');
title('y(n)');
绘制图像如下:

(3)_2
y ( n ) + 3 y ( n − 1 ) + 2 y ( n − 2 ) = x ( n ) y(n) + 3y(n - 1) + 2y(n - 2) = x(n) y(n)+3y(n−1)+2y(n−2)=x(n)
实现代码如下:
clc
a = [1 -0.5 0.8];
b = [1 -3];
y = impz(b,a);
n = 0:length(y)-1;
stem(n,y,'filled');
xlabel('n');
title('y(n)');
绘制图像如下:

(4)
已知系统可以由如下差分方程描述
y
(
n
)
+
3
y
(
n
−
1
)
+
0.25
y
(
n
−
2
)
=
x
(
n
)
y(n) + 3y(n - 1) + 0.25y(n - 2) = x(n)
y(n)+3y(n−1)+0.25y(n−2)=x(n)
试采用MATLAB绘出该系统的单位抽样响应波形和单位阶跃响应波形。
实现代码如下:
clc
a = [1 1 0.5];
b = [1];
figure(1)
y = impz(b,a);
n = 0:length(y)-1;
figure(1)
stem(n,y,'filled');
xlabel('n');
title('单位抽样响应');
gn=dstep(b,a,n+1);
figure(2)
stem(n,gn,'filled');
title('单位阶跃响应');
xlabel('n');
绘制图像如下:

|

|
(5)
采用MATLAB计算如下两个序列的卷积,并绘出图形
x
1
(
n
)
=
{
1
,
2
,
1
,
1
}
x
2
(
n
)
=
{
1
,
−
2
⩽
n
⩽
20
,
e
l
s
e
}
{x_1}(n) = \{ 1,2,1,1\} {x_2}(n) = \left\{ \begin{gathered} 1, - 2 \leqslant n \leqslant 2 0,else \end{gathered} \right\}
x1(n)={1,2,1,1}x2(n)={1,−2⩽n⩽20,else}
实现代码如下:
clc
n1 = -1:2;
l1 = 2+1+1;
x1 = [1 2 1 1];
n2 = -2:2;
x2 = [1 1 1 1 1];
l2 = 2+2+1;
x = conv(x1,x2);
l = l1+l2-1;
n = (-1-2):(l-1-2-1);
stem(n,x,'filled')
绘制图像如下:

(6)
已知某LTI离散系统其单位抽样响应 h ( n ) = s i n ( 0.5 n ) , n ⩾ 0 h\left( n \right) = sin\left( {0.5n} \right),n \geqslant 0 h(n)=sin(0.5n),n⩾0,系统的输人为 x ( n ) = sin ( 0.2 n ) , n ⩾ 0 x(n) = \sin (0.2n),n \geqslant 0 x(n)=sin(0.2n),n⩾0,计算当n=0,1,2,…,40时系统的零状态响应y(n),绘出x(n),h(n)和y(n)时域波形
实现代码如下:
clc
n = 0:40;
h = sin(0.5*n);
x = sin(0.2*n);
y = conv(h,x);
n1 = 0:(40+40);
figure(1)
stem(n,x,"filled")
title('x(n)')
figure(2)
stem(n,h,"filled")
title('h(n)')
figure(3)
stem(n1,y,'filled')
title('y(n)')
绘出图像如下:

|

|

|
(7)
已知两个连续时间信号如下图所示,试采用MATLAB求这两个信号的卷积。

编写的连续信号求卷积函数如下:
function [x,t] = sconv(x1,x2,t1,t2,dt)
x = conv(x1,x2);
x = x*dt;
t0 = t1(1)+t2(1);
l = length(x1)+length(x2)-2;
t = t0:dt:(t0+l*dt);
end
编写的求卷积脚本程序如下:
clc
dt = 0.01;
t1 = -1:dt:1;
x1 = 2*rectpuls(t1,2);
t2 = -2:dt:2;
x2 = rectpuls(t2,4);
[x,t] = sconv(x1,x2,t1,t2,dt);
plot(t,x);
xlabel('t');
title('x(t)=x_1(t)*x_2(t)')
绘制图像如下:
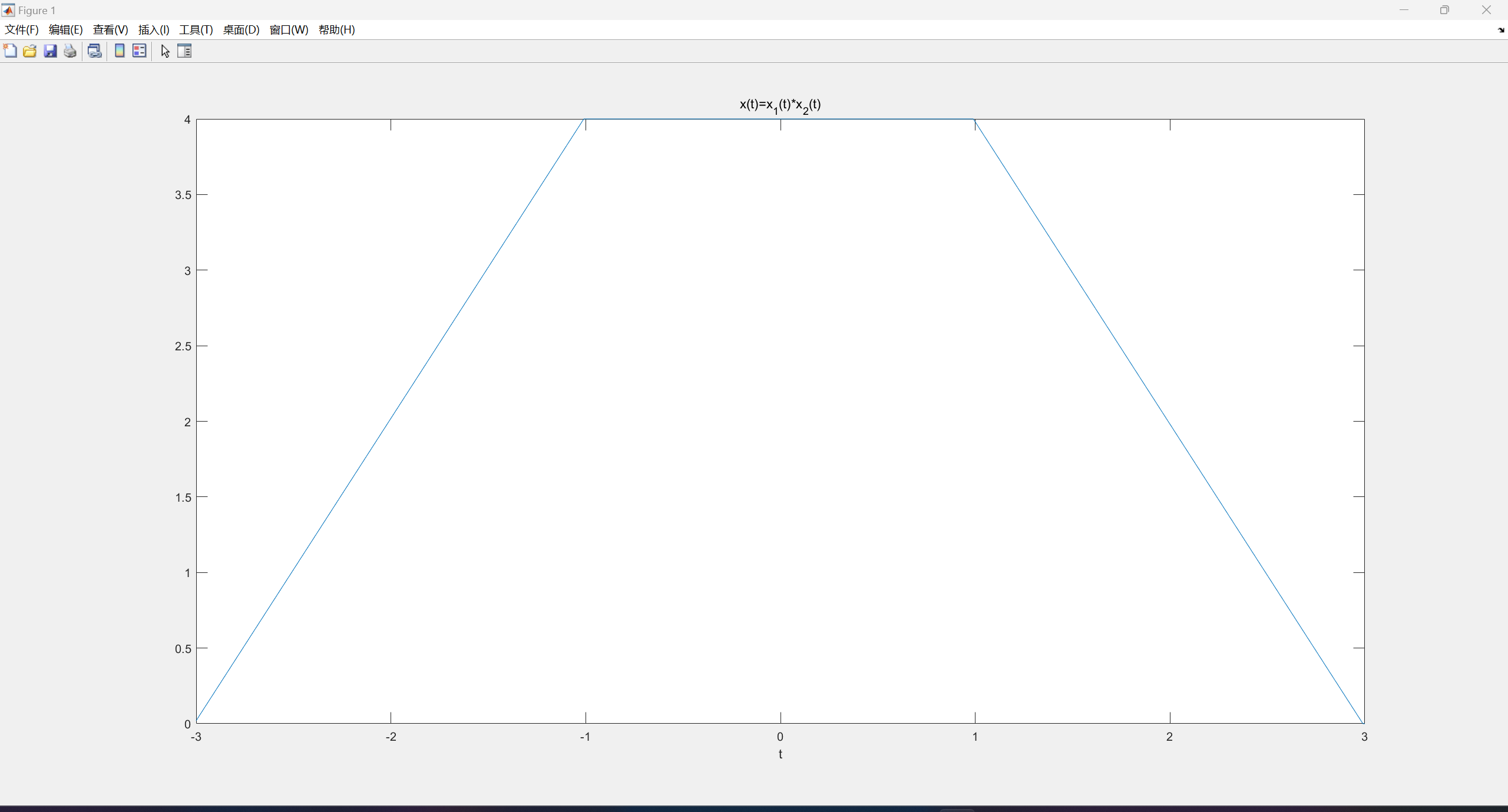
四、心得体会
通过这次实验,我更加深入地了解了信号与系统中LTI系统的时域分析方法,并且深刻体会到了实践操作的重要性。这些知识和经验也将对我未来的学习和研究产生深远影响。
实验三 信号的频域分析
一、实验目的
- 深入理解信号频谱的概念,掌握信号的频域分析方法。
- 观察典型周期信号和非周期信号的频谱,掌握其频谱特性。
二、实验原理
- 连续周期时间信号的频谱分析
- 连续非周期时间信号的频谱分析
- 离散周期时间信号的频域分析
- 离散非周期时间信号的频域分析
三、实验内容
(1)
已知x(t)是如下图所示的周期矩形脉冲信号

-
计算该信号的傅里叶级数
已知狄里赫利条件:
x ( t ) = ∑ k = − ∞ + ∞ c k e j k w 0 t c k = 1 T 0 ∫ T 0 x ( t ) e − j k w 0 t d t x(t) = \sum\limits_{k = - \infty }^{ + \infty } {{c_k}{e^{jk{w_0}t}}} {c_k} = \frac{1}{{{T_0}}}\int_{{T_0}} {x(t){e^{ - jk{w_0}t}}dt} x(t)=k=−∞∑+∞ckejkw0tck=T01∫T0x(t)e−jkw0tdt
T 0 {T_0} T0表示基波周期, w 0 = 2 π / T 0 {w_0} = 2\pi /{T_0} w0=2π/T0为基波频率, c k {c_k} ck称为 x ( t ) x(t) x(t)的傅里叶级数,它可以用三角函数的线性组合来表示,即:
x ( t ) = a 0 + ∑ k = 1 + ∞ a k cos k w 0 t + ∑ k = 1 + ∞ b k sin k w 0 t 其中 a 0 = 1 T 0 ∫ T 0 x ( t ) d t , a k = 2 T 0 ∫ T 0 x ( t ) cos k w 0 t d t , b k = 2 T 0 ∫ T 0 x ( t ) sin k w 0 t d t x(t) = {a_0} + \sum\limits_{k = 1}^{ + \infty } {{a_k}\cos k{w_0}t} + \sum\limits_{k = 1}^{ + \infty } {{b_k}\sin k{w_0}t} 其中{a_0} = \frac{1}{{{T_0}}}\int_{{T_0}} {x(t)dt} ,{a_k} = \frac{2}{{{T_0}}}\int_{{T_0}} {x(t)\cos k{w_0}tdt} ,{b_k} = \frac{2}{{{T_0}}}\int_{{T_0}} {x(t)\sin k{w_0}tdt} x(t)=a0+k=1∑+∞akcoskw0t+k=1∑+∞bksinkw0t其中a0=T01∫T0x(t)dt,ak=T02∫T0x(t)coskw0tdt,bk=T02∫T0x(t)sinkw0tdt
因此该信号的傅里叶级数为 f ( t ) = 4 π ∑ k = 1 ∞ 1 2 k − 1 sin ( ( 2 k − 1 ) ω 0 t ) f(t)=\frac{4}{\pi}\sum\limits_{k=1}^{\infty}\frac{1}{2k-1}\sin((2k-1)\omega_0t) f(t)=π4k=1∑∞2k−11sin((2k−1)ω0t)其中, ω 0 = 2 π T 0 \omega_0=\frac{2\pi}{T_0} ω0=T02π为角频率, T 0 T_0 T0为信号的周期。
-
利用MATLAB绘出由前N次谐波合成的信号波形,观察随着N的变化合成信号波形的变化规律
绘制谐波合成信号代码如下:
clc; clear; close all t = -2 : 10^(-4) : 2; A = 1; tau = 1; % 脉冲宽度 T = 2; % 周期 Omega_0 = 2*pi/T; %基波频率 c0 = A*tau/T; rect_wave = mod(t, T) < tau; N = input('N='); f_N = c0 * ones(1,length(t)); %f_N(t) for k= 1 : 1 : N f_N = f_N + 2*A*tau/T *sinc(k*Omega_0*tau/ 2/pi) *cos(k*Omega_0*t); end % 绘图 subplot(2,1,1); plot(t, rect_wave, 'LineWidth', 2); xlabel('时间'); ylabel('幅度'); title('周期矩形脉冲信号'); subplot(2,1,2); plot(t, f_N, 'LineWidth', 2); xlabel('时间'); ylabel('幅度'); title(['前', num2str(N), '次谐波合成的周期矩形脉冲信号']);当N等于5时,N等于50时,N等于500时合成信号函数分别如下:

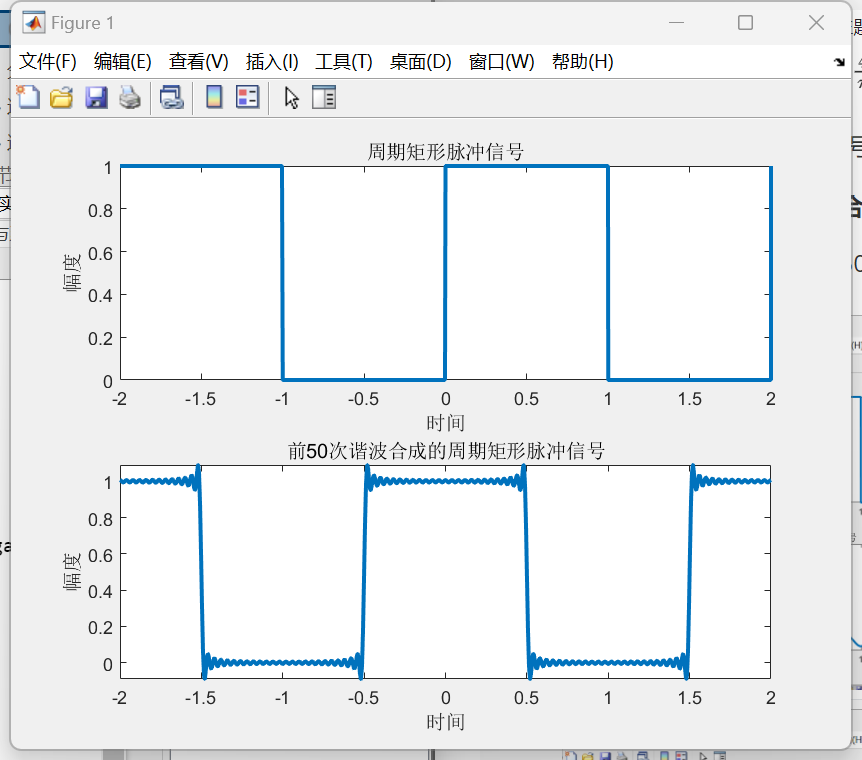

-
利用MATLAB绘出周期矩形脉冲信号的频谱,观察参数T和$\tau $变化时对频谱波形的影响
绘制周期矩形脉冲信号的频谱代码如下:
clc; clear; close all % 设置时间变量 t = -2:10^(-4):2; % 定义周期和占空比 T = 2; duty_cycle = 0.5; % 绘制周期矩形脉冲信号 rect_wave = mod(t, T) < duty_cycle*T; % 计算信号的傅里叶变换 fft_rect_wave = fftshift(fft(rect_wave)); % 计算频率轴坐标 fs = 1./(t(2)-t(1)); f = linspace(-fs/2, fs/2, length(t)); % 绘制频谱 figure(1) plot(f, abs(fft_rect_wave)./length(t), 'LineWidth', 2); xlabel('频率'); ylabel('幅度'); title(['周期为', num2str(T), '的矩形脉冲信号频谱']);绘制频谱图如下:

改变周期和占空比发现,频谱图像形状不变。
思考题
什么是吉伯斯现象?产生吉伯斯现象的原因是什么?
吉伯斯现象是指周期函数展开成傅里叶级数时,在级数和与原始函数之间可能出现的振荡现象。在周期性函数的跳跃处,傅里叶级数的部分和会以振荡的方式逐渐逼近跳跃值,直到最终趋于函数的跳跃值。
吉伯斯现象的出现是因为傅里叶级数在某些情况下不能完全收敛。
例如,对于一个具有跳跃的周期函数,它在跳跃点处的值不能通过傅里叶级数完全表示。因此,在跳跃点附近,傅里叶级数的部分和将以一种振荡的方式逼近跳跃值。这种振荡的幅度不会随着级数的增加而减小,而是会保持不变。
以周期矩形脉冲信号为例,说明周期信号的频谱有什么特点
- 频率分量为离散的正弦函数:周期矩形脉冲信号的频谱是由一系列正弦函数组成的。这些正弦函数对应了不同频率上的频率分量,在频域中呈现为离散的频率点。
- 频率分量间隔相等:在周期矩形脉冲信号的频谱中,每个频率分量之间的间隔相等,等于信号的基本频率,即原始信号的倒数。这是由于周期信号的频谱仅包含基波和谐波。
- 频率分量幅度逐渐下降:周期矩形脉冲信号的频谱中,随着频率的增大,各频率分量的幅度逐渐下降,而且下降得越来越快。这是由周期矩形脉冲信号的带宽限制所致,即信号带宽有限。
周期矩形脉冲信号的有效频带宽度与信号的时域宽度之间有什么关系?
周期矩形脉冲信号的有效频带宽度与信号的时域宽度存在正相关关系。对于周期矩形脉冲信号,其带限为 f max {f_{\max }} fmax和, f min {f_{\min }} fmin且它们的值可由脉冲的时域宽度 Δ t \Delta t Δt求得,即 f max = 1 / ( 2 Δ t ) {{f}_{\max }}={1}/{(2\Delta t)} fmax=1/(2Δt), f min = − 1 / ( 2 Δ t ) {{f}_{\min }}=-{1}/{(2\Delta t)}\; fmin=−1/(2Δt),因此,随着信号的时域宽度增加,其带宽也会相应地变宽,即有效频带宽度会增加;而如果信号的时域宽度减小,则其带宽也会变窄,即有效频带宽度会减小。
随着矩形脉冲信号参数 τ T \frac{\tau }{T} Tτ的变化,其频诺结构(如频谱包络形状、过零点、谱线间隔等)如何变化?
当 τ T \frac{\tau }{T} Tτ变大,也就是矩形脉冲信号的宽度变宽时,其频率响应的主瓣宽度(即频带宽度)变窄,主瓣峰值增加,同时高次谐波分量的幅值也会增强,频谱包络形状变尖锐,谱线间隔变宽。
而当变 τ T \frac{\tau }{T} Tτ小,矩形脉冲信号的宽度变窄时,其主瓣宽度变宽,主瓣峰值降低,高次谐波分量的幅值也会减小,这时频谱包络形状变得平缓,谱线间隔变窄。
(2)
已知x(t)是如下图所示的矩形脉冲信号

-
求该信号的傅里叶变换
利用MATLAB可快速求得该信号的傅里叶变换
syms t w >> y=int(2*exp(-j*w*t),t,-2,2); >> ezplot(y) (2sin(2w))/w因此求得其傅里叶变换为:(2sin(2w))/w
-
利用MATLAB绘出矩形脉冲信号的频谱,观察矩形脉冲宽度$\tau $变化时对频谱波形的影响
满足上述条件,实现代码如下:
% 设置采样步长 dt = 0.001; % 设置时间窗口大小 t = -1:dt:1; % 设置矩形脉冲宽度 tau = 0.2; % 构造矩形脉冲信号 x = rectpuls(t, tau); % 画出时域波形 subplot(2,1,1); plot(t, x); xlabel('时间 (s)'); ylabel('振幅'); title('时域信号波形'); % 进行傅里叶变换 y = fft(x) / length(x); % 计算频域采样间隔 df = 1 / (length(x) * dt); % 计算频率范围 f = (-length(x)/2:length(x)/2 - 1) * df; % 取实部并移动 y_shift = fftshift(y); y_abs = abs(real(y_shift)); % 画出频谱图 subplot(2,1,2); plot(f, y_abs); xlabel('频率 (Hz)'); ylabel('数量级'); title('矩形脉冲信号的频域');通过改变脉冲宽度
tau来观察矩形脉冲宽度的变化对频谱波形的影响,对比结果如下:

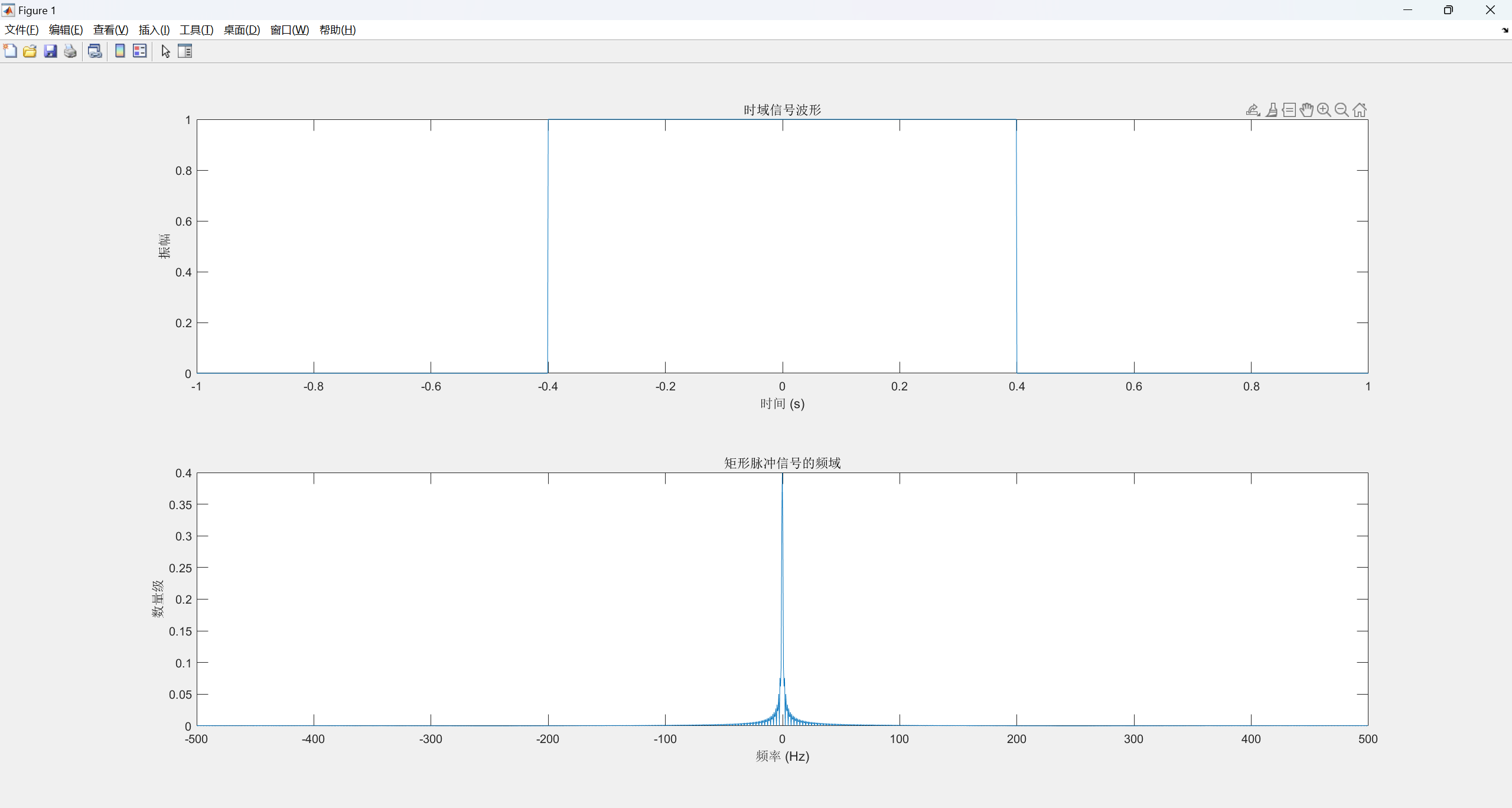

观察可知,当矩形脉冲宽度增大,振幅不变时,采样函数的主瓣宽度将缩窄,频域信号会变得更加集中,采样函数的峰值将减小,也就是说频域信号的幅度将变小;反之,当矩形脉冲宽度减小,振幅不变时,采样函数的主瓣宽度将变宽,频域信号会变得更加分散,采样函数的峰值将增大,也就是说频域信号的幅度将变大。
-
让矩形脉冲的面积始终等于1,改变矩形脉冲宽度,观察矩形买成信号时域波形和频谱随矩形脉冲宽度的变化趋势
满足上述条件,实现代码如下:
% 设置采样步长 dt = 0.001; % 设置时间窗口大小 t = -1:dt:1; % 设置矩形脉冲宽度 tau = 0.6; % 构造矩形脉冲信号 x = (1/tau).*rectpuls(t, tau); % 画出时域波形 subplot(2,1,1); plot(t, x); xlabel('时间 (s)'); ylabel('振幅'); title('时域信号波形'); % 进行傅里叶变换 y = fft(x) / length(x); % 计算频域采样间隔 df = 1 / (length(x) * dt); % 计算频率范围 f = (-length(x)/2:length(x)/2 - 1) * df; % 取实部并移动 y_shift = fftshift(y); y_abs = abs(real(y_shift)); % 画出频谱图 subplot(2,1,2); plot(f, y_abs); xlabel('频率 (Hz)'); ylabel('数量级'); title('矩形脉冲信号的频域');通过改变脉冲宽度
tau来观察矩形脉冲宽度的变化对频谱波形的影响,对比结果如下:



观察可知,当矩形脉冲宽度增大,面积不变时,采样函数的主瓣宽度将缩窄,频域信号会变得更加集中,采样函数的峰值不变;反之,当矩形脉冲宽度减小,振幅不变时,采样函数的主瓣宽度将变宽,频域信号会变得更加分散,采样函数的峰值不变。
思考题
比较矩形脉冲信号和周期矩形脉冲信号的频谱,两者之间有何异同?
相同点:两者的频谱图外观相似。
不同点:前者是由无限个不同频率的正弦波叠加而成的连续谱线,后者则是由一组离散谐波分量组成的预定频率分布。
根据矩形脉冲宽度 τ \tau τ变化时频谱的变化律,说明信号的有效频带宽度与其时域宽度之间有什么关系。当脉冲宽度 τ → 0 \tau \to 0 τ→0,脉冲的面积始终等于1,其频谱有何特点?
矩形脉冲信号的频谱谱线随着矩形脉冲宽度的增加会逐渐集中,但幅度却会逐渐减小。因此,当矩形脉冲宽度 τ \tau τ变小时,其频带宽度应该会变窄,而且能量集中在频谱的高频处。此外,当脉冲宽度 τ → 0 \tau \to 0 τ→0时,脉冲的面积始终等于1,其频域特点即为全频带连续光谱,其频谱密度为常数,不随频率变化而发生改变。
(3)
已知x(n)是如下图所示的周期方波序列

利用MATLAB绘制周期方波序列的频谱波形,改变参数N和N1的大小,观察频谱波形的变化趋势。
实现代码如下,通过改变周期T和占空比可以改变参数N和N1的大小
clc
clear;
close all;
% 生成方波序列
k = 0:99;
N = 100;
T = 20;
x = square(2*pi*k/T,80)/2+0.5;
% 时域图像
subplot(4,1,1);
stem(k,x,"filled");
xlabel('n');
ylabel('x(n)');
title('时域图像');
X = fft(x);
%频谱图
subplot(4,1,2)
stem(k,X,"filled")
xlabel('f');
ylabel('X(f)');
title('频谱图');
% 频谱的幅谱图
mag_X = abs(X);
f = (0:N-1)/N;
subplot(4,1,3);
stem(f,mag_X,'filled');
xlabel('f');
ylabel('|X(f)|');
title('频谱的幅谱图');
% 频谱的相谱图
phase_X = angle(X);
subplot(4,1,4);
stem(f,phase_X,"filled");
xlabel('f');
ylabel('∠X(f)');
title('频谱的相谱图');
当N=10,N1=5时,频谱如下:
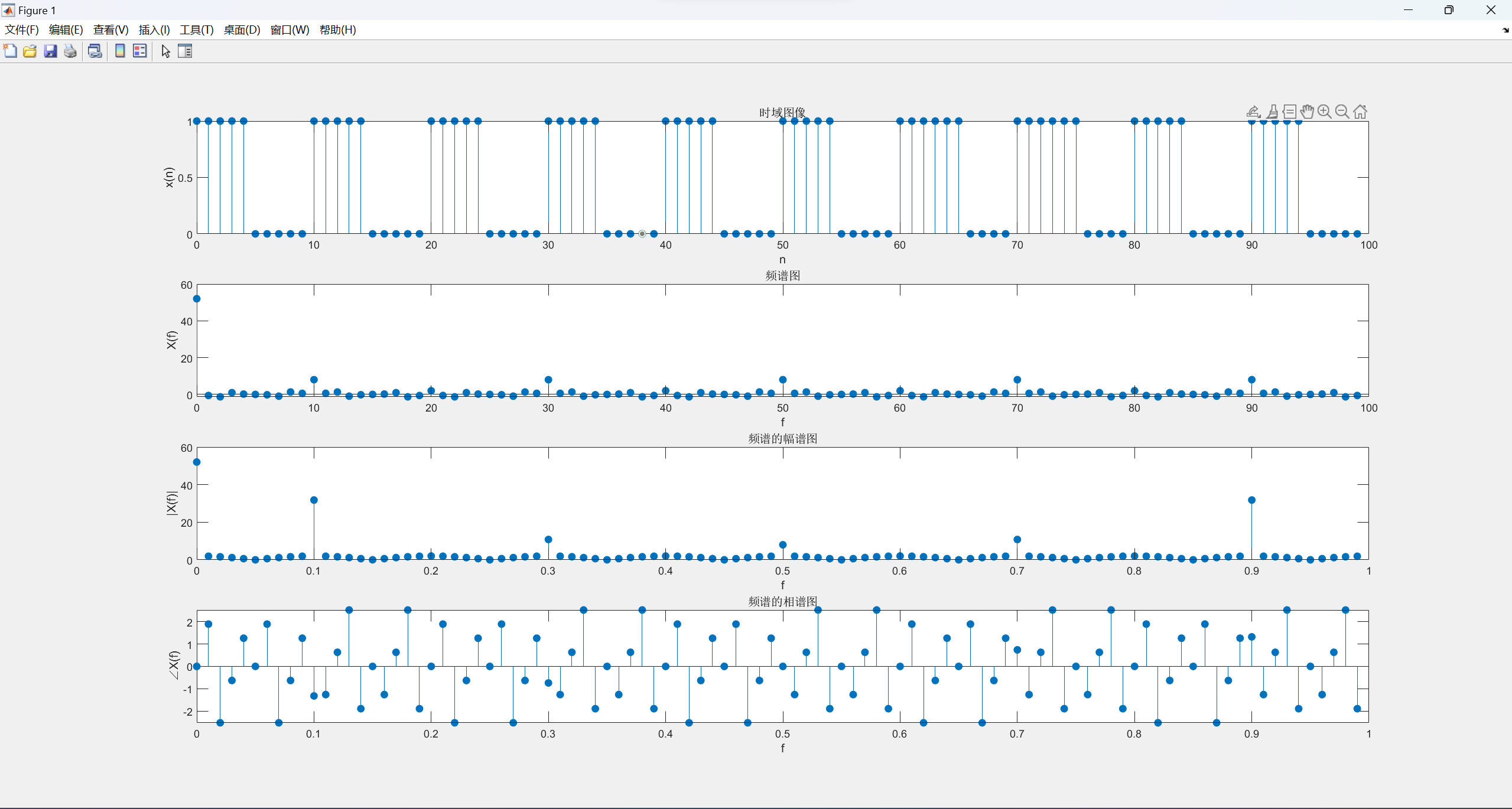
当N=20,N1=10时,频谱如下:

当N=10,N1=2时,频谱如下:

当N=10,N1=8时,频谱如下:
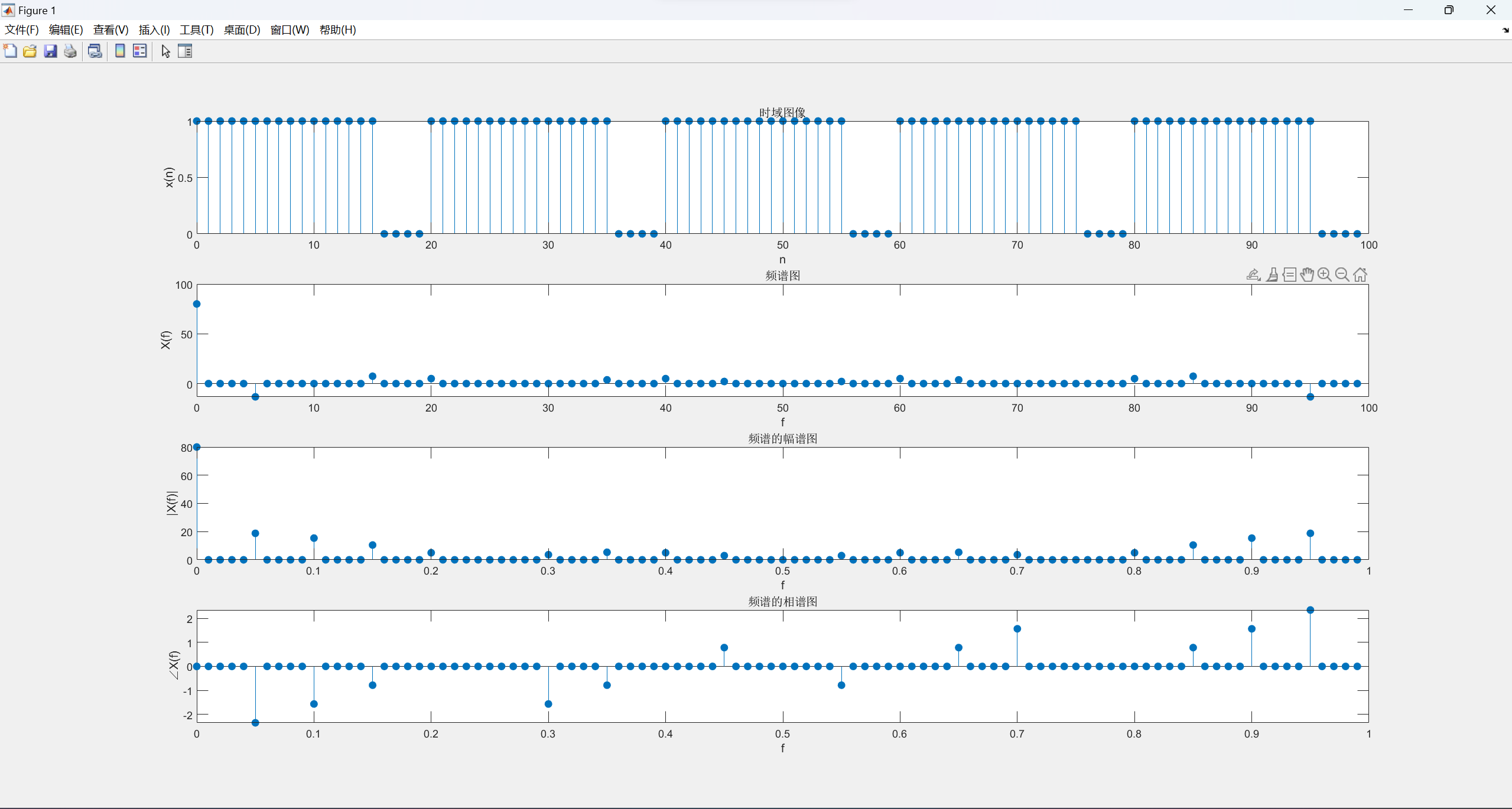
思考题
以周期方波序列为例,说明周期序列与连续周期信号的频谱有何异同
相同点:
都是周期信号,在频域中都只有离散的频率分量;
都可以通过傅里叶变换计算得到频谱。
不同点:
周期序列的频率分量是离散的,且存在一个最高频率,超过这个频率将会出现混叠效应;
连续周期信号的频率分量是连续的,没有采样频率的限制,因此通常比周期序列的频谱更加精确;
对于周期方波序列而言,其频谱幅值仅包含基频和其奇次谐波分量,而相位差为$\pm \pi $。而对于一般的连续周期信号而言,其频谱幅值和相位会更加复杂,存在无数种不同的变化规律。
随着周期方波序列占空比的变化,其频谱如何随之变化?
当占空比大于 50%时,频谱中的偶次谐波分量幅度逐渐减小,奇次谐波分量的幅度逐渐增大;
当占空比为50%时,离散周期方波序列的频谱中只有基频分量存在,并且其幅值最大;
当占空比小于50%时,离散周期方波序列的基频分量幅值开始递减,而奇次谐波分量的幅值则开始递增;
当占空比接近0%时,离散周期方波序列的基频分量幅值几乎为0,而奇次谐波分量的幅值则变得越来越大。
(4)
已知一脉冲序列
x
(
n
)
=
{
1
,
∣
n
∣
⩽
N
1
;
0
,
∣
n
∣
>
N
1
}
x(n) = \left\{ 1,\left| n \right| \leqslant {N_1} ; 0,\left| n \right| > {N_1} \ \right\}
x(n)={1,∣n∣⩽N1;0,∣n∣>N1 }
利用MATLAB绘制周期方波序列的频谱波形,改变矩形脉冲序列的宽度,观察频谱波形的变化趋势。
实现代码如下:
clc;
clear;
close all
w = -pi:0.01*pi:pi;%对频率轴采样
n = 5;%通过改变n的值来改变N1
k = -n:n;
x = ones(size(k));
subplot(4,1,1)
stem(k,x,"filled");
xlabel('n')
title('x(n)')
X = x*exp(-1i*k'*w);
subplot(4,1,2)
plot(w/pi,abs(X))
xlabel('\Omega/\pi')
title('|X(e^j^\Omega)|')
% 频谱的幅谱图
mag_X = abs(X);
subplot(4,1,3);
stem(w/pi,mag_X,'filled');
xlabel('f');
ylabel('|X(f)|');
title('频谱的幅谱图');
% 频谱的相谱图
phase_X = angle(X);
subplot(4,1,4);
stem(w/pi,phase_X,"filled");
xlabel('f');
ylabel('∠X(f)');
title('频谱的相谱图');
当N1=5时,图像如下:

当N1=7时,图像如下:

当N1=9时,图像如下:

当N1=3时,图像如下:

当N1=1时,图像如下:

观察上述图像,对比可以发现,当矩形脉冲序列宽度较小时,其频谱谱形比较平缓,没有明显的峰值,且频谱图像的峰值较小;当矩形脉冲序列宽度增加时,其频谱图像开始出现明显的峰值,且频谱图像的峰值变大,图像变窄,说明矩形脉冲序列宽度与其频谱的有效频带宽度成反比。
四、心得体会
通过本次实验,我系统且具体地了解了LTI系统的时域分析,这对我对这方面的学习有很大帮助。
实验四 LTI系统的频域分析
一、实验目的
- 加深LTI系统频率响应基本概念的掌握和理解。
- 学习和掌握LTI系统频率特性的分析方法。
二、实验原理
- 连续时间系统的频率响应
- 离散时间系统的频率响应
三、实验内容
(1)
已知一个RLC电路构造的二阶高通滤波器如下图所示,其中 R = L 2 C , L = 0.4 H , C = 0.05 F R = \sqrt {\frac{L}{{2C}}} ,L = 0.4H,C = 0.05F R=2CL,L=0.4H,C=0.05F

-
计算该电路系统的频率响应及高通截至频率;
根据电路可以计算出:
y ′ ′ ( t ) + 10 y ′ ( t ) + 50 y ( t ) = x ′ ′ ( t ) y''(t) + 10y'(t) + 50y(t) = x''(t) y′′(t)+10y′(t)+50y(t)=x′′(t)
所以其频率响应为:
H ( w ) = ( j w ) 2 ( j w ) 2 + 10 j w + 50 H(w) = \frac{{{{(jw)}^2}}}{{{{(jw)}^2} + 10jw + 50}} H(w)=(jw)2+10jw+50(jw)2
令 H ( w ) = 2 2 H(w) = \frac{{\sqrt 2 }}{2} H(w)=22,则高通截至频率为w=7.0711 Hz -
利用MATLAB绘制幅度响应和相位响应曲线,比较系统的频率特性与理论计算的结果是否一致。
实现代码如下:
clc; clear; close all b = [0.04 0 0]; a = [0.04 0.4 2]; [H, w]=freqs(b,a,2000); subplot(2,1,1); plot(w,abs(H)); yticks([0 0.4 0.707]) set(gca,'xtick',[0:10:100]); xlabel('\omega(rad/s)'); ylabel('Magnitude'); title('|H(j\omega)|'); grid on; subplot(2,1,2); plot(w,angle(H)); set(gca,'xtick',[0:10:1000]); xlabel('\omega(rad/s)'); ylabel('Phase'); title('\phi(\omega)')运行结果如下:

比较结果可知,幅度为0.707,时域频率为7.07rad/s,系统的频率特性与理论计算结果一致。
(2)
已知一个RC电路如下图所示

-
对不同的RC值,用MATLAB画出系统的幅度响应曲线 ∣ H ( w ) ∣ \left| {H(w)} \right| ∣H(w)∣,观察实验结果分析图示RC电路具有什么样的频率特性(高通、低通、带通或带阻)?系统的频率特性随着RC值的改变,有何变化规律?
由题可知,系统的微分方程为:
R C y ′ ( t ) + y ( t ) = x ( t ) RCy'(t) + y(t) = x(t) RCy′(t)+y(t)=x(t)
编写代码如下:clc; clear; close all % 定义RC电路的电阻R和电容C R = 1e3; C_values = [1e-9, 10e-9, 100e-9]; % 定义频率范围和步长 f = logspace(0, 7, 10000); figure; hold on; for i = 1:length(C_values) C = C_values(i); w_c = 1 / (R * C); % 计算截止角频率 % 计算幅度响应 H = 1 ./ (1 + 1j * f / w_c); mag = abs(H); % 绘制幅度响应曲线 semilogx(f, 20*log10(mag), 'DisplayName', ['RC=' num2str(R) 'Ω, C=' num2str(C*1e9) 'nF']) end % 设置图表属性 grid on; xlabel('频率 (Hz)'); ylabel('幅度响应 (dB)'); title('RC电路的幅度响应'); legend('Location', 'SouthWest');运行结果如下:

从图中可以看出,当 ω \omega ω时,幅度响应逼近于 1;
当 $\omega \to \infty $时,幅度响应逼近于 0,这意味着该电路是一个低通滤波器。
随着RC值的增加(或C值的减小),截止角频率 ω \omega ω将增加,低通滤波器的截止频率也越来越高。
因此可以得出结论:该RC电路是一个低通滤波器,其频率特性随着RC值的改变而改变,具有如下规律:
- 当RC减小时,截止频率 ω c \omega_c ωc也会减小,电路可以通过更高的频率信号,因此具有更高通的特性。
- 当RC增大时,截止频率 ω c \omega_c ωc也会增大,电路不能通过更高的频率信号,从而具有更低通的特性。
- 当RC接近某个临界值时,电路具有最接近理论高通特性和低通特性的带通特性。
-
系统输人信号 x ( t ) = c o s ( 100 t ) 十 c o s ( 3000 t ) , t = 0 0.2 s x(t)=cos(100t)十cos(3000t),t=0~0.2s x(t)=cos(100t)十cos(3000t),t=0 0.2s,该信号包含了一个低频分量和一个高频分量。试确定适当的RC值,滤除信号中的高频分量。并绘出滤波前后的时域信号波形及系统的频率响应曲线。
编写代码如下:
clc; clear; close all t=0:0.0001:0.2; x=cos(100*t)+cos(3000*t); subplot(4,1,1); plot(t,x);%滤波前 xlabel('t/s'); ylabel('x(t)'); title('时域波形(滤波前)'); %设置RC C=1e-4; R=100; b=[1]; a=[C*R 1]; [H,w]=freqs(b,a,3000); y=abs (H(100)).*cos(100*t+angle(H(100)))+abs (H(3000)).*cos(3000*t+angle(H(3000))); subplot(4,1,2); plot(t,y);%滤波后 xlabel('t/s'); ylabel('x(t)') ; title('时域波形(滤波后)'); subplot(4,1,3); plot(w,abs (H)); set(gca,'ytick',[0 0.4 0.707]);xlabel(' omega(rad/s');ylabel('Magnitude'); title('|H(j\omega)|'); grid on; subplot(4,1,4); plot(w,angle(H)); xlabel('\omega(rad/s'); ylabel('Phase'); title( 'phi(\omega)'); grid on;实验结果如下:

多次调整可知,当设置C=10-4F,R=100Ω左右,滤波效果最好。
(3)
已知离散系统的系统框图如下图所示

-
写出M=8时系统的差分方程和系统函数;
由题可知,M=8的系统差分方程为:
y ( n ) = x ( n ) + x ( n − 1 ) + ⋯ + x ( n − 8 ) y(n) = x(n) + x(n - 1) + \cdots + x(n - 8) y(n)=x(n)+x(n−1)+⋯+x(n−8)
系统函数为:
H ( z ) = 1 + z − 1 + z − 2 + ⋯ + z − 8 H(z) = 1 + {z^{ - 1}} + {z^{ - 2}} + \cdots + {z^{ - 8}} H(z)=1+z−1+z−2+⋯+z−8 -
利用MATLAB计算系统的单位抽样响应;
编写代码如下:
clc; clear; close all b = [1 1 1 1 1 1 1 1 1]; a = [1]; subplot(3,1,1); impz(b,a,0:19);计算得系统的单位抽样响应:

-
试利用MATLAB绘出其系统零极点分布图、幅频和相频特性曲线,并分析该系统具有怎样的频率特性。
编写程序如下:
clc; clear; close all b = [1 1 1 1 1 1 1 1 1]; a = [1]; subplot(3,1,1); zplane(b,a); [H,w]=freqz(b,a); subplot(3,1,2); plot(w/pi,abs(H)); xlabel('\omega(\pi)') ; ylabel('Magnitude'); title('|H(e^j^\omega)'); grid on; subplot(3,1,3); plot(w/pi,angle(H)/pi); xlabel('\omega(\pi)'); ylabel('Phase(\pi)') ; title('\theta(\omega)') ; grid on;画出系统零极点分布图,幅频和相频特性曲线,如下:
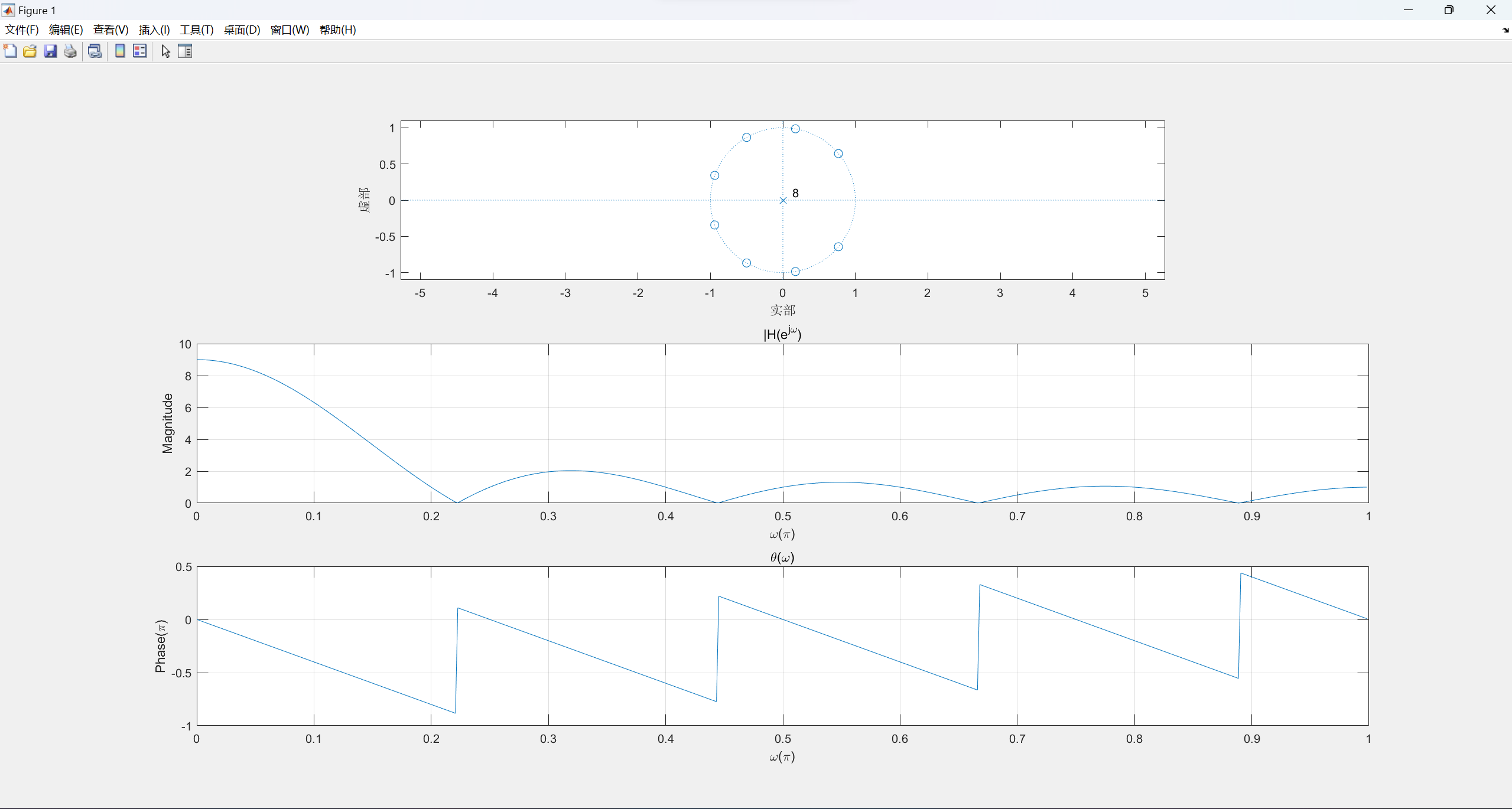
从幅频图可以看出该系统具有低通的频率特性。
b = [1 0 0 0 0 0 0 0 -1];
a = [1 -1 0 0 0 0 0 0 0]。
(4)
已知一离散时间LTI系统的频率响应 H ( e j Ω ) H({e^{j\Omega }}) H(ejΩ)如下图所示,输人信号为 x ( n ) = cos ( 0.3 π n ) + 0.5 cos ( 0.8 π n ) x(n) = \cos (0.3\pi n) + 0.5\cos (0.8\pi n) x(n)=cos(0.3πn)+0.5cos(0.8πn)。试根据式(8-38)分析正弦信号 sin ( Ω ) \sin (\Omega ) sin(Ω)通过频率响应为 H ( e j Ω ) H({e^{j\Omega }}) H(ejΩ)的离散时间系统的响应,并根据分析结果计算系统对于 x ( n ) x(n) x(n)的响应 y ( n ) y(n) y(n),用MATLAB绘出系统输人与输出波形。
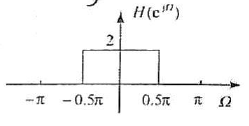
观察实验结果,分析图示系统具有什么样的频率特性(高通、低通、带通或带阻)?从输入输出信号上反映出系统的频率特性?
编写代码如下:
clc;
clear;
close all
n=0:19;
x=cos(0.3*pi*n)+0.5*cos(0.8*pi*n);
subplot(2,1,1);
stem(n,x,'filled')
xlabel('n');
title('x(n)');
subplot(2,1,2);
y=cos(0.3*pi*n);
stem(n,y,'filled')
xlabel('n');
title('y(n)');
得到结果如下:

分析可知,系统具有低通特性,由输入信号变化的快慢可以得知。
四、心得体会
通过本次实验,我系统且具体地了解了LTI系统的频域分析,这对我对这方面的学习有很大帮助。
实验五 连续时间系统的复频域分析
一、实验目的
- 掌握拉普拉斯变换及其反变换的定义,并掌握 MATLAB实现方法。
- 学习和掌握连续时间系统系统函数的定义及复频域分析方法。
- 掌握系统零极点的定义,加深理解系统零极点分布与系统特性的关系。
二、实验原理
- 拉普拉斯变换
- 连续时间系统的系统函数
- 连续时间系统的零极点分析
三、实验内容
(1)
已知系统的冲激响应 h ( t ) = u ( t ) − u ( t − 2 ) h(t)=u(t)-u(t-2) h(t)=u(t)−u(t−2),输信号 x ( t ) = u ( t ) x(t)=u(t) x(t)=u(t)试采用复频域的方法求解系统的响应,编写MATLAB程序实现。
编写程序如下:
clc
clear;
close all;
syms t
x = heaviside(t);
X = laplace(x);
h = heaviside(t)-heaviside(t-2);
H = laplace(h);
Y = H*X;
y = ilaplace(Y);
%输出y的表达式
y
编写代码运行得到结果如下:
y =
t - heaviside(t - 2)*(t - 2)
(2)
已知因果连续时间系统的系统函数分别如下:
- H ( s ) = 1 s 3 + 2 s 2 + 2 s + 1 H(s) = \frac{1}{{{s^3} + 2{s^2} + 2s + 1}} H(s)=s3+2s2+2s+11
- H ( s ) = s 2 + 1 s 5 + 2 s 4 − 3 s 3 + 3 s 2 + 2 H(s) = \frac{{{s^2} + 1}}{{{s^5} + 2{s^4} - 3{s^3} + 3{s^2} + 2}} H(s)=s5+2s4−3s3+3s2+2s2+1
试采用MATLAB画出其零极点分布图,求解系统的冲激响应 h ( t ) h(t) h(t)和频率响应 H ( w ) H(w) H(w)并判断系统是否稳定。
编写代码如下:
对 H ( s ) = 1 s 3 + 2 s 2 + 2 s + 1 H(s) = \frac{1}{{{s^3} + 2{s^2} + 2s + 1}} H(s)=s3+2s2+2s+11:
clc
clear;
close all;
a = [1 2 2 1];
b = [1];
sys = tf(b,a);
subplot(2,2,1)
pzmap(sys);
[r,p,k] = residue(b,a);
syms s
H = 1/(s^3+2*s^2+2*s+1);
h = ilaplace(H);
subplot(2,2,2)
impulse(sys);
[H,w]=freqs(b,a);
subplot(2,2,3)
plot(w,abs(H));
xlabel('\omega(rad/s)');
ylabel('Magnitude');
title('|H(j\omega)|');
grid on;
subplot(2,2,4)
plot(w,angle(H));
xlabel('\omega(rad/s)');
ylabel('\phi(\omega)');
ylabel('Phase');
title('\phi(\omega)');
grid on;
对 H ( s ) = s 2 + 1 s 5 + 2 s 4 − 3 s 3 + 3 s 2 + 2 H(s) = \frac{{{s^2} + 1}}{{{s^5} + 2{s^4} - 3{s^3} + 3{s^2} + 2}} H(s)=s5+2s4−3s3+3s2+2s2+1:
clc
clear;
close all;
a = [5 2 -3 3 3 2];
b = [1 0 1];
sys = tf(b,a);
subplot(2,2,1)
pzmap(sys);
[r,p,k] = residue(b,a);
syms s
H = (s^2+1)/(s^5+2*s^4-3*s^3+3*s^2+3*s+2);
h = ilaplace(H);
subplot(2,2,2)
impulse(sys);
[H,w]=freqs(b,a);
subplot(2,2,3)
plot(w,abs(H));
xlabel('\omega(rad/s)');
ylabel('Magnitude');
title('|H(j\omega)|');
grid on;
subplot(2,2,4)
plot(w,angle(H));
xlabel('\omega(rad/s)');
ylabel('\phi(\omega)');
ylabel('Phase');
title('\phi(\omega)');
grid on;
对 H ( s ) = 1 s 3 + 2 s 2 + 2 s + 1 H(s) = \frac{1}{{{s^3} + 2{s^2} + 2s + 1}} H(s)=s3+2s2+2s+11运行结果如下:
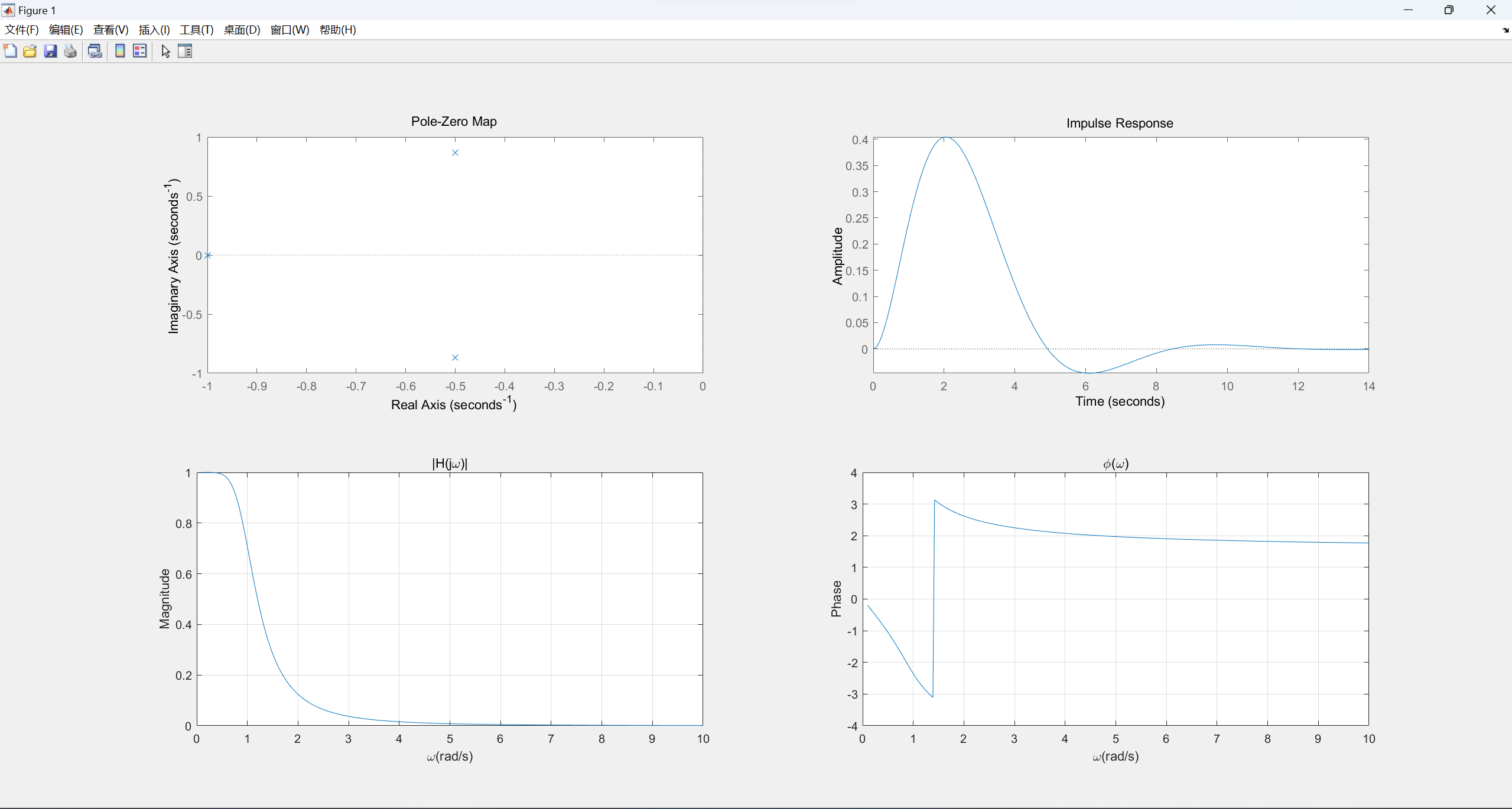
观察零极图可以看出,H(s)的所有几点均位于s左半平面,故系统稳定。
输出r和p的值如下:
>> r
r =
1.0000 + 0.0000i
-0.5000 - 0.2887i
-0.5000 + 0.2887i
>> p
p =
-1.0000 + 0.0000i
-0.5000 + 0.8660i
-0.5000 - 0.8660i
因此可以得到:
H
(
s
)
=
1
s
+
1
+
−
0.5
−
0.2887
j
s
+
0.5
−
0.866
j
+
−
0.5
+
0.2887
j
s
+
0.5
+
0.866
j
H(s) = \frac{1}{{s + 1}} + \frac{{ - 0.5 - 0.2887j}}{{s + 0.5 - 0.866j}} + \frac{{ - 0.5 + 0.2887j}}{{s + 0.5 + 0.866j}}
H(s)=s+11+s+0.5−0.866j−0.5−0.2887j+s+0.5+0.866j−0.5+0.2887j
根据拉氏变换得到:
h
(
t
)
=
e
−
t
+
(
−
0.5
−
0.2887
j
)
e
−
0.5
+
0.866
j
+
(
−
0.5
+
0.2887
j
)
e
−
0.5
−
0.866
j
h(t) = {e^{ - t}} + ( - 0.5 - 0.2887j){e^{ - 0.5 + 0.866j}} + ( - 0.5 + 0.2887j){e^{ - 0.5 - 0.866j}}
h(t)=e−t+(−0.5−0.2887j)e−0.5+0.866j+(−0.5+0.2887j)e−0.5−0.866j
对
H
(
s
)
=
s
2
+
1
s
5
+
2
s
4
−
3
s
3
+
3
s
2
+
2
H(s) = \frac{{{s^2} + 1}}{{{s^5} + 2{s^4} - 3{s^3} + 3{s^2} + 2}}
H(s)=s5+2s4−3s3+3s2+2s2+1运行结果如下:

从零极图可以看出,H(s)有两个极点位于s右半平面,故系统是不稳定的。
输出r和p的值如下:
>> r
r =
0.1277 + 0.0000i
-0.0341 - 0.0492i
-0.0341 + 0.0492i
-0.0298 - 0.1226i
-0.0298 + 0.1226i
>> p
p =
-1.1803 + 0.0000i
0.7391 + 0.6886i
0.7391 - 0.6886i
-0.3489 + 0.4586i
-0.3489 - 0.4586i
因此可以得到:
H
(
s
)
=
0.0769
s
+
3.1704
+
−
0.03
−
0.0881
j
s
−
(
0.9669
+
0.9540
j
)
+
−
0.03
+
0.0881
j
s
−
(
0.9669
−
0.9540
j
)
+
−
0.0085
−
0.1436
j
s
−
(
−
0.3817
+
0.4430
j
)
+
−
0.0085
+
0.1436
j
s
−
(
−
0.3817
−
0.4430
j
)
H(s) = \frac{{0.0769}}{{s + 3.1704}} + \frac{{ - 0.03 - 0.0881j}}{{s - (0.9669 + 0.9540j)}} + \frac{{ - 0.03 + 0.0881j}}{{s - (0.9669 - 0.9540j)}} + \frac{{ - 0.0085 - 0.1436j}}{{s - ( - 0.3817 + 0.4430j)}} + \frac{{ - 0.0085 + 0.1436j}}{{s - ( - 0.3817 - 0.4430j)}}
H(s)=s+3.17040.0769+s−(0.9669+0.9540j)−0.03−0.0881j+s−(0.9669−0.9540j)−0.03+0.0881j+s−(−0.3817+0.4430j)−0.0085−0.1436j+s−(−0.3817−0.4430j)−0.0085+0.1436j
根据拉氏变换得到:
h
(
t
)
=
0.0769
e
−
3.1704
t
−
0.12
e
0.9669
t
cos
(
0.0881
t
)
−
0.3524
e
0.9669
t
sin
(
0.0881
t
)
+
0.017
e
0.3817
t
cos
(
0.1436
t
)
−
0.2872
e
0.3817
t
sin
(
0.1436
t
)
h(t) = 0.0769{e^{ - 3.1704t}} - 0.12{e^{0.9669t}}\cos (0.0881t) - 0.3524{e^{0.9669t}}\sin (0.0881t) + 0.017{e^{0.3817t}}\cos (0.1436t) - 0.2872{e^{0.3817t}}\sin (0.1436t)
h(t)=0.0769e−3.1704t−0.12e0.9669tcos(0.0881t)−0.3524e0.9669tsin(0.0881t)+0.017e0.3817tcos(0.1436t)−0.2872e0.3817tsin(0.1436t)
(3)
已知连续时间系统函数的极点位置分别如下所示(设系统无零点):
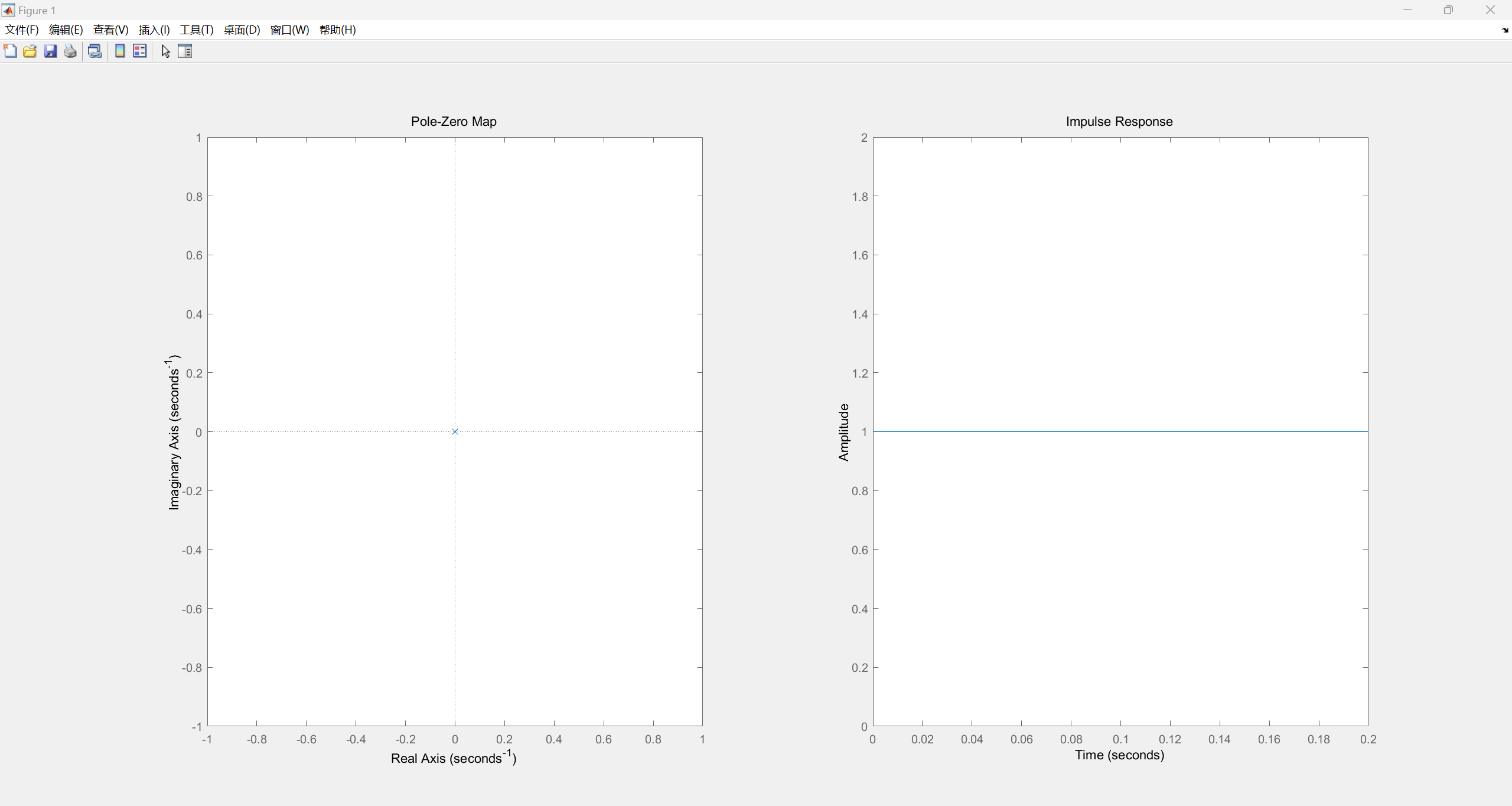
- p=0
- p=-2
- p=2
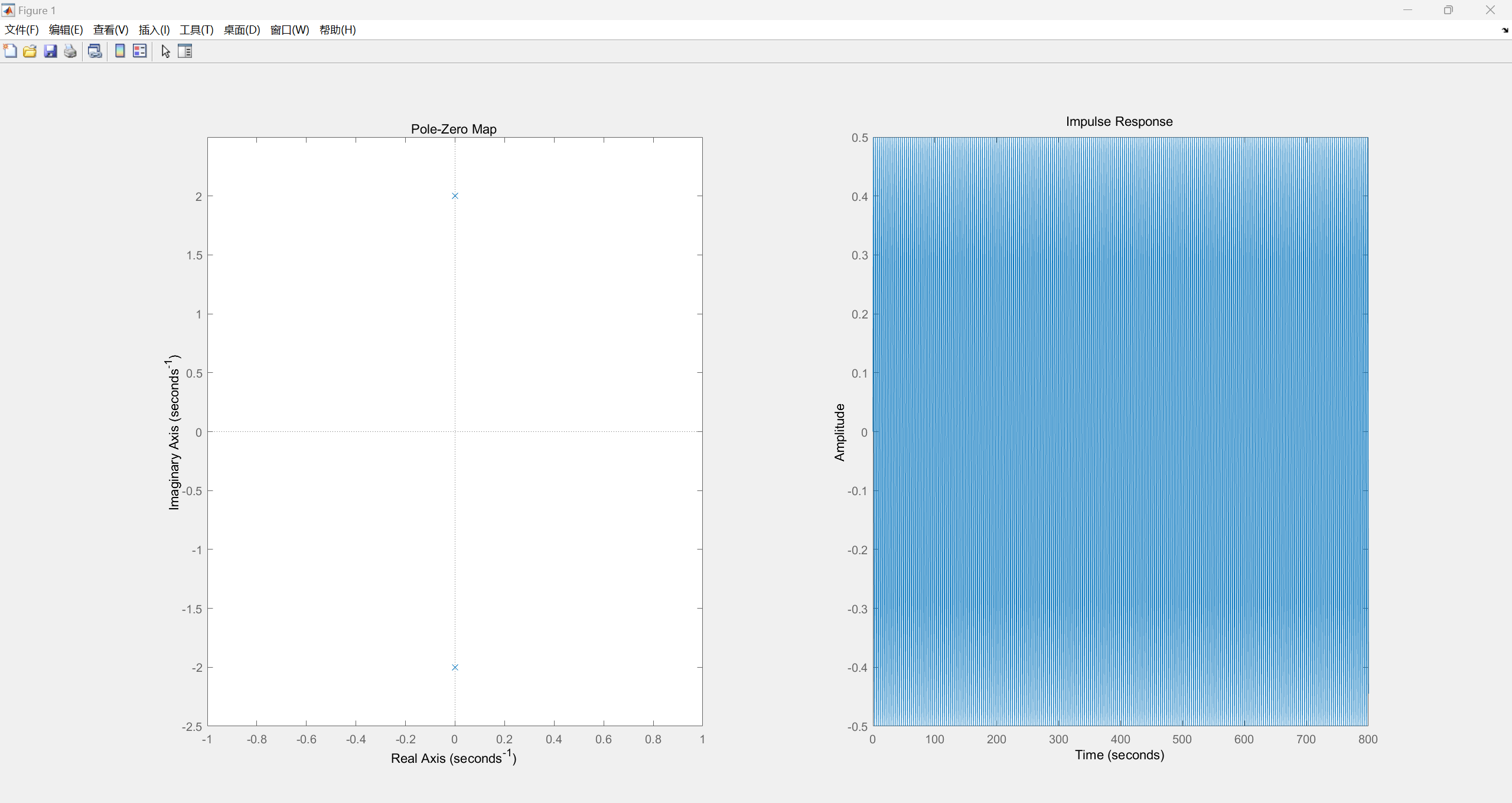
- p1=2j,p2=-2j
- p1=-1+4j,p2=-1-4j
- p1=1+4j,p2=1-4j
试用MATLAB绘制上述6种不同情况下,系统函数的零极点分布图并绘制相应冲激响应的时域波形,观察并分析系统函数极点位置对冲激响应时域特性的影响。
编写程序如下:
clc
clear;
close all;
z = [];
p = [2j, -2j];
k = 1;
[b,a] = zp2tf(z,p,k);
sys = tf(b,a);
subplot(1,2,1);
pzmap(sys);
subplot(1,2,2)
impulse(sys)
只需改变p的值即可.
运行结果如下:
p=0
p=-2

p=2

p1=2j,p2=-2j
p1=-1+4j,p2=-1-4j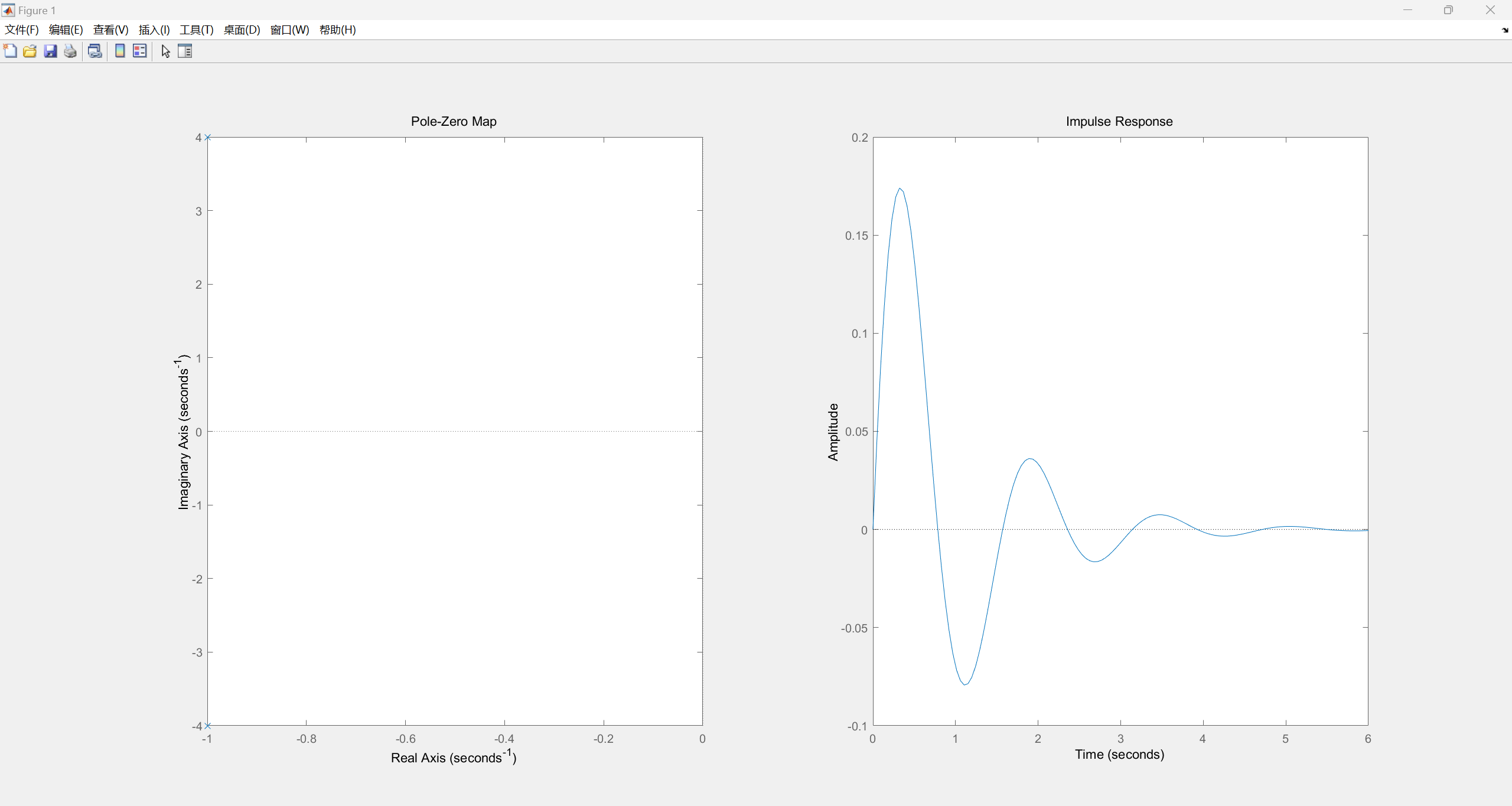
p1=1+4j,p2=1-4j

观察上述零极点分布以及相应冲激响应波形可以看出,当极点位于坐标轴左半平面时,冲激响应绝对可积,系统稳定;反之则冲激响应发散,系统不稳定。
(4)
已知连续时间系统的系统函数分别如下:
- H ( s ) = 1 s 2 + 2 s + 17 H(s) = \frac{1}{{{s^2} + 2s + 17}} H(s)=s2+2s+171
- H ( s ) = s + 8 s 2 + 2 s + 17 H(s) = \frac{{s + 8}}{{{s^2} + 2s + 17}} H(s)=s2+2s+17s+8
- H ( s ) = s − 8 s 2 + 2 s + 17 H(s) = \frac{{s - 8}}{{{s^2} + 2s + 17}} H(s)=s2+2s+17s−8
上述3个系统具有相同的极点,只是零点不同,试用MATLAB分别绘制系统的零极点分布图及相应冲激响应的时域波形,观察并分析系统函数零点位置对冲激响应时域特性的影响。
编写代码如下:
clc
clear;
close all;
a = [1 2 17];
b = [1];
sys = tf(b,a);
subplot(1,2,1)
pzmap(sys);
subplot(1,2,2)
impulse(sys);
改变b的值得到其它数据。
得到的结果如下:
对于 H ( s ) = 1 s 2 + 2 s + 17 H(s) = \frac{1}{{{s^2} + 2s + 17}} H(s)=s2+2s+171:
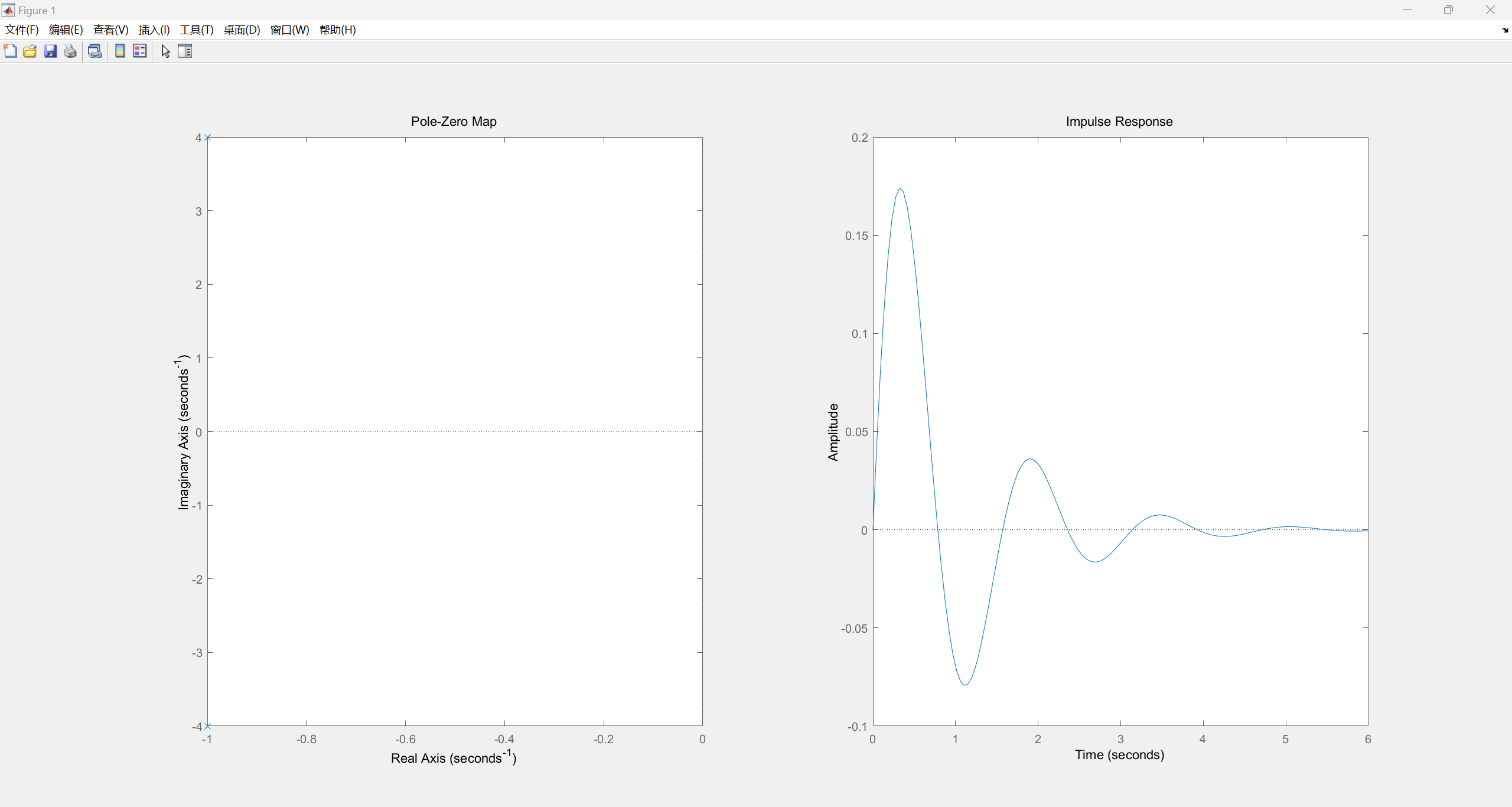
对于 H ( s ) = s + 8 s 2 + 2 s + 17 H(s) = \frac{{s + 8}}{{{s^2} + 2s + 17}} H(s)=s2+2s+17s+8:

对于 H ( s ) = s − 8 s 2 + 2 s + 17 H(s) = \frac{{s - 8}}{{{s^2} + 2s + 17}} H(s)=s2+2s+17s−8:

观察上述图像可以发现,三个图像的波形基本相同,但是幅度和相位不同,这就是零点分布不同导致的。
四、心得体会
通过本次实验,我系统且具体地了解了连续时间系统的复频域分析,这对我对这方面的学习有很大帮助。
实验六 离散时间系统的z域分析
一、实验目的
- 掌握之变换及其反变换的定义,并掌握MATLAB实现方法;
- 学习和掌握离散时间系统系统函数的定义及z域分析方法;
- 掌握系统零极点的定义,深理解系统零极点分布与系统特性的关系
二、实验原理
- z变换
- 离散时间系统的系统函数
- 离散时间系统的零极点分析
三、实验内容
(1)
已知因果离散时间系统的系统函数分别为:
- H ( z ) = z 2 + 2 z + 1 z 3 − 0.5 z 2 − 0.005 z + 0.3 H(z) = \frac{{{z^2} + 2z + 1}}{{{z^3} - 0.5{z^2} - 0.005z + 0.3}} H(z)=z3−0.5z2−0.005z+0.3z2+2z+1
- H ( z ) = z 3 − z 2 + 2 3 z 4 + 3 z 3 − z 2 + 3 z − 1 H(z) = \frac{{{z^3} - {z^2} + 2}}{{3{z^4} + 3{z^3} - {z^2} + 3z - 1}} H(z)=3z4+3z3−z2+3z−1z3−z2+2
试采用MATLAB画出其零极点分布图,求解系统的冲激响应 h ( n ) h(n) h(n)和频率响应 H ( e j Ω ) H({e^{j\Omega }}) H(ejΩ)并判断系统是否稳定。
编写代码如下:
clc
clear;
close all;
a = [1 -0.5 -0.005 0.3];
b = [1 2 1];
subplot(2,2,1)
zplane(b,a);
[r,p,k]=residue(b,a);
subplot(2,2,2)
impz(b,a);
[H,w]=freqz(b,a);
subplot(2,2,3)
plot(w/pi,abs(H));
xlabel('\Omega(\pi)');
ylabel('Magnitude');
title('|H(e^j^\Omega)|')
grid on
subplot(2,2,4)
plot(w/pi,angle(H)/pi);
xlabel('\Omega(\pi)');
ylabel('Phase(\pi)');
title('\theta(\Omega)');
grid on
改变b,a的值得到不同表达式的结果。
对 H ( z ) = z 2 + 2 z + 1 z 3 − 0.5 z 2 − 0.005 z + 0.3 H(z) = \frac{{{z^2} + 2z + 1}}{{{z^3} - 0.5{z^2} - 0.005z + 0.3}} H(z)=z3−0.5z2−0.005z+0.3z2+2z+1,结果如下:

从单位冲激响应图可以看出,系统稳定。
对 H ( z ) = z 3 − z 2 + 2 3 z 4 + 3 z 3 − z 2 + 3 z − 1 H(z) = \frac{{{z^3} - {z^2} + 2}}{{3{z^4} + 3{z^3} - {z^2} + 3z - 1}} H(z)=3z4+3z3−z2+3z−1z3−z2+2,结果如下:

从单位冲激响应图可以看出,系统不稳定。
(2)
已知离散时间系统系统函数的零点z和极点p分别为:
- z=0,p=0.25
- z=0,p=1
- z=0,p=-0.25
- z=0, p 1 = 0.8 e j π 6 p_{1}=0.8{e^{j\frac{\pi }{6}}} p1=0.8ej6π, p 2 = 0.8 e − j π 6 p_{2}=0.8{e^{-j\frac{\pi }{6}}} p2=0.8e−j6π
- z=0, p 1 = e j π 8 p_{1}={e^{j\frac{\pi }{8}}} p1=ej8π, p 2 = e − j π 8 p_{2}={e^{-j\frac{\pi }{8}}} p2=e−j8π
- z=0, p 1 = 1.2 e j 3 π 4 p_{1}=1.2{e^{j\frac{3\pi }{4}}} p1=1.2ej43π, p 2 = 1.2 e − j 3 π 4 p_{2}=1.2{e^{-j\frac{3\pi }{4}}} p2=1.2e−j43π
试用MATLAB绘制上述6种不同情况下,系统函数的零极点分布图,并绘制相应单位抽样响应的时域波形,观察分析系统函数极点位置对单位抽样响应时域特性的影响和规律.
编写代码如下:
clc
clear;
close all;
z = 0;
p = [1]';
subplot(2,1,1)
zplane(z,p);
subplot(2,1,2)
b = poly(z);
a = poly(p);
impz(b,a);
改变p的值得到不同的结果。
当z=0,p=0.25:

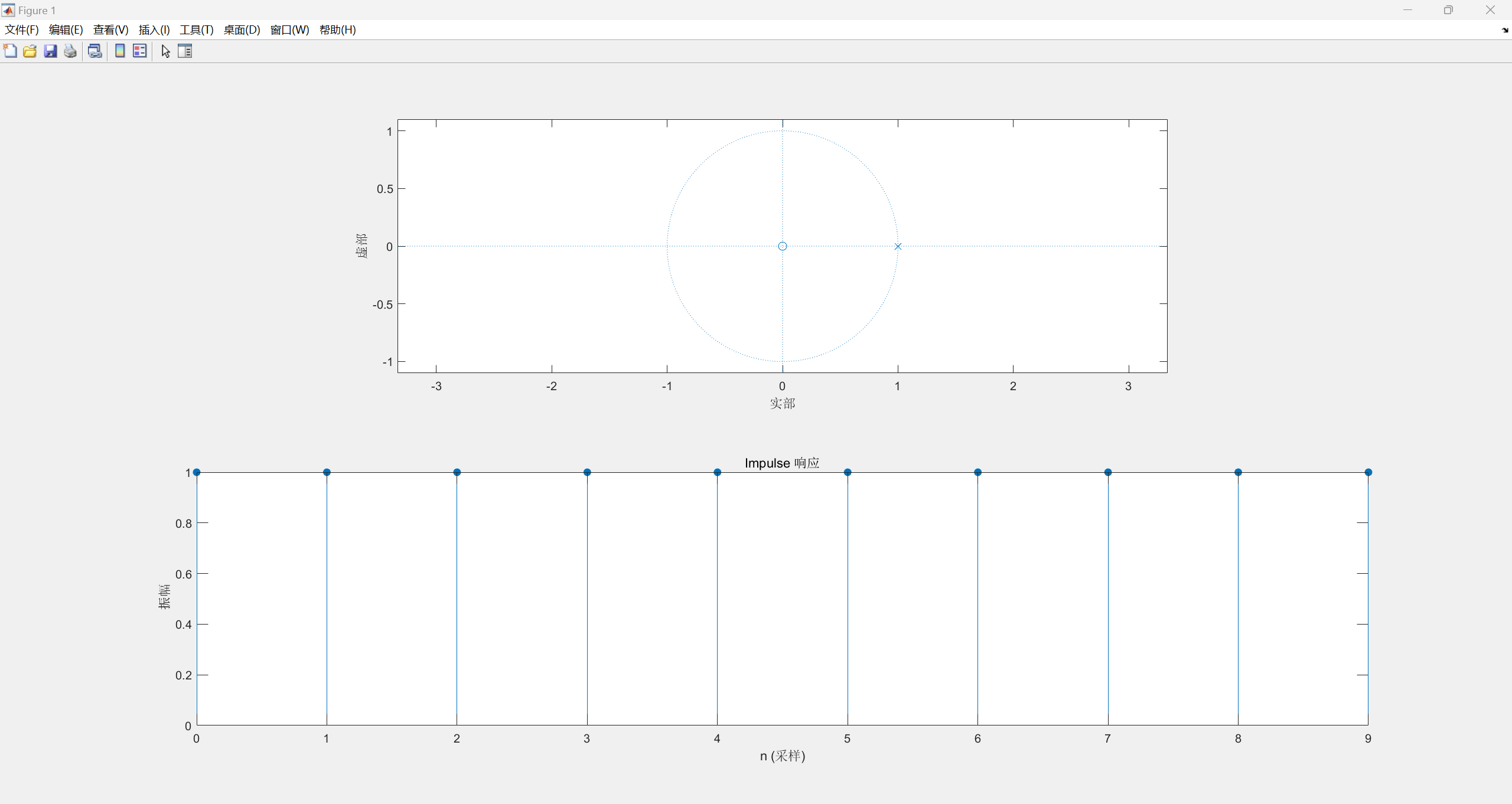
当z=0,p=1:
当z=0,p=-0.25:

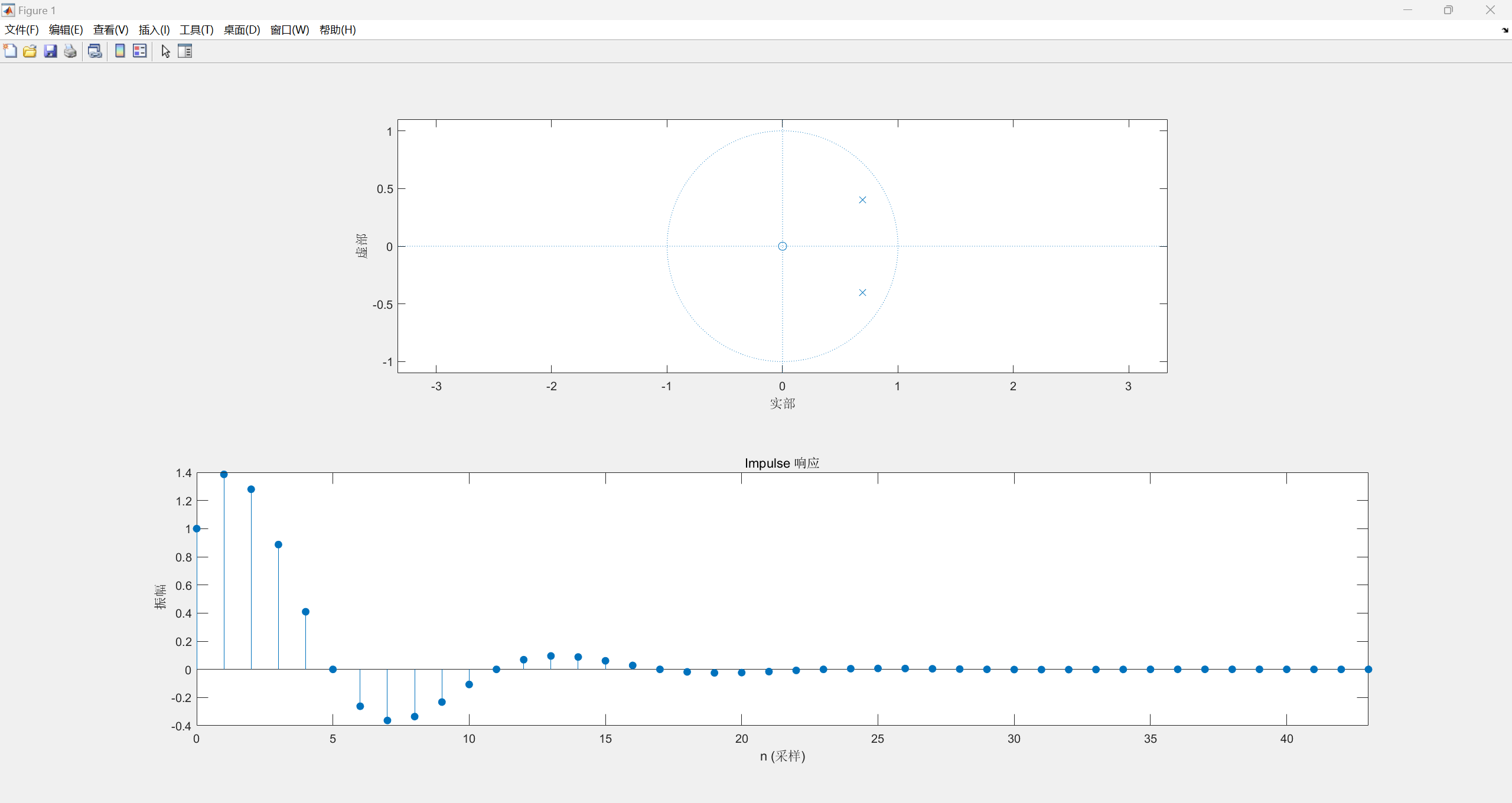
当z=0, p 1 = 0.8 e j π 6 p_{1}=0.8{e^{j\frac{\pi }{6}}} p1=0.8ej6π, p 2 = 0.8 e − j π 6 p_{2}=0.8{e^{-j\frac{\pi }{6}}} p2=0.8e−j6π:
当z=0, p 1 = e j π 8 p_{1}={e^{j\frac{\pi }{8}}} p1=ej8π, p 2 = e − j π 8 p_{2}={e^{-j\frac{\pi }{8}}} p2=e−j8π:
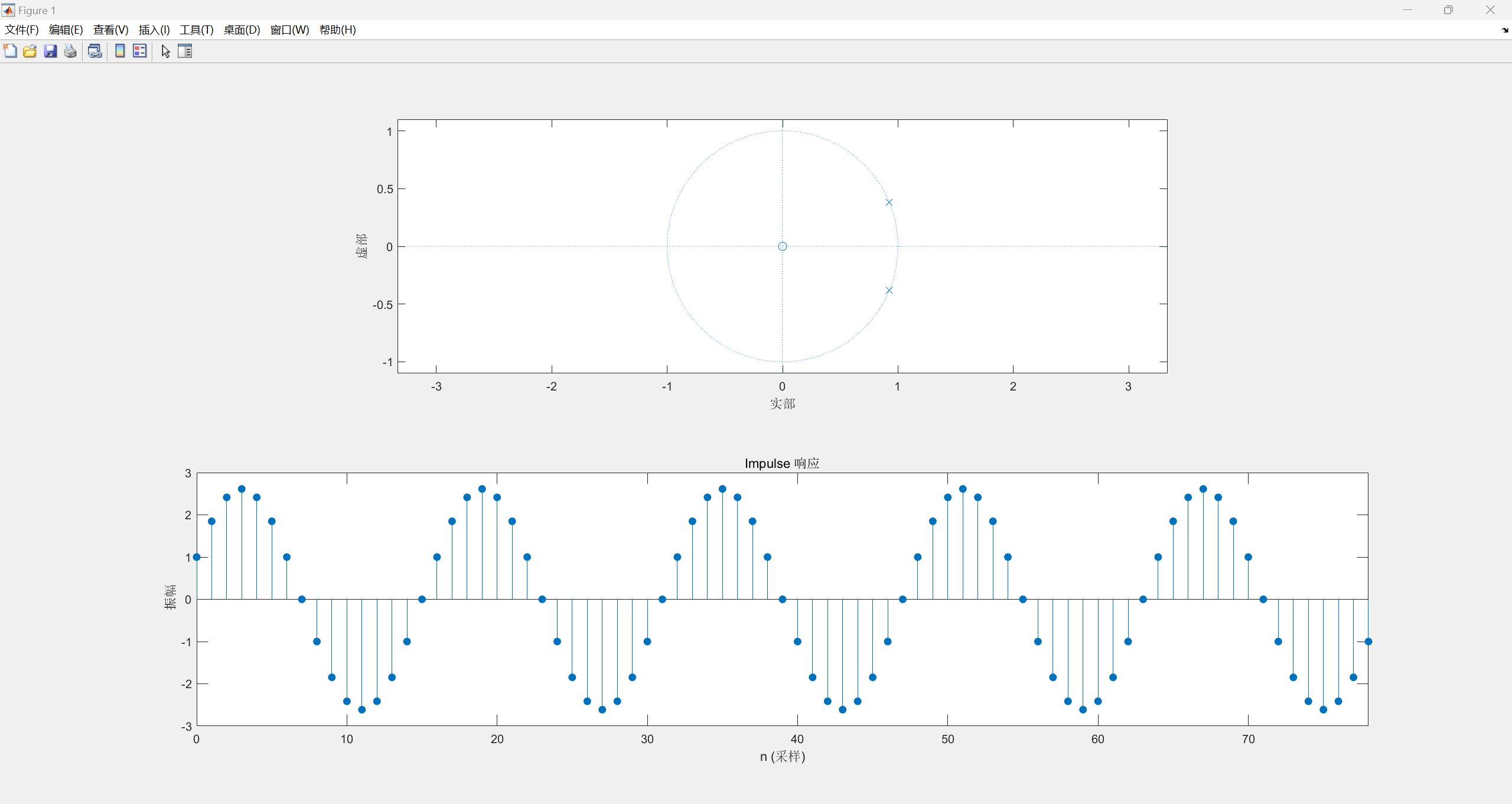
当z=0, p 1 = 1.2 e j 3 π 4 p_{1}=1.2{e^{j\frac{3\pi }{4}}} p1=1.2ej43π, p 2 = 1.2 e − j 3 π 4 p_{2}=1.2{e^{-j\frac{3\pi }{4}}} p2=1.2e−j43π:
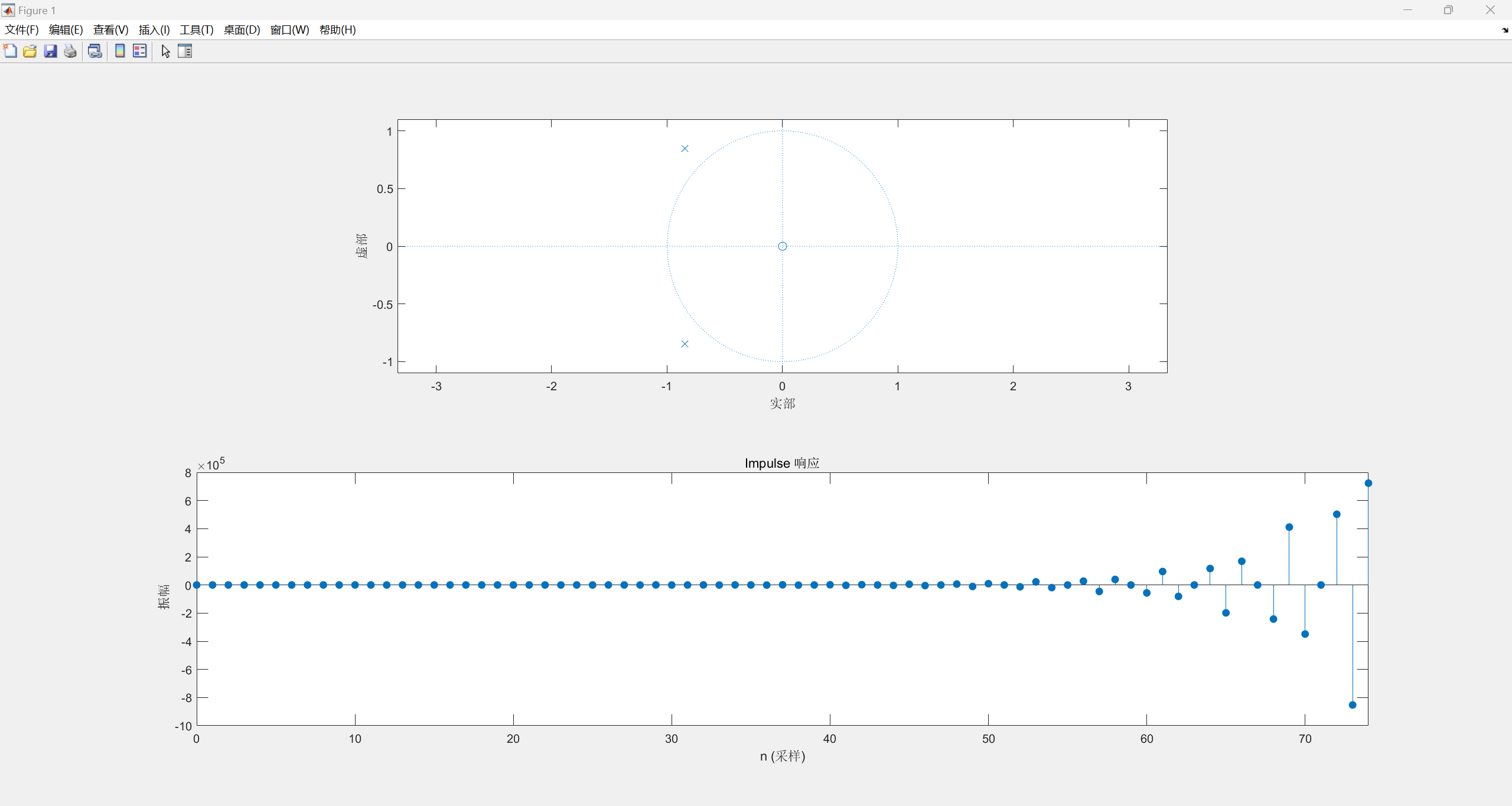
观察上述图像可以发现,当极点位于单位圆内,单位抽样序列收敛,绝对可和,当极点在单位圆上,单位抽样序列不收敛也不发散;当极点在单位圆外,单位抽样序列发散。
(3)
已知离散时间系统的系统函数分别为:
- H ( z ) = z ( z + 2 ) ( z − 0.8 e j π 6 ) ( z − 0.8 e − j π 6 ) H(z) = \frac{{z(z + 2)}}{{(z - 0.8{e^{j\frac{\pi }{6}}})(z - 0.8{e^{ - j\frac{\pi }{6}}})}} H(z)=(z−0.8ej6π)(z−0.8e−j6π)z(z+2)
- H ( z ) = z ( z − 2 ) ( z − 0.8 e j π 6 ) ( z − 0.8 e − j π 6 ) H(z) = \frac{{z(z - 2)}}{{(z - 0.8{e^{j\frac{\pi }{6}}})(z - 0.8{e^{ - j\frac{\pi }{6}}})}} H(z)=(z−0.8ej6π)(z−0.8e−j6π)z(z−2)
上述两个系统具有相同的极点,只是零点不同试用MATLAB分别绘制上述两个系统的零极点分布图及相应单位抽样响应的时域波形,观察分析系统函数零点位置对单位抽样响应时域特性的影响。
编写代码如下:
clc
clear;
close all;
z = [0 2]';
p = [0.8*exp(1i*pi/6) 0.8*exp(-1i*pi/6)]';
subplot(2,1,1)
zplane(z,p);
subplot(2,1,2)
b = poly(z);
a = poly(p);
impz(b,a);
改变z和p的值得到不同结果。
对于 H ( z ) = z ( z + 2 ) ( z − 0.8 e j π 6 ) ( z − 0.8 e − j π 6 ) H(z) = \frac{{z(z + 2)}}{{(z - 0.8{e^{j\frac{\pi }{6}}})(z - 0.8{e^{ - j\frac{\pi }{6}}})}} H(z)=(z−0.8ej6π)(z−0.8e−j6π)z(z+2),结果如下:

对于 H ( z ) = z ( z − 2 ) ( z − 0.8 e j π 6 ) ( z − 0.8 e − j π 6 ) H(z) = \frac{{z(z - 2)}}{{(z - 0.8{e^{j\frac{\pi }{6}}})(z - 0.8{e^{ - j\frac{\pi }{6}}})}} H(z)=(z−0.8ej6π)(z−0.8e−j6π)z(z−2),结果如下:

观察上述图像可得,零极点正负的改变会导致单位抽样响应波形沿x轴的翻转,翻转前后各点的值不变。
四、心得体会
通过本次实验,我系统且具体地了解了离散时间系统的z域分析,这对我对这方面的学习有很大帮助。
)
已知离散时间系统系统函数的零点z和极点p分别为:
- z=0,p=0.25
- z=0,p=1
- z=0,p=-0.25
- z=0, p 1 = 0.8 e j π 6 p_{1}=0.8{e^{j\frac{\pi }{6}}} p1=0.8ej6π, p 2 = 0.8 e − j π 6 p_{2}=0.8{e^{-j\frac{\pi }{6}}} p2=0.8e−j6π
- z=0, p 1 = e j π 8 p_{1}={e^{j\frac{\pi }{8}}} p1=ej8π, p 2 = e − j π 8 p_{2}={e^{-j\frac{\pi }{8}}} p2=e−j8π
- z=0, p 1 = 1.2 e j 3 π 4 p_{1}=1.2{e^{j\frac{3\pi }{4}}} p1=1.2ej43π, p 2 = 1.2 e − j 3 π 4 p_{2}=1.2{e^{-j\frac{3\pi }{4}}} p2=1.2e−j43π
试用MATLAB绘制上述6种不同情况下,系统函数的零极点分布图,并绘制相应单位抽样响应的时域波形,观察分析系统函数极点位置对单位抽样响应时域特性的影响和规律.
编写代码如下:
clc
clear;
close all;
z = 0;
p = [1]';
subplot(2,1,1)
zplane(z,p);
subplot(2,1,2)
b = poly(z);
a = poly(p);
impz(b,a);
改变p的值得到不同的结果。
当z=0,p=0.25:

当z=0,p=1:
当z=0,p=1:

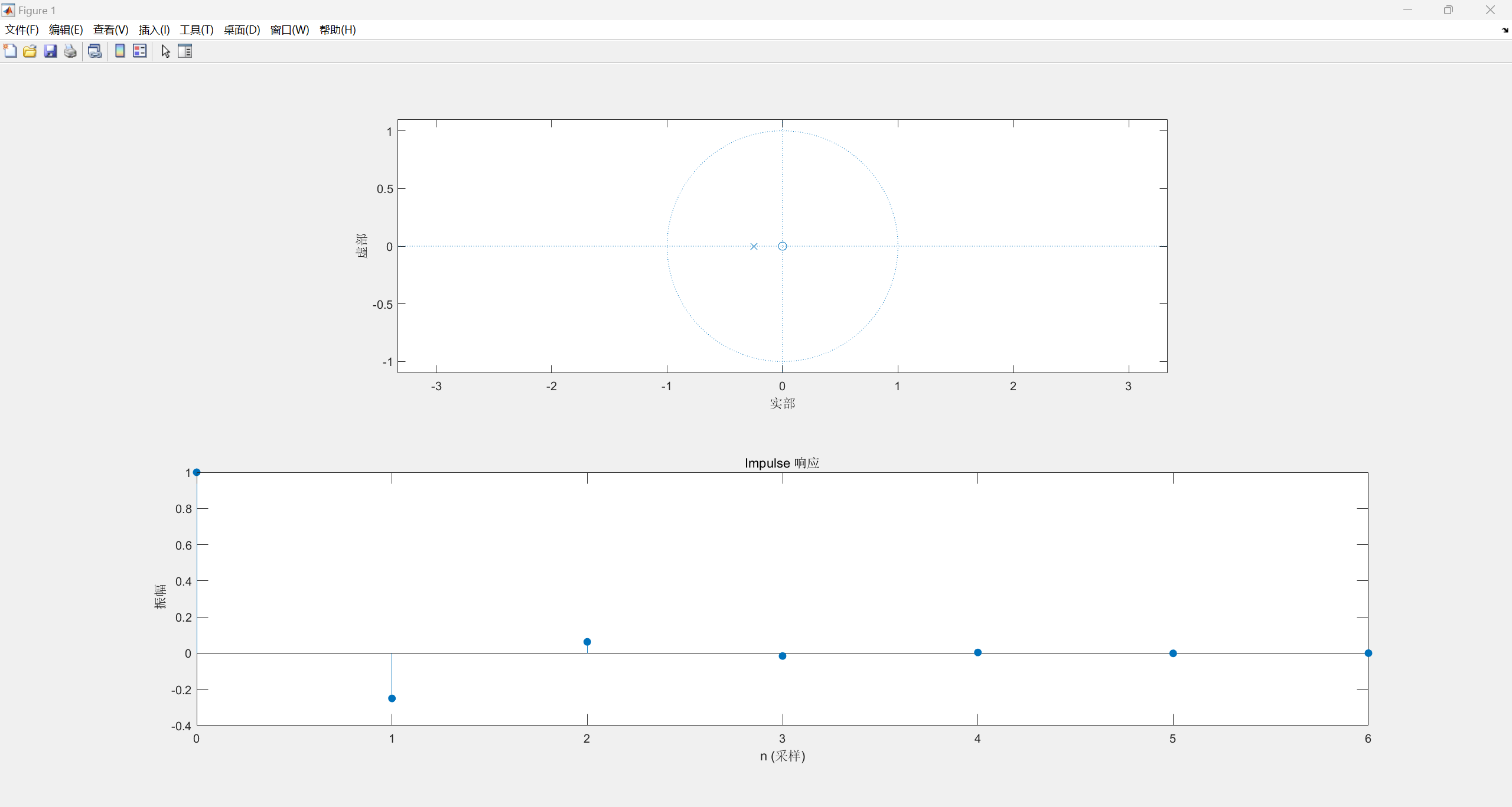
当z=0,p=-0.25:
当z=0, p 1 = 0.8 e j π 6 p_{1}=0.8{e^{j\frac{\pi }{6}}} p1=0.8ej6π, p 2 = 0.8 e − j π 6 p_{2}=0.8{e^{-j\frac{\pi }{6}}} p2=0.8e−j6π:

当z=0, p 1 = e j π 8 p_{1}={e^{j\frac{\pi }{8}}} p1=ej8π, p 2 = e − j π 8 p_{2}={e^{-j\frac{\pi }{8}}} p2=e−j8π:

当z=0, p 1 = 1.2 e j 3 π 4 p_{1}=1.2{e^{j\frac{3\pi }{4}}} p1=1.2ej43π, p 2 = 1.2 e − j 3 π 4 p_{2}=1.2{e^{-j\frac{3\pi }{4}}} p2=1.2e−j43π:

观察上述图像可以发现,当极点位于单位圆内,单位抽样序列收敛,绝对可和,当极点在单位圆上,单位抽样序列不收敛也不发散;当极点在单位圆外,单位抽样序列发散。
(3)
已知离散时间系统的系统函数分别为:
- H ( z ) = z ( z + 2 ) ( z − 0.8 e j π 6 ) ( z − 0.8 e − j π 6 ) H(z) = \frac{{z(z + 2)}}{{(z - 0.8{e^{j\frac{\pi }{6}}})(z - 0.8{e^{ - j\frac{\pi }{6}}})}} H(z)=(z−0.8ej6π)(z−0.8e−j6π)z(z+2)
- H ( z ) = z ( z − 2 ) ( z − 0.8 e j π 6 ) ( z − 0.8 e − j π 6 ) H(z) = \frac{{z(z - 2)}}{{(z - 0.8{e^{j\frac{\pi }{6}}})(z - 0.8{e^{ - j\frac{\pi }{6}}})}} H(z)=(z−0.8ej6π)(z−0.8e−j6π)z(z−2)
上述两个系统具有相同的极点,只是零点不同试用MATLAB分别绘制上述两个系统的零极点分布图及相应单位抽样响应的时域波形,观察分析系统函数零点位置对单位抽样响应时域特性的影响。
编写代码如下:
clc
clear;
close all;
z = [0 2]';
p = [0.8*exp(1i*pi/6) 0.8*exp(-1i*pi/6)]';
subplot(2,1,1)
zplane(z,p);
subplot(2,1,2)
b = poly(z);
a = poly(p);
impz(b,a);
改变z和p的值得到不同结果。
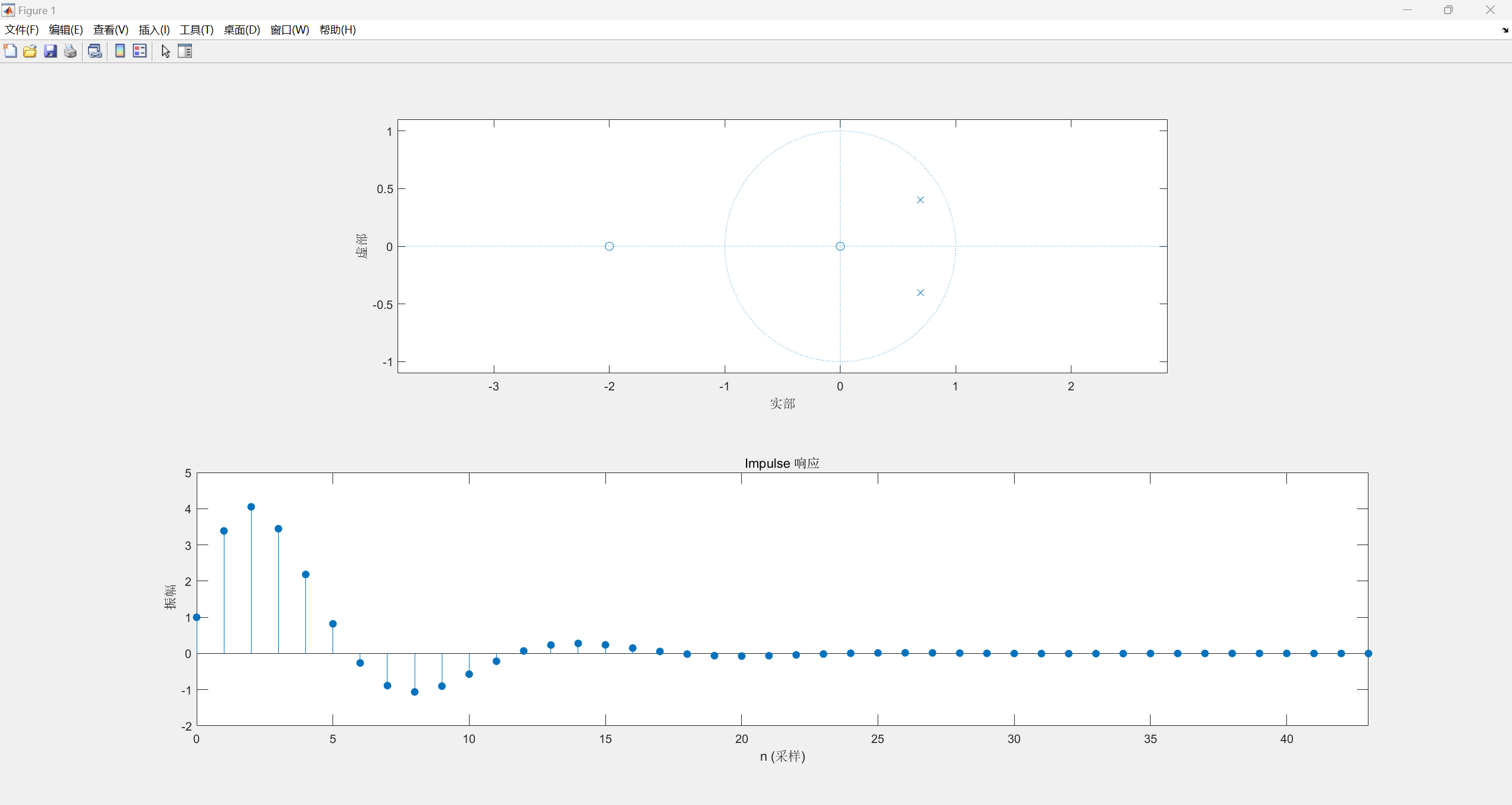
对于 H ( z ) = z ( z + 2 ) ( z − 0.8 e j π 6 ) ( z − 0.8 e − j π 6 ) H(z) = \frac{{z(z + 2)}}{{(z - 0.8{e^{j\frac{\pi }{6}}})(z - 0.8{e^{ - j\frac{\pi }{6}}})}} H(z)=(z−0.8ej6π)(z−0.8e−j6π)z(z+2),结果如下:
对于 H ( z ) = z ( z − 2 ) ( z − 0.8 e j π 6 ) ( z − 0.8 e − j π 6 ) H(z) = \frac{{z(z - 2)}}{{(z - 0.8{e^{j\frac{\pi }{6}}})(z - 0.8{e^{ - j\frac{\pi }{6}}})}} H(z)=(z−0.8ej6π)(z−0.8e−j6π)z(z−2),结果如下:

观察上述图像可得,零极点正负的改变会导致单位抽样响应波形沿x轴的翻转,翻转前后各点的值不变。























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








